Circuiti sequenziali: flip-flop e alee

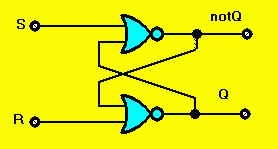
 É il tipo più semplice di circuito sequenziale. Una realizzazione in logica NOR é rappresentata in figura:

Non sapendo di aver a che fare con un circuito sequenziale, potremmo provare a studiare il comportamento del circuito illustrato in figura ricavandone la tavola di verità. Questo approccio é applicabile solo per tre delle quattro possibili configurazioni di valori in ingresso:

In particolare il valore di uscita corrispondente alla configurazione di ingresso S=R=0 non é determinabile a causa del ciclo chiuso tra ingressi e uscite delle funzioni.

L'analisi può procedere solo se supponiamo di conoscere già il valore dell'uscita Q quando entrambi gli ingressi assumono il valore 0. Se ipotizziamo Q=0, allora possiamo vedere che questo implica valore 1 in uscita alla funzione NOR in alto, e di conseguenza Q=0, confermando la nostra ipotesi. Ma anche se ipotizziamo Q=1 possiamo concludere che questo implica valore 0 in uscita alla funzione NOR in alto, e di conseguenza Q=1, confermando la nostra ipotesi di partenza. Troviamo quindi un caso in cui la soluzione al problema di trovare il valore di uscita non é unica: entrambe le soluzioni Q=0 e Q=1 sono ammissibili con la configurazione di ingresso S=R=0.

Come possiamo arrivare a determinare il valore in uscita nel caso in cui entrambi i valori booleani sono soluzioni ammissibili? La risposta consiste nel considerare sequenze di configurazioni diverse, facendo variare nel tempo il valore delle variabili di ingresso.

Supponiamo di partire dalla configurazione S=1 ed R=0, e di cambiare poi il valore di S portandolo a 0. Siccome le nostre funzioni NOR saranno realizzate mediante dispositivi fisici, possiamo pensare che qualsiasi realizzazione del nostro flip-flop sarà sempre soggetta ad una certa "inerzia" dei valori di uscita rispetto a cambiamenti dei valori di ingresso. Osservando il comportamento del flip-flop con una scala dei tempi sufficientemente fine potremo sempre individuare un intervallo di tempo non nullo durante il quale i valori di uscita non cambiano nonostante una variazione dei valori di ingresso sia gia avvenuta. Nel nostro caso specifico, riusciremo sempre ad individuare un intervallo di tempo finito durante il quale il valore dell'uscita Q continua ad essere 1 anche dopo che il valore della variabile di ingresso S é diventato 0; durante tale intervallo di tempo la funzione OR in alto continua a produrre il valore di uscita 0, che conferma il valore Q=1 in uscita alla funzione NOR in basso. Quindi, per una forma di continuità dei valori in uscita alle funzioni a seguito di variazioni dei valori in ingresso, possiamo affermare con certezza che Q deve continuare ad assumere sempre il valore 1 anche dopo che l'ingresso S ha assunto il valore 0.  

In modo del tutto analogo possiamo arrivare alla conclusione che se la configurazione di ingresso S=R=0 é preceduta nel tempo dalla configurazione S=0 ed R=1 (che forza in uscita il valore Q=0 senza ambiguità), allora in uscita troveremo sicuramente il valore Q=0.

Possiamo quindi toccare con mano una proprietà che distingue nettamente i circuiti sequenziali dai circuiti combinatori: in un circuito combinatorio il valore delle uscite é univocamente determinato dai valori attuali delle variabili di ingresso (a meno di un piccolo ritardo dovuto all'inerzia di assestamento dei dispositivi fisici che realizzano le funzioni); in un circuito sequenziale, il valore delle uscite può dipendere, oltre che dai valori attuali, anche dalla sequenza dei valori precedenti delle variabili di ingresso.

Notiamo infine che la configurazione di ingresso S=R=1 é anomala dal punto di vista di uso del circuito sequenziale: la sequenza S=R=1 seguito da S=R=0 non determina univocamente il valore dell'uscita Q (in alcuni casi potrebbe generare delle oscillazioni periodiche tra i valori Q=0 e Q=1, con un periodo determinato dal tempo di assestamento dei dispositivi che realizzano le funzioni NOR). Per questo la configurazione di ingresso S=R=1 non viene normalmente utilizzata. Vediamo quali vantaggi porta l'utilizzazione di circuiti sincroni rispetto a quella dei circuiti asincroni, a fronte della maggior complessità di realizzazione.

Consideriamo l'esempio di circuito sequenziale asincrono illustrato in figura:

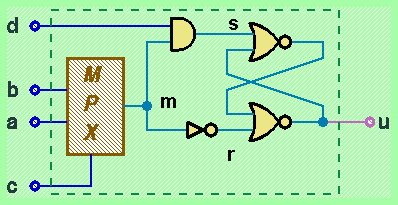
Supponiamo di voler determinare il valore dell'uscita u dopo aver applicato sugli ingressi la seguente sequenza di combinazioni di valori:

Dalla tavola di verità delle funzioni combinatorie e dalla descrizione del flip-flop Set/Reset determiniamo che la prima configurazione memorizza il valore u=1. La seconda configurazione consente al flip-flop di mantenere il valore precedentemente memorizzato, così come la terza. Quindi possiamo dedurre che il valore prodotto in uscita dall'applicazione della sequenza di ingressi considerata sia u=1.  

Non soddisfatti di questa risposta, proviamo ora a considerare alcuni dettagli realizzativi del dispositivo Multiplexer. Supponendo di considerare la realizzazione minimale del multiplexer vista in precedenza mediante un NOT, due AND ed un OR, la cui rappresentazione grafica risulta la seguente

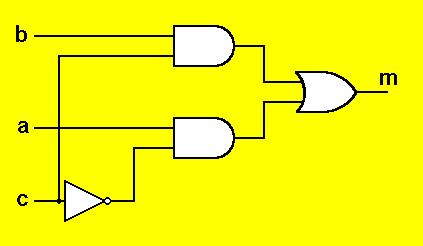
possiamo ipotizzare che ciascuna funzione logica elementare sia caratterizzata da un ritardo di una unità di tempo per produrre il corretto valore di uscita a fronte di una variazione dei valori di ingresso. Il passaggio dalla seconda alla terza configurazione della sequenza può quindi essere decomposto in passi elementari di durata pari ad una unità di tempo:

1.appena cambiata la configurazione di ingresso nessuna funzione cambia uscita: l'AND in alto e l'OR mantengono il valore 1, l'AND in basso ed il NOT mantengono il valore 0;

2.dopo una unità di tempo l'AND in alto passa al valore 0 (come dettato dalla sua tavola di verità) e il NOT passa al valore 1, mentre l'OR mantiene 1 e l'AND in basso mantiene 0;

3.dopo due unità di tempo l'OR passa al valore 0, mentre l'AND in basso passa al valore 1 e NOT ed AND in alto mantengono il valore raggiunto in precedenza;

4.dopo tre unità di tempo, l'OR torna nuovamente a 1, mentre le altre funzioni del multiplexer mantengono il valore del passo precedente.

Da questa analisi più dettagliata legata alle temporizzazioni dei dispositivi costituenti il Multiplexer, vediamo quindi che questo nel transitorio di passaggio dalla seconda configurazione di ingresso alla terza (entrambe con valore di uscita 1 per il Multiplexer) può generare per un breve tempo una situazione intermedia, detta alea di commutazione, con uscita 0. Tale alea di commutazione del multiplexer può determinare la commutazione del flip-flop al valore u=0.

Questo esempio ci mostra come possa essere difficile prevedere il risultato in uscita di un circuito combinatorio a seguito di variazioni delle configurazioni in ingresso. In particolare vediamo come anche alee molto brevi possono determinare la commutazione permanente di un flip-flop rispetto al valore di uscita previsto basandosi sulla specifica del circuito combinatorio data sotto forma di tavola di verità (prescindendo quindi dalle temporizzazioni delle funzioni).

Il problema di "imprevisti" dovuti ad alee di commutazione può essere completamente eliminato in circuiti di tipo sincrono mediante un'opportuna utilizzazione della variabile di controllo clock.

Per meglio visualizzare il problema si suggerisce di creare un'entita' alea come nella seconda figura, la cui interfaccia e':

entity alea is

port (c,a,b,d: in bit; u: out bit);

end alea;

Consideriamo ora l' esempio precedente utilizzando pero' componenti piu' veloci (aventi un ritardo di propagazione di 100 ps) e un flip-flop di tipo D (detto anche latch) attivato su livello alto (level triggered).

Questo puo' indurre a pensare che con un segnale a livello di abilitazione si possano risolvere tutti i problemi; in realta' non e' ancora sufficiente.

Si consideri infatti una serie di latch di tipo D con enable collegati in cascata tra di loro come rappresentato nella seguente figura:

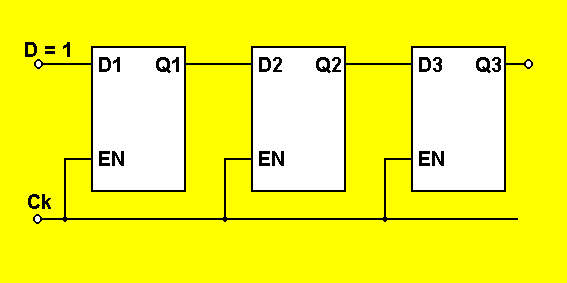
Il latch di tipo D con enable e' tale per cui la sua tabella risulta:

Una soluzione sembrerebbe quella di abilitare i latch per un tempo brevissimo, inferiore al tempo di propagazione del latch stesso, utilizzando segnali di clock con duty cycle ridottissimo (in altre parole, rispetto al periodo del clock, la percentuale di tale periodo in cui il segnale rimane alto deve essere breve). Impulsi tanto brevi non sono generalmente in grado di garantire corrette commutazioni dei latch; la trasmissione in un sistema digitale d'implusi cosi' rapidi e' difficilmente realizzabile e poco affidabile.

La soluzione corretta e' pertanto quella di impiegare dei dispositivi in cui la commutazione delle uscite, benche' determinata dallo stato degli ingressi e della eventuale situazione precedente delle uscite, avviene SOLO in sincronismo con una ben precisa transizione del segnale di clock.

Puo' risultare un utile esercizio ricavare lo schema circuitale del flip-flop S-R con enable e del latch sia level che edge triggered, partendo dall'analisi dei file .vhd relativi.