Settima esercitazione
Esercizio 1
Esercizio 2
Esercizi di calcolo numerico
Svolgete il primo esercizio ed uno a scelta tra il secondo ed il terzo
In ogni esercizio fate anche il grafico delle funzioni che utilizzate.
Esercizio 1
Calcolate l'integrale definito di una funzione utilizzando il metodo dei trapezi ed il metodo di Simpson
e confrontatene la precisione a numero di intervalli N fissato. (N+1 punti)
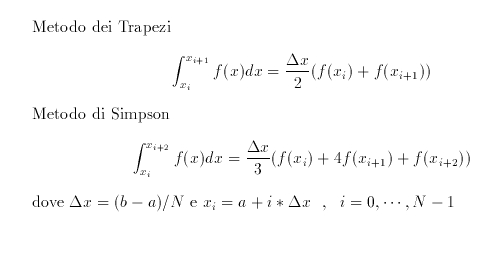
La funzione che calcola l'integrale dovrà avere, per entrambi i metodi, il prototipo
double integrale(double f(double), double xmin, double xmax, int n)
dove l'intero n definisce il numero di campionamenti e quindi la precisione dell'integrale.
Provate le routines su una funzione di cui sia noto l'integrale (a vostra scelta) e sulla funzione
gauss.cpp con estremi di integrazione xmin = -1 e xmin = +1
Facoltativo: creare anche una funzione che calcoli l'integrale con precisione data:
l'integrale viene ripetuto, dimezzando ogni volta n, finché la variazione
tra i valori dell'integrale in due iterazioni successive è minore della precisione.
Il prototipo della funzione sarà del tipo
double integrale_pre(double f(double), double xmin, double xmax, double prec)
e dovrà fare uso delle funzioni predentemente definite.
Esercizio 2
Trovare lo zero di una funzione nell'intervallo [xmin,xmax] tale che
xmin*xmax<0 (si suppone che l'intervallo contenga un solo zero)
Il metodo consiste in
- definire un passo (spostamento lungo l'asse x);
- partendo da uno dei due estremi valutare la funzione in punti
successivi (la distanza tra i punti è il passo)
fino a quando la funzione non cambia segno;
- dimezzare il passo e ripetere il punto precedente,
cambiando direzione lungo l'asse x, fincheé il passo è superiore
alla precisione voluta.
Il metodo ha massima efficienza se il valore iniziale del passo è
uguale a metà intervallo (metodo di bisezione).
Il prototipo della funzione sarà del tipo
double zeri(double f(double), double xmin, double xmax, double prec)
e dovrà ritornare la coordinata x dello zero trovato.
Provate la routine su una funzione di cui conoscete lo zero
e per risolvere l'equazione xex=cos(x) in [-1,1].