NOTA PRELIMINARE: La parte iniziale di questo materiale, e in particolare quello riguardante la rappresentazione di numeri fino ai codici binari posizionali, viene ora trattata nel corso di Informatica Generale. Tale parte viene mantenuta all'interno di queste dispense per completezza, e costituisce un prerequisito per i successivi argomenti effettivamente trattati all'interno del corso di Architettura dei Calcolatori.
Uno dei problemi fondamentali che incontriamo quando vogliamo usare un sistema di calcolo per manipolare delle informazioni é quello di rappresentare le informazioni stesse all'interno del sistema. Questo problema viene risolto in informatica mediante l'adozione di oppurtuni codici che stabiliscono una corrispondenza tra la "informazione" significativa per il problema (l'applicazione) che si sta considerando ed una serie di simboli manipolabili dal sistema. Nell'esempio della macchina di Von Neumann i simboli manipolabili dalla macchina sono numeri interi di valore non superiore ad una soglia prefissata, quindi ogni informazione deve essere codificata sotto tale forma per poter essere trattata dal sistema.
Possiamo pensare di dare una definizione "astratta" del concetto di codice, senza far riferimento a nessun esempio specifico. Poi però istanzieremo i problemi su una serie di esempi diversi per renderci conto che anche un concetto molto astratto e generale ci può aiutare molto a risolvere problemi concreti e specifici.
Sia X un qualsiasi insieme (finito o infinito), che rappresenta gli oggetti o le informazioni che vogliamo trattare.
Sia A un qualsiasi alfabeto finito di simboli (le 10 cifre arabe, oppure le 21 lettere dell'alfabeto italiano, oppure l'insieme dei tre colori rosso giallo e verde, non importa ...). Con A* indichiamo l'insieme di tutte le possibili sequenze (ordinate da sinistra a destra) di simboli dell'alfabeto A, di lunghezza finita e infinita, compresa la sequenza vuota (che non contiene nessun simbolo).
Definiamo una funzione iniettiva di codifica
cod: X -> A*
ed una relativa funzione di decodifica
decod: A* -> X U {errore}
tali che per ogni y appartenente ad X, decod(cod(y)) = y
L'insieme X, l'alfabeto A, e le funzioni cod e decod formano
un Codice per la rappresentazione di elementi di X.
La sequenza di simboli cod(y) corrispondente ad un qualsiasi elemento
y appartenente ad X
verrà chiamata "codifica di y" (ovvero "rappresentazione di y")
(secondo il codice considerato).
Normalmente non tutte le sequenze di simboli b appartenenti ad A*
saranno rappresentazioni di elementi appartenenti ad X.
Solitamente, anzi, in Informatica avremo a che fare con codici
a lunghezza fissa,
nei quali é predeterminato il numero di simboli che
costituiscono una codifica corretta, e tutte le altre sequenze
(che ovviamente darebbero decod(b)= errore) non vengono neanche
prese in considerazione.
Cominciamo quindi a trattare il caso semplice della rappresentazione dei numeri naturali 0, 1, 2, ..., ecc. Può sembrare un problema di scarsa rilevanza, visto che viene insegnato ai bambini della scuola elementare. In realtà non vogliamo verificare se ci ricordiamo le nozioni apprese alla scuola elementare, ma piuttosto provare a riflettere sul metodo seguito per arrivare a definire un codice di rappresentazione "conveniente" per un essere umano e cercare di capire in quale misura metodi analoghi ci possono portare a definire codici di rappresentazione "convenienti" per un sistema di calcolo; partiamo infatti dal presupposto che una tecnica conveniente per un bambino di 6 anni non sia necessariamente conveniente per un sistema di calcolo e viceversa.
In effetti bisogna stabilire quali sono gli usi per i quali un codice di rappresentazione viene proposto. Se l'unico scopo é quello di scrivere un numero su un pezzo di carta e poi poterlo rileggere, potremmo pensare di ottimizzare la superficie di carta occupata da un simbolo, in modo da intaccare il meno possibile l'equilibrio ecologico delle foreste che ci forniscono la materia prima per produrre carta. Se invece pensiamo di utilizzare la rappresentazione scritta dei numeri per sviluppare degli algoritmi di calcolo (per esempio somma tra due numeri), allora il criterio principale diventerà quello di semplificare al massimo tale operazione, in modo da limitare per quanto possibile sia il tempo per arrivare a produrre il risultato, sia la probabilità di commettere errori di calcolo. Se vogliamo poi proporre un codice "di uso generale", ovvero usare sempre lo stesso codice per tante esigenze diverse, allora dovremo necessariamente cercare un codice di "compromesso" che non sia "troppo peggio" di altri per nessuna delle applicazioni più frequenti.
Ovviamente, le considerazioni generali che facciamo qui sui codici di rappresentazione dei numeri vanno intese come esempi di problemi. La rappresentazione di numeri all'interno di un sistema di calcolo é ormai altrettanto consolidata quanto l'uso del sistema decimale posizionale con cifre arabe insegnato alle elementari, tanto é vero che esistono degli standard internazionali (esempio) ormai seguiti da tutti i produttori di sistemi. Quindi nel futuro della vita professionale di un informatico nessuno verrà mai a chiedergli di inventare un nuovo codice per la rappresentazione di numeri. Tuttavia il problema si presenta abbastanza spesso per la rappresentazione di altri tipi di informazioni, per cui é importante acquisire una capacità critica e di riflessione su questa classe di problemi.
Facciamo finta di non conoscere (o di aver dimenticato) la rappresentazione decimale posizionale dei numeri a cui siamo così tanto abituati. Un'altra rappresentazione di numeri che tutti noi italiani dovremmo conoscere (ma che non usiamo quasi mai) é quella romana.
Facciamo un breve ripasso di tale rappresentazione.
Viene usato un alfabeto di sette simboli:
I V X L C D M
che rappresentano rispettivamente i numeri uno, cinque, dieci, cinquanta, cento,
cinquecento e mille.
Tali sette numeri "privilegiati" vengono rappresentati mediante un solo
simbolo, mentre tutti gli altri numeri vengono rappresentati mediante la
combinazione di due o più simboli allineati su una riga orizzontale,
seguendo un algoritmo abbastanza complesso.
Il criterio ispiratore di tale algoritmo di codifica (che prevede una rappresentazione unica per ogni numero) é quello di minimizzare il numero di occorrenze di simboli utilizzati. Ricordiamo che il numero "due" viene rappresentato con due occorrenze del simbolo usato per rappresentare "uno" (ovvero II), ed il numero "tre" viene rappresentato da tre occorrenze del simbolo usato per rappresentare "uno" (ossia III). Per il numero cinque si sarebbe potuto utilizzare lo stesso metodo (ossia rappresentarlo con IIIII), ma questo avrebbe richiesto l'uso di cinque occorrenze, mentre l'uso del simbolo associato al cinque (ossia V) permette di rappresentare il numero con una sola occorrenza. Il modo "strano" di rappresentare il numero "quattro" (ossia IV) dando il significato di sottrazione all'ordinamento di un simbolo di valore inferiore precedente un simbolo di valore superiore é una astuzia per ridurre a due il numero di occorrenze rispetto alla ovvia rappresentazione IIII che invece ne richiederebbe quattro.
Tra i maggiori difetti (dal nostro punto di vista) della rappresentazione
romana dei numeri, vi é quello di mancanza di uniformità
dell'algoritmo per numeri di valore maggiore o uguale a quattromila, dovuta alla
mancanza di simboli unici per la rappresentazione di cinquemila, diecimila,
cinquantamila, ecc.
Questo ci costringe, per esempio a rappresentare il numero cinquantamila mediante
cinquanta occorrenze del simbolo M, un vero attentato alle capacità cognitive
di qualunque persona umana: chi riuscirebbe mai "a colpo d'occhio"
a riconoscere se nella seguente rappresentazione ci sono cinquanta o quarantanove
o cinquantuno occorrenze?
MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM
(in effetti questa é la rappresentazione romana di quarantaseimila,
contare per credere!).
Ovviamente potremmo sempre pensare di usare un alfabeto con un numero di simboli
maggiore di sette, ma se rimaniamo nell'ambito degli alfabeti finiti (chi di noi
potrebbe mai imparare un alfabeto infinito?) non faremmo che spostare
la soglia del problema ad un valore un po' più alto.
Tra i maggiori pregi della rappresentazione romana, possiamo invece notare la facilità con coi vengono rappresentati numeri "arrotondati" ai numeri fondamentali rispetto a numeri arbitrari, indipendentemente dal loro valore. Questo in un certo senso corrisponde alle nostre capacità cognitive: per noi é sicuramente più facile ricordare numeri come cinquecento, mille, millecinquecento (in romano D, M, MD) piuttosto che quattrocentoquarantotto, milleventiquattro, milleduecentottantuno (in romano CDXLVIII, MXXIV, MCCLXXXI). In oltre ricordare il numero mille non ci comporta difficoltà superiori rispetto al numero cento, o dieci. Provate a pronunciare tali numeri ad alta voce per convincervi che anche a livello verbale noi diamo la preferenza di una maggior sinteticità ai numeri arrotondati alle potenze di dieci. Tale corrispondenza non esiste invece nella rappresentazione decimale a cui siamo abituati da tanto tempo (448 e 500 sono entrambi rappresentati su tre cifre, mentre 1000 é rappresentato su quattro cifre, quindi implica una maggiore complessità di scrittura).
É inutile ricordare come rappresentiamo usualmente i numeri. Siamo talmente abituati a questa rappresentazione che spesso confondiamo la rappresentazione decimale posizionale di un numero con il "numero stesso" (ossia col concetto matematico di numerale).
Qualitativamente, il sistema decimale posizionale ha un vantaggio fondamentale rispetto al sistema romano per la rappresentazione di numeri molto grandi: il numero di cifre (ovvero di occorrenze di simboli dell'alfabeto, secondo la nostra terminologia informatica) cresce in modo logaritmico con il valore del numero da rappresentare, anziché in modo lineare. Uno svantaggio é quello di richiedere un numero di occorrenze di simboli identico per numeri dello stesso ordine di grandezza, indipendentemente dalla "regolarità" del numero che ci può facilitare o meno lo sforzo di memorizzazione.
Normalmente gli informatici non sono interessati solo agli aspetti di memorizzazione e lettura di informazioni, ma anche alla loro manipolazione. Nel caso di numeri, i tipi più semplici di manipolazione che possiamo incontrare sono le operazioni aritmetiche tra coppie di numeri.
Ovviamente le operazioni aritmetiche sono definite dal punto di vista matematico su dei "numeri astratti" indipendentemente dal fatto che questi vengano rappresentati con un codice piuttosto che un altro. Tuttavia quando vogliamo definire un algoritmo meccanizzabile per effettuare per esempio la somma, allora questo algoritmo deve operare su una rappresentazione concreta dei numerali che vogliamo sommare.
Il punto che vogliamo evidenziare qui é che la complessità dell'algoritmo di manipolazione dei dati (nel nostro esempio la somma) dipende dalla rappresentazione che stiamo utilizzando. Cambiando la rappresentazione possiamo ottenere algoritmi di manipolazione più o meno semplici e più o meno efficienti.
Per esempio, un algoritmo di somma tra due numeri che operasse sulla rappresentazione romana di numeri naturali risulterebbe estremamente complesso da concepire (oltre che inefficiente da eseguire). Non per nulla gli antichi inventarono l'abaco (pallottoliere) come metodo alternativo di rappresentazione dei numeri in grado di supportare un semplice ed efficace algoritmo di somma e di sottrazione. Quindi, se adottassimo ancora il metodo romano di scrittura dei numeri, dovremmo prima decodificare il numero trasformandolo in una equivalente rappresentazione su un abaco, poi effettuare l'operazione aritmetica richiesta, e infine ricodificare il risultato nel codice usato per la scrittura.
Il codice decimale posizionale, invece, ci consente di applicare un algoritmo di somma molto semplice ed efficace (di complessità logaritmica nel valore dei numeri trattati, così come il numero di cifre usate per la rappresentazione) che opera direttamente sulla codifica del numero producendo la codifica del risultato. Mediante l'uso della tavola Pitagorica possiamo in modo analogo sviluppare un algoritmo per la moltiplicazione. Algoritmi più o meno complessi operanti direttamente sulla rappresentazione sono in oltre conosciuti (e studiati a scuola) per la realizzazione delle operazioni di divisione, calcolo della radice quadrata, ecc. La disponibilità di questi algoritmi ha sicuramente contribuito in maniera decisiva alla "scelta" di questo metodo di rappresentazione rispetto alle tante altre alternative che uno potrebbe immaginare di adottare.
Tornando a considerare il problema di rappresentazione di numeri all'interno di un sistema di calcolo, la considerazione sulla possibilità di supportare efficacemente algoritmi di manipolazione diventa il criterio principale di scelta per un codice piuttosto di un altro, oltre alle caratteristiche di concisione della rappresentazione.
I vantaggi del sistema di rappresentazione decimale posizionale non derivano dal fatto di aver scelto un alfabeto di dieci simboli ("0", "1", "2", ... "9"), ma piuttosto dal modo di usare ed interpretare questi simboli per costruire le rappresentazioni dei numeri. Possiamo quindi generalizzare questo codice al caso di N (non necessariamente uguale a dieci) simboli diversi, mantenendo invariate tutte le altre regole di codifica.
Nel caso di alfabeto di due simboli (per esempio "0" e "1"), otteniamo la famigerata rappresentazione binaria, incubo di ogni informatico neofita. La i-esima cifra da destra verso sinistra rappresenta il coefficiente moltiplicativo della i-esima potenza di due (anziché di dieci) che compone il numero. Possiamo applicare tranquillamente gli algoritmi noti per la rappresentazione decimale di somma, differenza, moltiplicazione, divisione, ecc. alla rappresentazione binaria, semplicemente ricordandosi che "il riporto" viene generato al superamento della cifra "1" anziché "9". Il vantaggio di questa rappresentazione dal punto di vista informatico deriva da vincoli di tipo realizzativo dei dispositivi elettronici: dispositivi in grado di operare distinzioni e manipolazioni di due soli simboli (o meglio, grandezze elettromagnetiche) sono più facili da realizzare e meno costosi di dispositivi in grado di operare su un numero maggiore di simboli.
Ponendo N=8 oppure N=16 si ottengono i sistemi di numerazione ottale ed esadecimale. L'interesse informatico per questi codici deriva da una loro sostanziale omogeneità col sistema binario accoppiata ad una maggior concisione (in termini di numero di cifre utilizzate per rappresentare un determinato valore). In effetti, la conversione da binario ad ottale o esadecimale, e viceversa risulta essere particolarmente semplificata dal fatto che in entrambi i casi il numero di simboli é una potenza di due. Nel caso della rappresentazione ottale, per esempio, si può stabilire una corrispondenza tra terne di simboli della rappresentazione binaria e singoli simboli della rappresentazione ottale dello stesso numero; in questo senso, la rappresentazione ottale può essere vista come una pura e semplice abbreviazione della rappresentazione binaria, che sostituisce ad ogni terna di cifre binarie consecutive una sola cifra ottale.
Su carta noi siamo abituati ad applicare un principio di economicità della rappresentazione che ci porta a definire la regola: "non si scrive zero come cifra più a sinistra". In questo modo, oltre a risparmiare carta, otteniamo anche una rappresentazione unica per ogni numero. In mancanza di questa regola noi potremmo scrivere un certo numero (per esempio cinquantesette) in un numero potenzialmente infinito di modi diversi, semplicemente aggiungendo un numero arbitrario di cifre "0" a sinistra di una rappresentazione scritta dello stesso numero (ossia: 57, 057, 0057, 00057, ecc.).
D'altra parte, questa abitudine di scrivere numeri in forma minima corrisponde all'uso di un codice a lunghezza variabile, in cui numeri di valore diverso richiedono un numero di cifre diverso per la rappresentazione. Di solito questa caratteristica del codice non ci crea problemi, anche perché di solito non scriviamo numeri di valore molto grande.
Tuttavia, se vogliamo applicare l'algoritmo di addizione, uno dei requisiti é quello di poter allineare le rappresentazioni degli addendi a destra, in modo da porre sulla stessa verticale le cifre che rappresentano le unità, le decine, ecc. Se per esempio vogliamo sommare una lunga sequenza di numeri, nel momento in cui scriviamo il primo numero della lista dobbiamo assicuraci di riservare sulla sinistra uno spazio sufficiente per la scrittura di tutte le cifre del più grande degli addendi. Una volta scritto il primo addendo, la distanza dal margine sinistro del foglio della sua cifra più a destra determina implicitamente il numero massimo di cifre che potremo utilizzare per scrivere un numero allineato per una operazione di somma (almeno se ammettiamo di scrivere tutte le cifre della stessa dimensione). Questa considerazione ci mostra la necessità di stabilire un massimo valore rappresentabile quando vogliamo prefissare delle risorse da dedicare alla realizzazione di un algoritmo (per esempio una risma di fogli in formato A4).
Volendo usare un sistema di calcolo per la realizzazione di algoritmi dobbiamo preoccuparci di definire a priori delle risorse dedicate alla rappresentazione dei dati. Il modo più semplice per arrivare a gestire queste risorse nel caso della rappresentazione di numeri naturali é quello di definire a priori un valore massimo rappresentabile per ogni numero (a cui corrisponde un numero massimo di cifre impiegate per la rappresentazione), con l'accortezza di usare un valore massimo sufficientemente grande da poter trattare tutti (o quasi) i casi di rilevanza pratica, ma sufficientemente piccolo da non sprecare inutilmente risorse costose del sistema. Una volta determinato il massimo valore rappresentabile, questo determina anche il numero di cifre (decimali, binarie, ottali, o altro) da usare per la sua rappresentazione.
Un codice viene detto a lunghezza fissa quando viene sempre usato lo stesso numero di cifre per la rappresentazione di qualunque valore. Ovviamente il numero di cifre da usare é in questo caso il numero minimo di cifre per la rappresentazione del massimo valore predeterminato. Per esempio, se decidessimo di trattare numeri non superiori a 9999, potremmo usare una rappresentazione decimale posizionale fissa a 4 cifre. In tal caso il numero cinquantasette verrebbe rappresentato (in modo unico) come "0057".
Esempi pratici di uso di codici a lunghezza fissa nella vita quotidiana comprendono i numeri di telefono, ed i vari codici di sicurezza chiamati PIN associati a Bancomat, carte di credito, telefoni cellulari, ecc. Chi volesse telefonarmi da una qualunque località italiana dovrebbe comporre il numero di 10 cifre "0103536606", incurante del fatto che la prima cifra sia "0"; la composizione di un numero di cifre minore di 10 (per esempio: "103536606") non sarebbe sufficiente a stabilire la comunicazione (se fossi nel distretto di Torino con prefisso "011" stabilirebbe una comunicazione col numero di emergenza della polizia), mentre la composizione di ulteriori cifre oltre la decima (per esempio: "00103536606") comporterebbe la chiamata di un numero inesistente in Nord America.
Quando consideriamo il sistema di rappresentazione N-ario posizionale, abbiamo detto facciamo uso di un alfabeto di N simboli. Questo é vero nel caso di rappresentazioni a lunghezza fissa ma falso nel caso di rappresentazioni a lunghezza variabile. In realtà se usiamo la versione usuale della rappresentazione (senza zeri come cifra più a sinistra, quindi in rappresentazione non fissa e minimale) noi facciamo implicitamente uso di un N+1-esimo "simbolo", normalmente lo spazio bianco: l'assenza di ulteriori cifre più a sinistra (e quindi lo spazio bianco invece di una cifra) indica dove termina la rappresentazione del numero. Normalmente, infatti, interpretiamo la presenza di uno spazio bianco a sinistra di una cifra come l'indicazione che quella cifra é la cifra più significativa e che non ce ne saranno altre più a sinistra. In mancanza di questa informazione associata allo spazio vuoto, noi potremmo pensare che la cifra precedente sia scritta "un po' più a sinistra di dove abbiamo guardato sin ora", e non potremmo mai terminare la lettura di un numero. Solo il raggiungimento del margine del foglio ci darebbe la certezza che non ci sono altre cifre più a sinistra, ma se ammettiamo che esista sempre un margine a sinistra del foglio alla nostra portata visiva implicitamente poniamo un vincolo al numero massimo di cifre rappresentabili. Per risolvere questa contraddizione non ci resta che prendere atto che senza un N+1-esimo (nel nostro esempio lo spazio vuoto) non possiamo scrivere un valore in rappresentazione posizionale base N con numero arbitrario di cifre.
Da qui deriva la necessità concettuale (dal punto di vista informatico) di delimitare la cifra più a sinistra della rappresentazione nel caso di codici di rappresentazione a lunghezza variabile. In informatica si parla quindi di codici a lunghezza variabile nei casi in cui si prevede l'uso di un numero di cifre variabile in funzione del valore da rappresentare, ma tali per cui nell'alfabeto esistono dei simboli espliciti usati per individuare la terminazione della rappresentazione.
Per esempio, la normale rappresentazione decimale con numero di cifre variabile potrebbe essere facilmente trasformata in un codice ad espansione utilizzabile in un sistema di calcolo mediante la seguente modifica: usare un alfabeto ad undici simboli che includa oltre alle dieci cifre anche il carattere "#"; la cifra più a sinistra di una rappresentazione é sempre "#"; la cifra "0" non può mai seguire la cifra "#", tranne nel caso in cui sia la cifra più a destra. Usando questa regola modificata, ogni numero avrebbe ancora una rappresentazione unica. I numeri zero, uno, due, cinquantasette sarebbero rappresentati come "#0", "#1", "#2", "#57". Leggendo le cifre da destra verso sinistra, se troviamo una delle dieci cifre arabe allora sappiamo di dover continuare la lettura della rappresentazione incontrando almeno un'altra cifra verso sinistra; se invece incontriamo il simbolo di terminazione, allora sappiamo che la codifica non contiene altre cifre più a sinistra (e quindi possiamo interrompere la lettura del numero).
Un altro esempio più concreto può essere quello della codifica di una testo su un supporto informatico. Ciascun carattere (lettera alfabetica maiuscola o minuscola, cifre araba, segno di punteggiatura, spazio vuoto, ecc.) viene rappresentato come un simbolo di un alfabeto predefinito. Per esempio si può ricorrere al codice ASCII per definire un alfabeto di 128 simboli di base adatti allo scopo. In termini astratti possiamo quindi trattare una qualunque sequenza di questi caratteri come una rappresentazione in base 128. Per poter riconoscere la fine di un testo dovremo però riservare uno dei 128 simboli alla rappresentazione della informazione "fine del testo". Solo 127 caratteri ASCII resteranno quindi disponibili per la codifica del testo stesso. Normalmente nel caso di sistemi Unix e/o linguaggio di programmazione C il simbolo 0 (chiamato "nul") é riservato a questo scopo.
Nel caso dei codici a lunghezza variabile appena discusso "sprechiamo" uno dei simboli dell'alfabeto per codificare la fine delle cifre della codifica. Esistono delle alternative per ottenere un codice ad espansione a partire da un codice a lunghezza fissa senza modificare l'alfabeto. Consideriamo per esempio una rappresentazione binaria di numeri, e supponiamo di raggruppare un certo numero di cifre in "quanti" prefissati. Potremmo per esempio supporre di partire da una rappresentazione fissa su 5 cifre binarie (massimo numero rappresentabile 31), e pensare poi di aggiungere altri "gruppi di cifre" alla rappresentazione di base per rappresentare numeri superiori (non rappresentabili col numero di cifre della rappresentazione di partenza). Vediamo una serie di esempi.
Supponiamo di voler definire un codice che preveda l'uso di uno tra 4 formati di rappresentazione: uno su 4 cifre binarie, un secondo formato su 7 bit, un terzo formato su 10 bit ed un ultimo su 16 bit. I 4 formati di rappresentazione devono essere distinguibili l'uno dall'altro, quindi possiamo pensare di numerarli da 0 a 3, ed inserire il numero del formato nelle prime due cifre della rappresentazione binaria. Il primo formato sarà quindi costituito sempre dalle prime due cifre "00", seguite da altre due cifre binarie; il secondo sarà costituito sempre dalle prime due cifre "01", seguite da altre 5 cifre binarie; il terzo sarà costituito sempre da "10" seguito da altre 8 cifre binarie; l'ultimo formato sarà costituito sempre da "11" seguito da altre 14 cifre binarie. Possiamo quindi pensare di usare questo codice per rappresentare i numeri da 0 a 3 usando il primo formato su 4 cifre (0000 ÷ 0011), i numeri da 4 a 35 usando il secondo formato (0100000 ÷ 0111111), i numeri da 36 a 291 usando il terzo formato (1000000000 ÷ 1011111111) ed i numeri da 292 a 16675 usando il terzo formato (1100000000000000 ÷ 1111111111111111). Numeri piccoli verrebbero quindi rappresentati con un numero di cifre inferiore, numeri grandi con un numero di cifre superiore. Leggendo le prime due cifre a sinistra di qualsiasi rappresentazione si risale al formato usato, e quindi si capisce quante altre cifre devono essere lette prima di "arrivare alla fine" della rappresentazione stessa.
Consideriamo un caso analogo al precedente, nel quale vogliamo usare 4 possibili formati rispettivamente su 4, 7, 10 e 16 bit. Rispetto al caso precedente cambiamo la codifica del formato usato. Il formato a 4 bit viene caratterizzato da una prima cifra al valore 0, seguita da altre tre cifre binarie "utili"; il formato a 7 bit viene caratterizzato da una prima coppia di cifre al valore costante "10", seguita da altre 5 cifre binarie "utili"; il formato a 10 bit conterrà sempre le prime tre cifre "110", seguite da altre 7 cifre; il formato a 16 bit sarà costituito sempre dalle prime tre cifre "111", seguite da altre 13 cifre binarie. Possiamo quindi usare questo codice per rappresentare i numeri da 0 a 7 con il formato a 4 bit (0000 ÷ 0111), i numeri da 8 a 39 con il formato a 7 bit (1000000 ÷ 1011111), i numeri da 40 a 167 con il formato a 10 bit (1100000000 ÷ 1101111111) ed i numeri da 168 a 8359 con il formato a 16 bit (1110000000000000 ÷ 1111111111111111). Notare come, rispetto all'esempio precedente, aumenta la capacità di codificare numeri piccoli con i formati più piccoli, mentre diminuisce la capacità di rappresentare numeri grandi con i formati a numero di bit superiore.
Consideriamo nuovamente un codice ad espansione sui 4 formati di 4, 7, 10 e 16 bit, e "proviamo" un terzo modo di codificare il passaggio da un formato ad un altro. Questa volta minimizziamo lo spreco di configurazioni dedicate al riconoscimento del formato per il formato a 4 bit, riservando una sola configurazione a rappresentare l'informazione "il formato non é quello a 4 bit". Possiamo per esempio associare la sequenza di quattro cifre 1 (ossia "1111") per rappresentare l'espansione. Rimarranno quindi 15 codifiche diverse "utili" per la rappresentazione dei numeri da 0 a 14 usando il formato a 4 bit. Leggendo qualunque combinazione diversa da "1111" nelle prime quattro cifre sapremo contemporaneamente sia il valore del numero, sia che questo era stato codificato col formato a 4 bit. Leggendo invece "1111" nelle prime quattro cifre, sapremo solo che il valore é stato codificato usando uno degli altri 3 formati. In modo analogo potremo riservare una delle 8 codifiche del formato a 7 bit (per esempio "1111111") per rappresentare l'informazione "é stato usato un formato con numero di bit maggiore di 7", e lasciare quindi le rimanenti 7 codifiche su 7 bit (1111000 ÷ 1111110) per la rappresentazione dei numeri da 15 a 21. Procedendo nello stesso modo si può riservare una delle 8 codifiche a 10 bit (per esempio "1111111111") per rappresentare la condizione "é stato usato il formato a 16 bit", e sfruttare le rimanenti 7 codifiche su 10 bit per rappresentare i numeri da 22 a 28 (1111111000 ÷ 1111111110). Infine, potremo usare tutte e 64 le configurazioni del formato a 16 bit per rappresentare i numeri da 29 a 92 (1111111111000000 ÷ 1111111111111111).
Confrontato coi metodi di espansione precedentemente illustrati, questo metodo
accentua ulteriormente le caratteristiche di poter rappresentare un numero
relativamente elevato di numeri piccoli col formato contenente il numero di
cifre binarie inferiori, ma pagando questo vantaggio con l'inefficienza di
rappresentazione dei numeri più grandi su formati di dimensione
maggiore.
A seconda del tipo di applicazione potranno essere convenienti tecniche diverse
di rappresentazione dell'espansione del formato.
Ricordiamo che a questo punto stiamo considerando codici a lunghezza fissa per la rappresentazione binaria di numeri, quindi stabiliamo anzitutto un limite inferiore e superiore per i numeri rappresentabili: numeri di valore minore al limite inferiore oppure maggiore del limite superiore non saranno in ogni caso rappresentabili. Verrà quindi considerato un errore concettuale inaccettabile il tentativo di codificare un numero non appartenente all'intervallo prefissato.
Nel caso di numeri naturali (senza segno) il modo più naturale di definire i limiti di rappresentazione é quello di prendere zero come limite inferiore (in modo da includere tutti i naturali più piccoli) e 2**N-1 come limite superiore (se abbiamo scelto di usare N cifre binarie nella rappresentazione). Se passiamo al caso di numeri relativi, la scelta del limite inferiore della rappresentazione diventa meno ovvia. Un criterio che appare ragionevole consiste nel "centrare" (nel miglior modo possibile) l'intervallo dei numeri rappresentabili intorno al valore zero, in modo da poter rappresentare tutti i numeri di valore assoluto minore o uguale ad un certo valore massimo.
Questa é probabilmente la prima idea che viene in mente a chiunque per la soluzione del problema, anche tenendo conto del criterio appena enunciato circa la scelta dell'intervallo di rappresentabilità legato al valore assoluto.
La rappresentazione binaria in modulo e segno su N cifre dedica una cifra binaria (per convenzione quella più a sinistra) per codificare il segno (zero significa segno positivo, uno significa segno negativo), e le rimanenti N-1 cifre rappresentano la codifica in forma binaria fissa del valore assoluto del numero (che per definizione é un numero naturale).
A fronte dell'evidente vantaggio di semplicità di rappresentazione, questa codifica presenta due difetti molto gravi dal punto di vista della sua efficienza per la rappresentazione di numeri in un sistema di calcolo:
Anche in questo caso si utilizza la cifra binaria più a sinistra come indicatore di segno. Nel caso di segno positivo (cifra più a sinistra uguale a zero) il numero é rappresentato in forma binaria come nel caso dei numeri naturali senza segno. Nel caso di segno negativo (cifra più a sinistra uguale a uno), allora occorre negare tutte le cifre (ossia sostituire 0 con 1 e viceversa 1 con 0) per ottenere la rappresentazione binaria del modulo del numero.
Per esempio, se consideriamo rappresentazioni in complemento a 1 su 5 cifre binarie, "00110" rappresenta il numero positivo sei, mentre "10101" rappresenta un numero negativo il cui valore assoluto é dato dalla rappresentazione binaria "01010" (ottenuta negando tutte le cifre della rappresentazione del numero), quindi rappresenta il numero "meno dieci".
Notare che questa rappresentazione ha caratteristiche molto simili a quella in modulo e segno: anche in questo caso abbiamo due rappresentazioni possibili per lo zero (+0 corrisponde a "000...0", -0 corrisponde a "111...1"), ed anche in questo caso abbiamo una sostanziale corrispondenza della rappresentazione con la rappresentazione del valore assoluto (a meno della operazione di negazione, concettualmente semplice, e molto semplice anche da realizzare in un sistema di calcolo).
A differenza della rappresentazione in modulo e segno, tuttavia, questa volta ci "avviciniamo molto" alla possibilità di effettuare le operazioni di somma operando sulla rappresentazione del numero indipendentemente dal segno. Proviamo infatti ad operare su qualche esempio:
00110 + ( +6) 00101 = ( +5) 01011 (+11)Se entrambi gli addendi sono positivi, la somma funziona sulla rappresentazione a patto che il risultato sia rappresentabile (ovvero non ecceda il valore massimo prestabilito per la codifica fissa che si sta considerando, condizione di errore detta di overflow).
00110 + ( +6) 10101 = (-10) 11011 ( -4)Se gli addendi sono di segno diverso ed il risultato ha segno negativo, allora la somma delle rappresentazioni produce sempre la rappresentazione della somma (infatti in questo caso il modulo del risultato sarà sempre rappresentabile, visto che lo erano i moduli degli addendi).
11001 + ( -6) 11010 = ( -5) 10011 (-12) !!!!!!!!!!!!!!!!!!Se entrambi gli addendi hanno segno negativo oppure hanno segno diverso e generano un risultato positivo, allore le cose "funzionano quasi" correttamente nel caso in cui il risultato sia rappresentabile: infatti viene prodotta la rappresentazione del risultato corretto decrementato di uno!
Da questa ultima osservazione nasce la seguente variante di codice.
Anche in questo caso si utilizza la cifra binaria più a sinistra come indicatore di segno. Nel caso di segno positivo (cifra più a sinistra uguale a zero) il numero é rappresentato in forma binaria come nel caso dei numeri naturali senza segno. Nel caso di segno negativo (cifra più a sinistra uguale a uno), allora occorre negare tutte le cifre (ossia sostituire 0 con 1 e viceversa 1 con 0) e sommare la costante 1 per ottenere la rappresentazione binaria del modulo del numero.
Per esempio, se consideriamo rappresentazioni in complemento a 2 su 5 cifre binarie, "00110" rappresenta il numero positivo sei, mentre "10110" rappresenta un numero negativo il cui valore assoluto é dato dalla rappresentazione binaria "01001" (ottenuta negando tutte le cifre della rappresentazione del numero), sommata alla costante "00001" (ottenendo "01010"), quindi rappresenta il numero meno dieci.
Si può dimostrare matematicamente che la definizione data sopra di operazione di complemento a 2 (complemento a 1 seguito da somma della costante 1) é sempre equivalente ad un'altra sequenza di due operazioni: prima sottrarre la costante 1 e poi effettuare l'operazione di complemento a 1.
Se riproviamo gli esempi precedentemente provati per la rappresentazione in complemento a 1 nel caso di addendi di segno diverso, otteniamo:
00110 + ( +6) 10110 = (-10) 11100 ( -4)a parità di valori e cambiando la codifica del numero negativo, ovvero:
00110 + ( +6) 10101 = (-11) 11011 ( -5)a parità di codifica e cambiando il valore del numero negativo.
Se riproviamo gli esempi precedentemente provati per la rappresentazione in complemento a 1 nel caso di addendi di segno negativo, a parità di valori otteniamo:
11010 + ( -6) 11011 = ( -5) 10101 (-11)mentre a parità di codifica otteniamo:
11001 + ( -7) 11010 = ( -6) 10011 (-13)
Constatiamo quindi che la rappresentazione in complemento a 2 ci permette sempre di applicare il normale algoritmo di somma di rappresentazioni binarie senza segno per ottenere la rappresentazione del valore della somma, indipendentemente dal segno degli addendi (purché il risultato sia rappresentabile col numero di cifre binarie prefissato).
Notiamo anche che, ovviamente, la rappresentazione risultante dall'algoritmo di somma di due rappresentazioni binarie é univocamente determinata dall'algoritmo stesso, e non cambia al variare della codifica utilizzata. Il fatto che il risultato sia corretto o meno dipende quindi dalla interpretazione che diamo alla rappresentazione degli addendi e del risultato. Usando la codifica in complemento a 2 noi diamo una interpretazione tale che la decodifica del risultato corrisponde sempre esattamente al valore della somma dei valori derivanti dalla decodifica degli addendi, mentre questo accade solo in qualche caso con la codifica in complemento a 1 e in un numero ancora minore di casi con la codifica in modulo e segno.
Tra le caratteristiche della rappresentazione in complemento a 2 possiamo anche notare la rappresentazione unica del valore zero. Infatti, se applichiamo l'algoritmo di codifica per il valore -0, otteniamo (per sempio operando con 5 cifre binarie) di dover sommare la costante "00001" alla negazione della rappresentazione di zero, ossia alla rappresentazione "11111"; questa somma produce come risultato "00000" (in quanto il riporto sulla sesta cifra non può essere rappresentato e quindi viene perso), ossia la stessa rappresentazione del valore +0.
Consideriamo una rappresentazione binaria su N bit. Questo codice consiste nel riservare tutte le codifiche da 0 a (2**(N-1))-1 alla rappresentazione di numeri negativi tra -(2**(N-1)) e -1, la codifica 2**(N-1) per la rappresentazione del valore zero, e le rimanenti codifiche per la rappresentazione di numeri positivi tra 1 e (2**(N-1))-1.
L'algoritmo di costruzione della codifica a partire dal valore che si vuole codificare é semplicissimo: sommare al valore da codificare la costante 2**(N-1), ottenendo così un numero non negativo, quindi determinare la codifica binaria su N bit del numero ottenuto.
L'algoritmo di decodifica é altrettanto semplice: considerare il numero corrispondente alla rappresentazione binaria senza segno su N bit, e da questo sottrarre la costante 2**(N-1).
Si può dimostrare che la codica Eccesso 2**(N-1) su N bit é
identica alla codifica in complemento a 2 su N bit a meno dell'inversione
del bit di segno per ogni numero codificabile con i due codici.
Una volta appurato che possiamo usare il codice "complemento a 2" per interpretare una codifica binaria originariamente sviluppata per i numeri naturali anche per manipolare numeri con segno, vediamo ora se é ulteriormente possibile estendere l'interpretazione in modo da includere numeri non interi, caratterizzati da una parte frazionaria maggiore di 0 e minore di 1. Vedremo che, una volta risolto questo problema, la soluzione potrà poi essere estesa a numeri non interi con segno in modo molto semplice.
Di fatto, la rappresentazione binaria posizionale per i numeri naturali
stabilisce una corrispondenza tra la posizione delle cifre binarie
nella rappresentazione ed il loro "peso" espresso sotto forma di potenza
di 2: la cifra più a destra per convenzione assume il significato
di coefficiente di 2**0, quella immediatamente adiacente di 2**1, ecc.
Nulla ci impedisce di usare una rappresentazione binaria posizionale
associata ad una convenzione diversa, per esempio la prima cifra da
destra associata a 2**3, la seconda a 2**4, la terza a 2**5, ecc.
Se usassimo questa convenzione sapremmo rappresentare solo i numeri
multipli di 8, e per esempio scriveremmo 011 per indicare il numero
ventiquattro, invece di 011000 così come nella "normale"
rappresentazione binaria.
In modo del tutto simile possiamo associare alla cifra più a
destra il significato di una potenza
La scelta di interpretare una codifica binaria associando alla cifra più a destra il significato di una potenza negativa può essere evidenziata immaginando di "scrivere una virgola" per separare la parte intera dalla parte frazionaria. Questa "virgola immaginaria" assume una posizione fissa una volta stabilito il codice: se per esempio associamo 2**(-4) alla cifra più a destra, la nostra virgola di separazione la dovremo immaginare tra la quarta e la quinta cifra binaria partendo da destra. Siccome gli anglosassoni usano il punto per separare la parte intera dalla parte frazionaria, questo modo di codificare numeri non interi viene identificato col termine "fixed point".
Ovviamente, una volta stabilito un codice in virgola fissa su N cifre binarie, viene automaticamente definito un insieme (finito) di 2**N valori diversi codificabili. Avendo deciso di associare la potenza 2**(-M) alla cifra più a destra della rappresentazione, questi valori saranno tutti i multipli di 2**(-M) compresi tra 0 e (2**(N-M)-2**(-M)). Di conseguenza, valori non divisibili per una potenza negativa di 2 (come per esempio "un decimo") non potranno mai essere rappresentati esattamente (ma solo approssimati più o meno bene, per eccesso o per difetto) mediante una rappresentazione binaria in virgola fissa.
Per esempio, consideriamo una rappresentazione binaria su 6 bit, e "fissiamo la virgola" a metà della rappresentazione, tra la terza e la quarta cifra. La codifica "000000" (che possiamo immaginare scritta come "000.000") continua come al solito a rappresentare il numero zero. Il numero uno dovrà invece essere codificato come "001000". Il più piccolo numero maggiore di zero rappresentabile sarà un ottavo (codificato "000001"), mentre il più grande sarà sette più sette ottavi (codificato "111111"). Notare come solo l'informazione su "dove stiamo pensando di posizionare la virgola" ci permette di distinguere il valore uno nel nostro codice a virgola fissa dal valore otto che normalmente associamo alla rappresentazione binaria "001000". Per un eventuale sistema di calcolo che usasse il nostro codice per la rappresentazione di numeri, non ci sarebbe nessuna differenza tra la configurazione "001000" che rappresenta il valore 1 con la virgola fissata a metà della rappresentazione e la configurazione "001000" che noi interpretiamo come otto se invece conveniamo di usare la normale rappresentazione binaria con virgola a destra della cifra più a destra.
In modo del tutto analogo possiamo pensare di "combinare" in uno stesso codice la rappresentazione del segno in complemento a due e la rappresentazione di numeri frazionari in virgola fissa. Riprendendo l'esempio della rappresentazione su 6 bit con "virgola" tra la terza e la quarta cifra, l'introduzione del segno provoca un dimezzamento del massimo valor assoluto rappresentabile. Il minimo valore rappresentabile sarà quindi il numero negativo "meno quattro" rappresentato "100.000", mentre il massimo valore rappresentabile sarà il numero positivo tre più sette ottavi rappresentato "011.111". L'operazione di inversione di segno sarà definita dai due passi: complementazione a 1 della rappresentazione, e poi somma della costante "un ottavo" (rappresentata "000.001"). Il tutto é quindi equivalente a rappresentare un numero (naturale o relativo in complemento a 2) e moltiplicarlo poi per una costante eventualemente frazionaria (nel nostro esempio un ottavo) che tiene conto "della posizione della virgola". In generale possiamo formalizzare questo codice dicendo che il valore I che vogliamo codificare viene espresso come I = 2**E * M, dove E é una costante determinata una volta per tutte quando viene scelta la posizione della virgola, ed M é un numero intero (eventualmente con segno).
La determinazione della posizione della virgola per una rappresentazione di numeri frazionari in virgola fissa può non essere agevole in pratica. Riservando molti bit alla parte frazionaria si possono rappresentare numeri molto piccoli diversi da zero (oppure numeri non divisibili per potenze di 2 con elevato grado di approssimazione). D'altra parte se si lasciano troppo pochi bit "prima della virgola" si rischia di non riuscire a rappresentare numeri di valor assoluto più grande. In alcune applicazioni nasce quindi l'esigenza di poter "spostare la virgola" in modo da adattare il numero di bit di rappresentazione alle esigenze di rappresentazione di valori diversi. Per valori grandi si cercherà di aumentare il numero di bit a sinistra della virgola, riducendo di conseguenza il numero di bit di rappresentazione a destra della virgola, e viceversa per la rappresentazione di valori piccoli.
Questa idea tuttavia impone che la posizione della virgola entri a far parte della rappresentazione del valore codificato. Tale metodo di rappresentazione viene chiamato Floating Point, in quanto permette di adattare la posizione della virgola alle esigenze del particolare valore che stiamo considerando. Il punto di partenza é nuovamente la formula: I = 2**E * M, dove I rappresenta il valore che vogliamo rappresentare, E ed M sono valori che soddisfano l'equazione e che possono essere codificati in modo efficiente in Fixed Point. Verrà quindi usata una rappresentazione binaria opportuna della coppia di valori E ed M in sostituzione della rappresentazione diretta del valore I.
Supponiamo di restringere E ad assumere solo valori interi positivi o negativi.
Potremmo quindi pensare di usare un codice complemento a due oppure eccesso
2**(K-1) per rappresentarne il valore su K bit (K sarà una costante
predefinita).
Queste restrizioni non sono tuttavia sufficienti per ottenere una decomposizione
unica di valori I in coppie di valori E ed M.
Per esempio, pensando di valor rappresentare il valore I = (cinque e mezzo),
possiamo individuare un insieme infinito di coppie di valori (E,M) che soddisfano
l'equazione, per esempio (in notazione decimale) ... (-2,22), (-1,11), (0,5.5),
(1,2.75), (2,1.375), (3,0.6875), (4,0.34375), ...
Al fine di arrivare ad una rappresentazione
La condizione di normalizzazione ci permette di definire una rappresentazione
in Fixed Point molto efficiente per la mantissa M.
Infatti la rappresentazione binaria di M assumerà
L'eventuale segno del numero viene normalmente codificato a parte con un singolo bit (come nel caso della rappresentazione in Modulo e Segno per gli interi). Si arriva pertanto a comporre una rappresentazione su 1+K+L bit per un numero in Floating Point, di cui 1 bit per rappresentare il segno del numero, K bit per rappresentare l'esponente E ed L bit per rappresentare la mantissa M del modulo del numero. Per esempio, fissando K=3 ed L=6, si potrebbe definire una rappresentazione floating point normalizzata nella quale il numero "cinque e mezzo" sarebbe rappresentato come "0011011000", ovvero, da sinistra a destra, "0" per il segno positivo, E="011", M-½ = "0.011000" * ½.
Oggigiorno non sono più i singoli progettisti o produttori di sistemi a stabilire il codice da usare per la rappresentazione Floating Point dei numeri all'interno di un sistema di calcolo. La soluzione di questo problema ha ormai raggiunto un livello di maturità tale da consentire ad organismi internazionali di definire degli Standard a cui tutti i progettisti e costruttori si devono adeguare.
In particolare, lo standard più diffuso é quello stabilito dall'IEEE (Institute for Electrical and Electronics Engineering) e identificato dalla sigla 754. Questo prevede due formati di rappresentazione, uno in "precisione normale" codificato su 32 bit, ed uno in "doppia precisione" codificato su 64 bit. Entrambi usano la tecnica della rappresentazione normalizzata della mantissa vista in precedenza. Oltre ai numeri in forma normalizzata, lo standard IEEE prevede anche una serie di codici per rappresentare "situazioni anomale" derivanti dalla applicazione di operazioni algebriche su alcuni numeri, quali la divisione per zero. I due formati adottano la stessa tecnica e le stesse convenzioni di rappresentazione, e differiscono solo per il numero di bit di rappresentazione di E ed M:
I valori di E sono codificati in codice Eccesso 127 (NON Eccesso 128!), e possono rappresentare solo i numeri nell'intervallo tra -126 e +127 (ossia i codici tra 01 e 3e in esadecimale).
Il valore 00 (esadecimale) per il campo E viene usato per indicare
una rappresentazione
Il valore ff (esadecimale) per il campo E viene usato per indicare il risultato di una divisione per zero: "Infinito" (rappresentato con M=0) nel caso in cui si divida per zero un numero diverso da zero; "NaN" (Not a Number) nel caso in cui si divida zero per zero (rappresentato con M>0).
I valori di E sono codificati in codice Eccesso 1023 (NON Eccesso 1024!), e possono rappresentare solo i numeri nell'intervallo tra -1022 e +1023 (ossia i codici tra 001 e 7fe in esadecimale).
Il valore 000 (esadecimale) per il campo E viene usato per indicare
una rappresentazione
Il valore 7ff (esadecimale) per il campo E viene usato per indicare il risultato di una divisione per zero: "Infinito" (rappresentato con M=0) nel caso in cui si divida per zero un numero diverso da zero; "NaN" (Not a Number) nel caso in cui si divida zero per zero (rappresentato con M>0).
Abbandoniamo ora il problema di rappresentazione di numeri in forma binaria, e generalizziamo l'approccio al caso di codifica sotto forma binaria di informazioni arbitrarie.
Ovviamente se consideriamo un insieme finito di valori possibili che le nostre informazioni possono assumere, possiamo sempre ricondurci ad elencare in una lista di dimensione finita tutti i possibili valori che la nostra informazione può assumere, e poi usare il numero d'ordine del valore considerato all'interno della nostra lista per codificare l'informazione sotto forma numerica. Quindi possiamo poi usare la rappresentazione binaria dei numeri naturali per codificare in forma binaria tale numero d'ordine, e con questo il gioco é fatto.
Perché quindi dobbiamo preoccuparci della codifica di informazioni non numeriche (se da qualunque informazione possiamo ottenere una rappresentazione numerica)? Il motivo deriva dal fatto che sulla codifica di informazioni non numeriche normalmente non saremo interessati ad operare manipolazioni aritmetiche. Quindi, per esempio, la codifica in complemento a due non porterebbe in questo caso nessun vantaggio rispetto alle altre codifiche numeriche esaminate. Le uniche operazioni che saremo interessati a realizzare in modo efficiente saranno in questo caso i confronti per determinare l'uguaglianza o la diversità tra due o più codifiche dello stesso tipo.
Una volta eliminato il vincolo di dover supportare operazioni aritmetiche, possiamo pensare di poter trovare dei codici di rappresentazione più efficienti della normale rappresentazione binaria fissa per informazioni di tipo non numerico. Normalmente ci interessa ridurre il più possibile il numero di cifre binarie utilizzate per codificare un certo tipo di informazione. L'unico vincolo che dobbiamo garantire é quello di unicità della rappresentazione per ogni valore possibile dell'informazione. Se questo vincolo é soddisfatto, possiamo infatti realizzare il confronto direttamente sulle codifiche dell'informazione.
Per formalizzare il problema introduciamo il concetto di ridondanza di un codice come il rapporto tra il numero di configurazioni possibili di una codifica (2**N se consideriamo una codifica fissa su N cifre binarie) ed il numero di valori possibili che l'infomazione che vogliamo trattare può assumere. Ovviamente questo rapporto non potrà mai scendere sotto il valore 1, altrimenti sarebbe impossibile codificare tutti i valori della informazione da trattare. Diremo che il codice binario di rappresentazione é minimale se questo rapporto é minore di 2: infatti se eliminassimo anche una sola cifra binaria dalla rappresentazione fissa otterremmo un codice nel quale il numero di configurazioni possibili é strettamente inferiore al numero di valori che l'informazione può assumere, quindi non utilizzabile.
Consideriamo un esempio in cui vogliamo codificare le 21 lettere dell'alfabeto italiano. Un codice binario fisso minimale sarà composto da 5 cifre binarie, ed avrà una ridondanza di 32/21. La corrispondenza tra codifica e valore può essere ottenuta elencando le lettere in ordine alfabetico, ed associando quindi la codifica "00000" alla lettera "A", "00001" alla lettera "B", ... "10100" alla lettera "Z"; le codifiche da "10101" a "11111" rimarrebbero invece inutilizzate (potremmo facilmente trovare una utilizzazione per le 10 cifre arabe e per il carattere "spazio vuoto" in modo da arricchire l'insieme delle informazioni codificabili, ma questo é un altro discorso).
Consideriamo nuovamente l'esempio in cui vogliamo codificare le 21 lettere dell'alfabeto italiano. Supponiamo però questa volta di poter identificare delle lettere che vengono usate più frequentemente di altre, come per esempio le 5 vocali contrapposte alle 16 consonanti.
Per poter codificare le 5 vocali da sole, occorrerebbe utilizzare una codifica binaria fissa su 3 cifre, mediante la quale, d'altra parte, riusciamo a individuare 8 valori diversi. Potremmo pensare di usare le prime 5 codifiche (da "000" a "100") per rappresentera le 5 vocali (ordinate alfabeticamente), e le rimanenti 3 codifiche ("101", "110" e "111") per espandere il codice designando quindi l'utilizzazione di un codice diverso, con numero di cifre superiore a 3, per la rappresentazione delle altre lettere.
Sempre a titolo di esempio potremmo pensare di poter suddividere le 16 consonanti in due sottoinsiemi di 8 lettere ciascuno, in base alla frequenza di utilizzazione nella scrittura di parole. Immaginiamo di poter affermare sulla base di una statistica derivata dall'analisi di un testo di grandi dimensioni, che le 8 consonanti "B", "C", "F", "L", "M", "N", "R", e "S" vengano usate più frequentemente delle altre 8. Sulla base di questa informazione, potremmo dividere l'insieme delle 8 consonanti più utilizzate in due sottoinsiemi da quattro lettere, tra le quali potremo distinguere mediante una codifica binaria su 2 cifre. Le rimanenti 8 consonanti meno utilizzate, potrebbero essere elencate a parte in ordine alfabetico, e saremo quindi in grado di riconoscerne una nel sottoinsieme attraverso una codifica binaria su 3 cifre.
Riassumendo, potremo costruire 3 diverse espansioni di codice, due utilizzando rappresentazioni su 5 cifre totali (caratterizzate dai prefissi "101**" e "110**") per la rappresentazione delle 8 consonanti più frequenti, ed una su 6 cifre totali (caratterizzata dal prefisso "111***") per la rappresentazione delle 8 consonanti meno frequenti.
Con questa tecnica di codifica ad espansione, la lettera "C" verrebbe rappresentata dalla codifica "10101", la lettera "N" verrebbe rappresentata dalla codifica "11001" e la lettera "H" verrebbe rappresentata dalla codifica "111010". Rispetto alla codifica binaria fissa minimale, otteniamo un codice che usa meno cifre per le vocali (3 anziché 5), lo stesso numero di cifre per le 8 consonanti usate con più frequenza nella scrittura dei testi, ed un numero di cifre superiore (6 anziché 5) per le consonanti di uso meno frequente.
Se usiamo il nostro codice ad espansione per la memorizzazione di un testo, otteniamo quindi una rappresentazione complessiva del testo più compatta. Esempio: la frase "La mia cara mamma cucina molto bene" (composta da 29 caratteri, ignorando gli spazi) richiede 145 cifre binarie (ovvero 29*5) per la rappresentazione nella codifica fissa minimale delle lettere (esclusi gli spazi), mentre richiede solo 118 cifre binarie usando il codice ad espansione appena illustrato (14*3 + 14*5 + 1*6). Questo esempio dimostra il principio di funzionamento degli algoritmi di compressione delle informazioni usati per ridurre la quantità di memoria occupata per la memorizzazione di informazioni in un sistema di calcolo.
Oltre a questo utilizzo nella compressione della rappresentazione dei dati, i codici ad espansione vengono anche comunemente impiegati per la definizione della codifica in celle di memoria delle istruzioni di una macchina convenzionale. In tal caso l'obiettivo principale é normalmente di riuscire a confinare all'interno di una singola cella di memoria sia il codice identificativo dell'istruzione, sia la codifica dei suoi eventuali operandi. Per raggiungere tale scopo, le istruzioni vengono suddivise in sottoinsiemi secondo il numero e la lunghezza delle rappresentazioni degli operandi, assegnando quindi un numero inferiore di cifre per la rappresentazione dell'istruzione a quelle istruzioni che devono usare un numero superiore di cifre per la rappresentazione degli operandi. Vedremo successivamente, parlando di insiemi di istruzioni di macchine convenzionali, esempi di applicazione di questa tecnica.
Viene normalmente definita per codici binari a lunghezza fissa. Date due codifiche C1 e C2 dello stesso codice, la distanza di Hamming H(C1,C2) é data dal numero di cifre binarie differenti a parità di posizione. Distanza di Hamming H(C1,C2)=0 significa che C1 e C2 non differiscono in alcuna cifra, quindi le due codifiche sono uguali. Il massimo valore che la distanza di Hamming può assumere é ovviamente uguale al numero di cifre della rappresentazione, quindi é una costante predeterminata per ogni codice fisso.
Dato un qualsiasi codice fisso minimale per la rappresentazione di informazioni su N cifre binarie, possiamo sempre individuare due codifiche diverse C1 e C2 appartenenti al codice (ossia associate a due valori diversi da codificare) avente distanza di Hamming uguale ad 1. Solo un codice non minimale permette di avere distanza di Hamming maggiore o uguale a 2 tra qualsiasi coppia di codifiche valide. Tale affermazione può essere dimostrata come un Teorema; provate a pensare uno schema di dimostrazione e poi confrontatelo con lo schema di dimostrazione proposto qui.
Codici ridondanti nei quali la distanza di Hamming tra due qualsiasi codifiche valide C1 e C2 sia maggiore di 1 permettono di rilevare la presenza di errori. Consideriamo per esempio il caso di una trasmissione di informazioni codificate in forma binaria a distanza, magari mediante una linea telefonica. Tipicamente le informazioni verranno trasmesse da un luogo all'altro un bit alla volta, e occasionalmente uno o più di questi bit potranno per errore essere invertiti (determinando, per esempio la ricezione di 1 a fronte dell'invio di 0, o viceversa). La distanza di Hamming tra la codifica C1 trasmessa e la codifica C2 ricevuta dall'altro corrispondente misura il numero di errori commessi durante la trasmissione. Ovviamente un ipotetico osservatore esterno potrebbe facilmente accorgersi di questi errori confrontando i bit ricevuti con quelli inviati. Il problema che ci poniamo, invece, é quello di mettersi nei panni del ricevitore (che non conosce, ovviamente, la codifica C1) e, sulla base della sola codifica ricevuta C2 cercare di capire se si sono manifestati errori di trasmissione oppure no.
Tale problema é risolubile solo se il coefficiente di ridondanza del codice é strettamente maggiore di uno. Per esempio, se usassimo un codice minimale a 4 bit per la rappresentazione delle cifre decimali da 0 a 9 (detto comunemente codice BCD, da Binary Coded Decimal), ricevendo la codifica "0011" (corrispondente al valore 3) non ci sarebbe modo di sapere se il dato ricevuto é corretto o meno: potrebbe essere stato per esempio determinato da un errore sull'ultima cifra binaria (ossia derivare dalla codifica "0010" a distanza di Hamming uno), oppure da due errori sulla prima e la terza cifra (ossia derivare dalla codifica "1001" a distanza di Hamming due), oppure dalla corretta trasmissione del valore tre. D'altra parte, se riceviamo "1011" (corrispondente al valore 11) allora sappiamo per certo che si é verificato almeno un errore, perchè la codifica ricevuta non fa parte di quelle usate per la rappresentazione di cifre decimali in codice BCD. Quindi possiamo riconoscere la presenza di errori solo se alcune tra le combinazioni di valori delle cifre binarie non vengono mai usate in trasmissione e noi riceviamo proprio una di quelle combinazioni che sappiamo non possono essere state prodotte dal mittente.
Formalizziamo meglio l'idea che possiamo dedurre da questo esempio. Consideriamo un codice binario fisso su N bit. L'insieme delle 2**N combinazioni diverse di cifre binarie viene suddiviso in due sottoinsiemi disgiunti U e V, che raggruppano rispettivamente tutte le codifiche usate (dal trasmettitore e riconosciute come "corrette" dal ricevitore) e tutte le codifiche vietate (ossia quelle che verranno interpretate come segnalazione di errore in ricezione e mai usate dal trasmettitore). Supponiamo quindi di partire da una codifica c1 usata (ossia c1 appartenente all'insieme U) e di introdurre k>0 errori nella sua rappresentazione, in modo da ottenere una diversa codifica c2. Per definizione avremo H(c1,c2)=k. Inoltre vorremmo che fosse verificata la condizione: "c2 appartiene all'insieme V", in modo da poter rilevare la presenza di questi k errori. Non é difficile arrivare a concludere che una condizione sufficiente affinchè sia verificata la condizione di rilevazione di k errori é che l'insieme U sia costituito da elementi tali per cui per ogni coppia Ca, Cb di elementi di U valga la condizione H(Ca,Cb)>k. Quindi, in particolare, se vogliamo definire un codice ridondante in grado di riconoscere la presenza di un errore, sarà sufficente che tutte le coppie di codifiche usate soddisfino la condizione H(Ca,Cb)>1.
Cominciamo col trovare un metodo sistematico per definire un codice ridondante che goda della proprietà: per ogni coppia di codifiche valide C1 e C2, la distanza di Hamming H(C1,C2)>1.
Possiamo partire da un codice minimale per il quale la proprietà non é soddisfatta, ed aggiungere una cifra binaria più a sinistra. Tale cifra binaria aggiuntiva verrà chiamata bit di parità, ed il valore da assegnare a questa cifra viene calcolato come segue: se la codifica originaria C1 nel codice minimale contiene un numero pari di cifre 1, allora la cifra aggiuntiva deve assumere il valore 0, altrimenti (cioé se C1 contiene un numero dispari di cifre al valore 1), allora la cifra aggiuntiva deve assumere il valore 1. La codifica ridondante C1' ottenuta applicando tale algoritmo alla codifica minimale C1, sarà caratterizzata dall'avere sempre un numero pari di cifre al valore 1 per ogni codifica valida. Nessuna codifica con numero dispari di cifre al valore 1 può mai essere prodotta da tale algoritmo.
É facile dimostrare che una codifica ridondante con un bit di parità gode della proprietà richiesta. Prendiamo due codifiche C1 e C2 del codice minimale originario, tali che H(C1,C2)=1. Tali codifiche differiranno per una e una sola cifra binaria, per definizione. Supponiamo di identificare tale cifra differente e, senza nessuna perdita di generalità del ragionamento, supponiamo che questa cifra assuma il valore 0 in C1 e 1 in C2. Calcoliamo poi il bit di parità per C1 e per C2. I due bit di parità assumeranno sicuramente valori diversi, in quanto se il numero di cifre a 1 in C1 é pari, allora deve essere dispari per C2, e viceversa. Quindi le due codifiche estese col bit di parità differiranno per due cifre (quella originale e quella di parità), determinando quindi un valore di distanza H(C1',C2')=2. Notiamo infine che l'aggiunta di cifre alle configurazioni non può ridurre la distanza di Hamming ma può solo aumentarla. Con questo abbiamo quindi dimostrato la nostra proprietà fondamentale per i codici minimali con l'aggiunta di un bit di parità
Passiamo adesso alla discussione di come possiamo far uso della proprietà sulla distanza di Hamming di un codice minimale con l'aggiunta di un bit di parità per la rilevazione di errori. Anzitutto dobbiamo definire cosa intendiamo per errore. Tipicamente all'interno di un sistema di calcolo ci si preoccupa della possibilità di occorrenza di errori in due situazioni particolari: lo scambio di informazioni tra due o più sistemi fisicamente distinti, oppure la memorizzazione di informazioni su dispositivi ad altissima densità di integrazione. Nel primo caso si fa uso di tecniche di trasmissione di informazioni basati su linee di comunicazione mediante l'uso di fenomeni elettromagnetici; tali linee sono sovente soggette a disturbi elettromagnetici esterni, che possono introdurre degli errori del tipo: una o più cifre binarie usate per la codifica di informazioni cambiano valore alla ricezione rispetto al valore trasmesso. Nel secondo caso, per ridurre la potenza elettrica dissipata dal dispositivo di memoria e renderne quindi possibile il funzionamento a temperatura ambiente, si tende a ridurre la differenza di energia tra la codifica delle cifre binarie 0 ed 1; anche in questo caso una perturbazione elettromagnetica esterna può determinare una commutazione della cifra memorizzata da 0 a 1 o viceversa. Normalmente si assume che la probabilità di occorrenza di molti errori simultaneamente sia molto bassa rispetto alla probabilità di occorrenza di pochi errori.
L'uso di un codice con un bit di parità permette di riconoscere sempre la presenza di un numero dispari di errori (un solo errore, tre errori, cinque errori, ecc.). Questo riconoscimento può essere realizzato dal sistema ricevitore (oppure in fase di lettura di un valore precedentemente memorizzato) semplicemente contando il numero di cifre al valore 1 presenti nella codifica ricevuta (o letta dal dispositivo di memoria). Il valore sarà dispari se e solo se la codifica é stata soggetta ad un numero dispari di errori sulle cifre binarie della sua codifica. Se invece il controllo di parità rileva un numero pari di cifre al valore 1, allora la codifica avrà subito un numero pari di errori (nessun errore, oppure 2 errori, 4 errori, 6 errori, ecc.). Purtroppo il controllo di parità non é in grado di differenziare il caso "nessun errore" dagli altri casi di numero pari di errori. Per questo si può solo far affidamento sulla probabilità via via inferiore di occorrenza di un numero pari di errori maggiore o uguale a 2 (rispetto al caso di numero dispari di errori maggiore o uguale a 1).
Errori simultanei in numero multiplo di due possono essere riconosciuti usando dei codici (detti di Hamming) più sofisticati in grado di effettuare anche alcuni tipi di correzione di errori . Prima di passare agli aspetti di correzione di errori, esaminiamo tuttavia il problema di riconoscere l'occorrenza di 2 errori simultanei. Cominciamo ad esaminare il caso semplice di informazione codificata originariamente su una sola cifra binaria, poi estenderemo la tecnica per trattare codici ottimali con più cifre binarie.
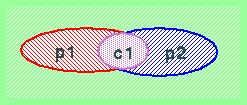
Un modo apparentemente ovvio per arrivare a riconoscere la presenza di due errori simultanei in un codice per la rappresentazione di informazioni su un solo bit (non lasciatevi ingannare dal giochetto, in quanto l'informazione originaria é rappresentata su un solo bit, e quindi non può essere soggetta a più di un errore, ma il codice ridondante col controllo di parità prevede l'uso di un numero di bit superiore, e quindi la codifica ridondante può essere soggetta ad errori multipli, fino ad un massimo pari al numero di cifre della codifica ridondante) consiste nell'usare due bit distinti di parità. Il principio di funzionamento di questo codice é illustrato dalla seguente figura che illustra sotto forma di diagrammi di Venn l'intersezione tra due insiemi:

In questa schematizzazione sono rappresentati i due bit di parità "p1" e "p2" ed il bit di codifica iniziale "c1". I due insiemi rappresentano gli insiemi di bit per i quali deve valere la condizione di parità: l'insieme rosso rappresenta i bit coperti dal bit di parità "p1" (in questo caso il bit "p1" stesso ed il bit di informazione "c1"); l'insieme blu rappresenta i bit coperti dal bit di parità "p2" (in questo caso il bit "p2" stesso ed il bit di informazione "c1"). Le codifiche ammesse saranno solo "000" e "111"; tutte le altre 6 codifiche violano almeno una delle condizioni di parità rappresentate dai due insiemi. Si vede quindi come la Distanza di Hamming tra le due codifiche consentite sia 3. Qualunque combinazione di un errore singolo oppure due errori simultanei non può quindi condurre ad una codifica valida a partire da una codifica valida. Abbiamo così dimostrato che questo codice é in grado di rilevare sempre la presenza di uno o due errori (mentre non può rilevare la presenza di 3 errori simultanei).
Lo stesso schema di principio può essere adottato per derivare codici di Hamming in grado di rilevare la presenza di uno o due errori nel caso di informazioni rappresentate su più cifre binarie, ma l'estensione non é banale. Supponiamo infatti di provare ad aggiungere semplicemente un secondo bit di dati "c2" allo schema illustrato in figura, anch'esso coperto dalla stessa coppia di bit di parità "p1" e "p2". Consideriamo poi una qualsiasi coppia di codifiche Ca e Cb che differiscano per l'inversione di entrambi i valori dei bit di dato c1 e c2. Ovviamente entrambi i bit di parità (essendo calcolati rispetto allo stesso insieme di bit di dati) produrranno lo stesso valore, e questo valore sarà identico per le codifiche Ca e Cb (in quanto l'inversione di due bit mantiene la stessa condizione di parità). Per esempio potremmo considerare Ca=1101 e Cb=1011 (che differiscono sui due bit di dato, ma coincidono sui due bit di parità). Entrambe le codifiche verrebbero classificate come appartnenti all'insieme U (in quanto verificano le due condizioni di parità), pur avendo distanza di Hamming H(Ca,Cb)=2. Tale codice non potrebbe quindi rilevare con certezza tutte le occorrenze di due errori.
Per arrivare a definire un codice dotato della proprietà di garantire distanza di Hamming maggiore o uguale a 3 per qualunque coppia di elementi dell'insieme U, dobbiamo quindi fare in modo che i controlli di parità operino su insiemi diversi tra loro per almeno un bit, in modo da evitare che la presenza di due errori simultanei in un insieme possa essere ignorata da tutti i bit di parità. Consideriamo il diagramma di Venn che rappresenta l'intersezione fra tre insiemi di base (ciascuno associato ad un diverso controllo di parità):
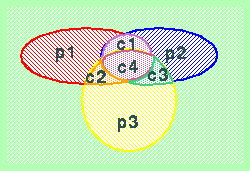
Le aree distinte di intersezione sono quattro, e ciascuna di queste può essere associata ad un diverso bit di codifica delle informazioni (indicate con "c1", "c2", "c3" e "c4"). L'insieme rosso rappresenta il controllo di parità associato al bit di parità "p1", e copre, oltre al bit di parità stesso, anche i 3 bit di informazione "c1", "c2" e "c4". Il bit di informazione "c4" risulta essere quindi coperto da tutti e tre i bit di parità "p1", "p2" e "p3". Gli altri tre bit di informazione sono coperti ciascuno da due bit di parità ("c1" da "p1" e "p2", "c2" da "p1" e "p3", "c3" da "p2" e "p3").
Anche in questo caso si può constatare (provando tutte le possibilità) che una qualsiasi disposizione di errori singoli oppure coppie di errori simultanei conduce al fallimento di almeno uno dei tre controlli di parità. Anche in questo caso si può dimostrare che la minima distanza di Hamming tra qualsiasi coppia di codifiche ammesse (ossia che soddisfano tutte e tre le condizioni di parità) vale 3.
Provate a rappresentare mediante un diagramma di Venn tutte le intersezioni possibili tra 4 insiemi. Potrete così convincervi che mediante l'uso di un codice con 4 bit di parità é possibile coprire 11 bit di informazione in modo che ciascuno di questi sia coperto da almeno due distinti bit di parità. Usando 4 bit di parità é dunque possibile trasformare un codice fisso minimale su 11 bit in un codice Hamming su 15 bit con distanza di Hamming maggiore o uguale a 3 tra ogni coppia di codifiche valide, capace quindi di rilevare la presenza di uno o due errori simultanei.
In generale, si può costruire un codice Hamming a rilevazione di 2 errori con P bit di parità in grado di coprire 2**P-P-1 bit di informazione. L'efficienza del codice, espressa come rapporto tra il numero di bit di informazione ed il numero totale di bit del codice Hamming cresce e tende asintoticamente a 1 al crescere del numero di bit, quindi da un punto di vista pratico risulta conveniente applicare questa tecnica di codifica ad insiemi composti da molti bit di informazione. Tuttavia non si può esagerare nell'aumento del numero di bit di codifica, in quanto fatalmente aumenta anche la probabilità di errore con l'aumentare del numero di bit utilizzati.
Il metodo di definizione di codici Hamming può essere anche esteso per riconoscere la presenza di più di due errori. In generale, per riconoscere la presenza di E errori é necessario utilizzare un codice nel quale la distanza di Hamming tra due qualsiasi codifiche valide sia maggiore di E. Per esempio, volendo rilevare la presenza di uno, due o tre errori simultanei, occorre una distanza di Hamming maggiore di 3 tra ogni coppia di codifiche valide, cosa che può essere ottenuta coprendo ogni bit di informazione con almeno tre controlli di parità diversi. Per esempio, utilizzando 4 bit di parità si possono arrivare a coprire 5 bit di informazione dalla occorrenza di tre errori, secondo il seguente schema di copertura: "c5" da tutti e quattro i bit di parità; "c1" da "p1", "p2" e "p3" "c2" da "p1", "p3" e "p4" "c3" da "p1", "p2" e "p4" "c4" da "p2", "p3" e "p4". In generale con P>2 bit di parità saremo in grado di coprire 2**P-P*(P-1)/2-P-1 bit di dati dall'occorrenza di un numero di errori fino a 3.
L'idea di correzione degli errori, a differenza della rilevazione usando codici Hamming, é strettamente basata sul concetto di probabilità decrescente per errori simultanei multipli. In particolare, per poter correggere un errore si ipotizza che la probabilità di un solo errore sia molto maggiore della probabilità di due errori simultanei (oppure si esclude del tutto la possibilità di due errori simultanei).
Partendo da questo presupposto, se utilizziamo un codice Hamming con distanza minima dispari (per esempio 3, come nel caso del codice Hamming per la rilevazione di due errori) allora possiamo utilizzare la distanza di Hamming per misurare la distanza tra una codifica errata e le codifiche ammissibili, identificando tra le codifica ammissibili quella a distanza minima. Tale codifica ammissibile verrà adottata come "correzione" dell'errore rilevato. Il fatto che la distanza minima tra qualunque coppia di codifiche ammissibili sia dispari garantisce l'esistenza e l'unicità di una codifica ammissibile a distanza minima da una qualsiasi codifica erronea.
Consideriamo il seguente codice Hamming a 7 bit (con 3 bit di parità e 4 bit di informazione): (c4,c3,c2,p3,c1,p2,p1) Notare che, numerando le cifre binarie da destra verso sinistra e partendo da uno, i bit di parità sono stati inseriti in corrispondenza delle posizioni potenze di due (1, 2 e 4 in questo caso). Il bit di parità "p1" copre i bit di posizione 1, 3, 5 e 7; il bit di parità "p2" copre i bit di posizione 2, 3, 6 e 7; il bit di parità "p3" copre i bit di posizione 4, 5, 6 e 7. Data una qualsiasi codifica possiamo verificare l'assenza di uno o due errori verificando che il controllo di parità sia soddisfatto per tutti e tre i sottoinsiemi di bit.
Se il test fallisce, allora sappiamo che si é verificato almeno un errore.
Nell'ipotesi che si sia verificato un
Esempio: "1101000" é una codifica erronea in quanto falliscono
i controlli di parità sul primo e sul terzo insieme.
Ipotizzando la presenza di un solo errore, questo risulta essere quindi
individuato sulla cifra di posizione "101" (ossia la quinta cifra partendo
da destra).
La correzione di questo errore porta a scrivere la codifica "1111000",
la quale soddisfa tutti i controlli di parità ed ha distanza di Hamming
minima (uguale ad 1) dalla codifica erronea.
Ipotizzando invece l'occorrenza di 2 errori si arriverebbe alla codifica
"1100001" la quale soddisfa tutti i controlli di parità
ed ha distanza di Hamming 2 dalla codifica erronea data.
Riportiamo qui brevemente alcuni altri tipi di codici usati comunemente per la rappresentazione di diversi tipi di informazioni all'interno di un sistema di calcolo. Scopo di questo riassunto é quello di avere sotto mano la definizione dei codici in modo da poter eventualmente portare a termine degli esercizi basati sul loro uso.
É un codice fisso definito su 7 bit. Rappresenta lo standard di fatto per la rappresentazione di caratteri stampabili all'interno di un sistema di calcolo. Riportiamo sotto forma di tabellina la corrispondenza tra codifiche (espresse in codice esadecimale per sinteticità) e caratteri stampati:
00 nul 01 soh 02 stx 03 etx 04 eot 05 enq 06 ack 07 bel
08 bs 09 ht 0A nl 0B vt 0C np 0D cr 0E so 0F si
10 dle 11 dc1 12 dc2 13 dc3 14 dc4 15 nak 16 syn 17 etb
18 can 19 em 1A sub 1B esc 1C fs 1D gs 1E rs 1F us
20 sp 21 ! 22 " 23 # 24 $ 25 % 26 & 27 '
28 ( 29 ) 2A * 2B + 2C , 2D - 2E . 2F /
30 0 31 1 32 2 33 3 34 4 35 5 36 6 37 7
38 8 39 9 3A : 3B ; 3C < 3D = 3E > 3F ?
40 @ 41 A 42 B 43 C 44 D 45 E 46 F 47 G
48 H 49 I 4A J 4B K 4C L 4D M 4E N 4F O
50 P 51 Q 52 R 53 S 54 T 55 U 56 V 57 W
58 X 59 Y 5A Z 5B [ 5C \ 5D ] 5E ^ 5F _
60 ` 61 a 62 b 63 c 64 d 65 e 66 f 67 g
68 h 69 i 6A j 6B k 6C l 6D m 6E n 6F o
70 p 71 q 72 r 73 s 74 t 75 u 76 v 77 w
78 x 79 y 7A z 7B { 7C | 7D } 7E ~ 7F del
Una delle caratteristiche più rilevanti di questo codice é quella di
mantenere gli ordinamenti delle rappresentazioni delle cifre numeriche e
l'ordinamento alfabetico delle lettere, sia nella versione maiuscola che
minuscola.
Questa caratteristica consente di effettuare delle operazioni di confronto
lessicografico e di verifica di appartenenza ad intervalli senza decodificare
i dati.
Per quanto riguarda il massimo valore positivo rappresentabile, questo corrisponde al caso in cui tutte le cifre tranne quella di segno assumono il valore 1, ovvero 1+2+4+8+16=31.
Per il minimo numero negativo, questo corrisponde al caso in cui la cifra del segno assume il valore 1, e tutte le altre cifre il valore 0 (in quanto il valore assoluto viene calcolato negando le cifre della rappresentazione, ed ottenendo in tal modo tutti 1). In tal caso, il valore assoluto del numero negativo più piccolo viene calcolato sommando la costante uno alla rappresentazione binaria "011111", ossia come valore della rappresentazione binaria su 6 cifre "100000" uguale a 32. Quindi il minimo numero rappresentabile é -32.
Notare la leggera asimmetria dei limiti rispetto al valore zero.
Questo deriva dal fatto che abbiamo ridotto con questa codifica il numero
di rappresentazioni associate al valore zero.
Ricordiamo che nella codifica in complemento a 1 la sequenza di cifre
"100000" era la rappresentazione di -0, ed ora (nella codifica in
complemento a 2) tale codifica viene "riciclata" per la rappresentazione
di un ulteriore numero negativo.
Lemma: Consideriamo un qualsiasi numero pari M; indichiamo con C1 la sua codifica binaria; la cifra più a destra di C1 sarà ovviamente uguale a zero. Consideriamo ora il numero dispari M+1, ed indichiamo con C2 la sua rappresentazione binaria; la cifra più a destra di C2 sarà necessariamente uguale ad uno, mentre le rimanenti cifre saranno uguali alle corrispondenti cifre di C1. Quindi la distanza di Hamming tra C1 e C2 sarà H(C1,C2)=1.
Sulla base di tale Lemma, possiamo dimostrare il nostro teorema semplicemente
dimostrando che per un codice minimale non riusciamo mai a codificare tutte
le informazioni evitando di usare un numero pari ed il suo successore,
mentre questo lo possiamo fare usando un codice binario non minimale.
Tale dimostrazione può essere facilmente ottenuta considerando
che il rapporto di ridondanza per un codice minimale é minore di 2.
Questo fa si che non si possano codificare tutte le informazioni usando
solo il sottoinsieme delle codifiche pari oppure solo il sottoinsieme delle
codifiche dispari (perché entrambe in numero inferiore rispetto
al numero di valori diversi da codificare).
Se usiamo anche un solo numero dispari oltre a tutti i pari, allora questo
sarà necessariamente il successore di uno dei numeri pari;
viceversa, se usiamo anche un solo numero pari oltre a tutti i dispari,
allora questo sarà necessariamente il predecessore di uno dei dispari
utilizzati.
Questo ragionamento può essere applicato anche a qualunque sottoinsieme
di codifiche e di valori da codificare, permettendoci così di dimostrare
il teorema anche nel caso in cui si consideri un qualsiasi numero minore del
massimo per la scelta di codifiche pari o dispari.