METODO DELLE CORDE

Il metodo delle corde è un metodo iterativo più efficiente per calcolare le radici di un’equazione non lineare ¦(x) reale e continua in un intervallo chiuso e limitato [a,b] che assuma valori di segno opposto agli estremi dell’intervallo, condizione che, come detto in precedenza, assicura la presenza di almeno una radice.

Il metodo delle corde (o della falsa posizione), la cui interpretazione grafica è riportata in Fig.1.2, consiste nel calcolare se l’intersezione x_i della retta (corda) passante per i punti A,B di coordinate (a,ƒ(a)) e (b, ƒ(b)) rispettivamente con l’asse delle ascisse è una radice.

Poiché l’equazione di una retta passante per i punti A,B ha equazione:

x  - a    =   y- ƒ(a)
b - a            ƒ(b) -ƒ(a)

ponendo y=0 si ottiene:

x= a -   (b - a)  * f(a)
                ƒ(b) -ƒ(a)
o ancora meglio:

x=   a*f(b) - b* f(a)
            ƒ(b) -ƒ(a)
Per verificare questa condizione, non si controlla se ¦ (x_i  ) = 0, ma (poiché si lavora con i numeri reali) se |¦ (x_i ) | < p, ove p rappresenta la precisione scelta.
Se x_i  non è una radice si valuta il segno del prodotto ¦(a) ^.¦(x_i ) e si procede allo stesso modo nel sottointervallo [a, x_i ] se il segno è negativo, o nel sottointervallo [x_i ,b] se è positivo.

Pertanto iterando il procedimento si genera una successione di termini {x_i}, il cui termine (i+1)-esimo è:

x_i+1 = x_i-1 *f( x_i ) -  x_i * f( x_i-1 )       i= 2,3,4…..
                    ƒ(x_i) - ƒ(x_i-1)

Poiché il procedimento su cui è basato il metodo delle corde approssima la funzione con la retta individuata dai punti di coordinate (a, f(a)) e (b, f(b)) si può dimostrare che l’errore commesso durante ogni iterazione è minore e pertanto è necessario un minor numero di iterazioni, come può essere provato facendo eseguire il programma.

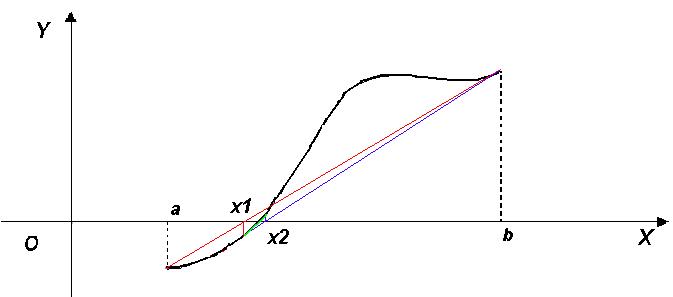
Fig.1.2 Interpretazione geometrica del metodo delle corde