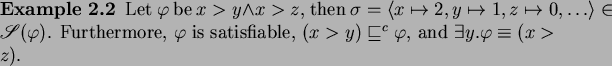Next: The language
Up: Constraint Multiset Rewriting
Previous: Constraint Multiset Rewriting
Constraint Systems
A constraint system is a tup.pngle
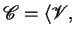
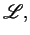
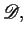
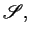
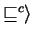 where:
where:
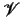 is a denumerable set of variables;
is a denumerable set of variables;
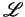 is a first-order language
(the assertional language) defining a set of
formulas with free variables in
is a first-order language
(the assertional language) defining a set of
formulas with free variables in 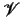 (the constraints),
closed with respect to variable
renaming, existential quantification and conjunction, and allowing
equalities between variables;
(the constraints),
closed with respect to variable
renaming, existential quantification and conjunction, and allowing
equalities between variables;
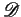 is a possibly infinite set (the interpretation
domain);
is a possibly infinite set (the interpretation
domain);
-
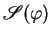 is a set of mappings
is a set of mappings
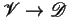 (the
set of solutions of a constraint
(the
set of solutions of a constraint
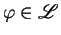 ) that preserves
the usual semantics of equalities,
) that preserves
the usual semantics of equalities, 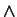 and
and 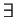 (intersection and projection of the solutions);
(intersection and projection of the solutions);
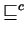 is a relation such that
is a relation such that
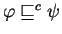 implies
implies
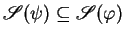 (the entailment relation:
we say that
(the entailment relation:
we say that 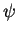 entails
entails 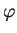 ).
).
We assume that 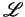 contains constraints, denoted `
contains constraints, denoted `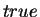 ', and
`
', and
`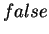 ', which are identically true and identically false in
', which are identically true and identically false in
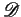 .
By analogy with constraint programming, further requirements on constraint
systems, like solution compactness [22], can be imposed. We refer
to [22] for a discussion.
.
By analogy with constraint programming, further requirements on constraint
systems, like solution compactness [22], can be imposed. We refer
to [22] for a discussion.
In the rest of the paper, we often denote the conjunction between
constraints with a simple comma. We refer to a generic
mapping
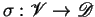 as an evaluation for the
variables in
as an evaluation for the
variables in 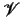 . We use the notation
. We use the notation
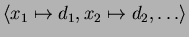 to denote an
evaluation
to denote an
evaluation 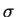 mapping
mapping 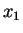 to
to 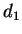 ,
, 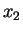 to
to 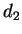 , and so
on, and the notation
, and so
on, and the notation
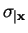 to denote the
restriction of the evaluation
to denote the
restriction of the evaluation 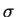 to the variables
to the variables
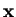 . We also say that a constraint
. We also say that a constraint 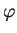 is
satisfiable if
is
satisfiable if
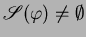 .
.

Note that there exists several methods for checking satisfiability, entailment, and for
variable elimination (see e.g. [10]) over linear arithmetic constraints.
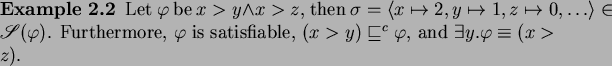
We are now ready to define the framework of multiset rewriting
with constraints.



Next: The language
Up: Constraint Multiset Rewriting
Previous: Constraint Multiset Rewriting
Giorgio Delzanno
2003-02-03