INTRODUZIONE ALLA COMPUTER GRAPHICS

Computer graphics: riguarda tutti gli aspetti di produzione di immagini mediante elaboratore.

Breve storia

Sliluppo della Computer Graphics parallelo a quello della tecnologia hardware.

Inizia con l'introduzione del tubo a raggi catodici (CRT), dispositivo che trasforma impulsi elettrici in immagini, che costituisce i comuni schermi.

Piu' recentemente introdotti gli schermi a cristalli liquidi (LED) usati nei computer portatili.

Grafica vettoriale

Dagli anni '60 fino a meta' degli anni '80.

Un fascio di elettroni mobile colpisce la superficie dello schermo disegnando linee.
E' grafica 2D. Si guida il fascio a disegnare figure.

Grafica raster

Dagli anni '70 in poi.

Lo schermo e' organizzato come una griglia di elementi di immagine o pixel (picture element).
Un fascio di elettroni scandisce lo schermo sequenzialmente riga per riga potendo variare intensita' ad ogni pixel.
E' grafica 2D o 3D. In entrambi i casi prima si traduce la scena in una matrice di pixel (raster) e poi la si trasferisce su schermo.
Per ottenere il colore si usano tre fasci di elettroni per i tre colori primari (rosso, verbe, blu).

Applicazioni della Computer Graphics

Quattro aree principali:

Visualizzazione di informazioni

Uso della comunicazione visuale in sostituzione o aggiunta al linguaggio parlato o scritto.

Progettazione

Uso di strumenti grafici interattivi nella progettazione assistita da calcolatore (CAD).

Simulazione

Generazione di immagini sofisticate in tempo reale.

Interfacce utente

Interazione con l'elaboratore tramite paradigma visuale (finestre, menu', icone...).

Esempi: X Window, Microsoft Windows, Macintosh OS, Netscape

Un sistema grafico

Cinque componenti principali:

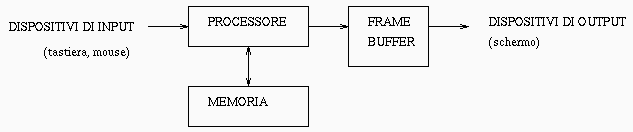
Frame buffer

Area di memoria in genere implementata con chip di memoria speciali (Video Random-Access Memory, VRAM, o Dynamic Random-Access Memory, DRAM).

E' una matrice, controparte in memoria dell'area rettangolare dello schermo (finestra) dove avviene la visualizzazione.

Le dimensioni del frame buffer corrispondono a larghezza ed altezza in pixel della finestra su schermo.

Ospita l'immagine cosi' come e' visualizzata nella finestra.

Il contenuto del frame buffer e' detto matrice o raster di pixel, pixmap (pixel map) o bitmap.

In genere il frame buffer e' composto da piu' buffer, fra cui Spesso finestre grafiche hanno double buffer: Il programma disegna nel back buffer e poi scambia i due buffer in modo da visualizzare istantaneamente quanto disegnato. Invece nelle finestre con single buffer il programma disegna direttamente nel front buffer, e siccome disegnare richiede un certo tempo, questo produce un effetto visivo sgradevole.

Elaborazione grafica

Alcuni sistemi grafici hanno hardware specializzato per certe funzioni grafiche.

Librerie grafiche

Forniscono funzionalita' relative a:

Fasi dell'elaborazione

Due fasi:

Modellazione

Compiuta dal programmatore che scrive il codice dell'applicazione grafica.

Il programmatore specifica la geometria degli oggetti da visualizzare mediante primitive geometriche.

Le primitive geometriche corrispondono a oggetti elementari (in 2D o in 3D) che il sistema "conosce". Sono espresse in forma vettoriale (linee, cerchi, poligoni...).

Assieme alla geometria il programmatore imposta informazioni accessorie che influiranno sulla resa grafica delle primitive:

Visualizzazione (o rendering)

Compiuta dal sistema grafico elaborando le primitive, gli attributi e le trasformazioni. Tramite calcoli, il sistema grafico genera un'immagine raster (determina i valori di colore per i pixel nel frame buffer).
La conversione di primitive vettoriali 2D in immagine raster e' detta rasterizzazione o scan conversion.

Nella grafica 3D, prima della rasterizzazione si ha una traduzione da 3D a 2D fatta in base alla posizione dell'osservatore e alle proprieta' della telecamera. E' un processo complesso che passa attraverso varie fasi. La rasterizzazione avviene solo alla fine.

Stato di un sistema grafico

Attributi e trasformazioni sono parte dello stato del sistema, non sono associati alle primitive.
Non e' una primitiva che e' rossa, ma e' il sistema che sta disegnando con il rosso!

Il codice e' un'alternanza di:

Durante il flusso di esecuzione: Nei sistemi grafici esiste la possibilita' di salvare lo stato corrente per poi ripristinarlo, dopo averlo modificato.
Es: cambiare il colore in rosso, disegnare qualcosa (che sara' rosso) e poi tornare al colore di prima (qualsiasi esso fosse) per disegnare quel che segue.

Colore

Il colori sono espressi in un sistema di riferimento detto spazio o modello dei colori (color space o color model).

Si specifica come formare un colore mischiando alcuni colori considerati primari:

Modello R G B

Modello di colore additivo in cui si considerano tre colori primari (rosso, verde, blu) che sono mischiati per formare il colore desiderato.

Un colore C e' definito come somma pesata di tre componenti:
C = T1 R + T2 G + T3 B dove
R = red, G = green, B = blue, e Ti = intensita' di colore.

A seconda del sistema, le intensita' Ti possono essere espresse

con la convenzione che Possiamo vedere un colore come un punto nel cubo dei colori:
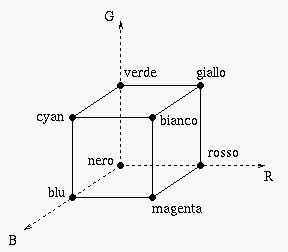nero = (0,0,0)
bianco = (1,1,1)
rosso = (1,0,0)
verde = (0,1,0)
blu = (0,0,1)
giallo = (1,1,0)
ciano = (0,1,1)
magenta = (1,0,1)

Tutti i colori sulla diagonale = toni di grigio.

Modello R G B A

Estensione del modello RGB con componente A detta alpha channel. Il valore di A corrisponde a livello di opacita' o trasparenza, convenzionalmente: In 2D permette di disegnare immagini con sfondo trasparente.
In 3D permette di disegnare oggetti semitrasparenti (es: vetro).

Trasformazioni di coordinate

Permettono di spostare, cambiare dimensioni, deformare le primitive prima di disegnarle.

Trasformazioni affini

Traslazioni, rotazioni, scalature.

Sono trasformazioni rigide: mantengono rette le linee rette e parallele le linee parallele.

I nostri oggetti (primitive geometriche) sono descritti in termini di vertici, basta applicare la trasformazione ai vertici.

Coordinate omogenee

Usate dentro al sistema grafico invece delle coordinate cartesiane.

Vantaggi delle coordinate omogenee:

Traslazione

Traslare un punto = spostarlo di una certa distanza in una certa direzione.
Traslare un oggetto = traslare solidalmente tutti i suoi punti.

Parametro = vettore di traslazione (tx,ty) in 2D e (tx,ty,tz) in 3D.

In 2D: Dato un punto P = (x,y), il punto traslato e' P' = (x+tx,y+ty) = (x,y) + (tx,ty).
In 3D: Dato un punto P = (x,y,z), il punto traslato e' P' = (x+tx,y+ty,z+tz) = (x,y,z) + (tx,ty,tz).

In coordinate omogenee e forma matriciale (provare per credere):
In 2D: 
[x']    [1 0 tx] [x]
[y']  = [0 1 ty] [y]
[1]     [0 0 1 ] [1]
In 3D: 
[x']    [1 0 0 tx] [x]
[y']  = [0 1 0 ty] [y]
[z']    [0 0 1 tz] [z]
[1]     [0 0 0 1 ] [1]
Nota: la traslazione inversa corrisponde al vettore di traslazione cambiato di segno (-tx,-ty) in 2D e (-tx,-ty,-tz) in 3D.

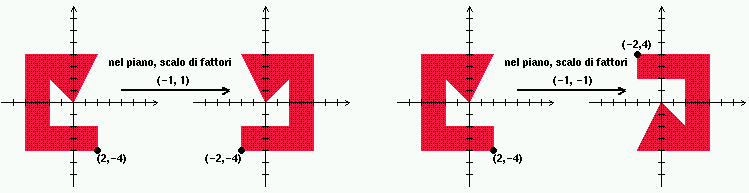
Scalatura

Scelto un punto C che rimane fermo, scalare un punto = riposizionarlo ricalcolando le sue distanze (nella direzione di ciascun asse coordinato) da C in base ad una nuova unita' di misura.
Scalare un oggetto = scalare (riposizionare rispetto al punto fermo C) tutti i suoi punti.

Vediamo scalatura con punto fermo l'origine.

Parametri = fattori di scala (sx,sy) in 2D e (sx,sy,sz) in 3D, uno per ogni asse del sistema di riferimento.

In 2D: Dato un punto P = (x,y), il punto scalato e' P' = (sx*x,sy*y).
In 3D: Dato un punto P = (x,y,z), il punto scalato e' P' = (sx*x,sy*y,sz*z).

In coordinate omogenee e forma matriciale (provare per credere):
In 2D: 
[x']    [sx 0  0] [x]
[y']  = [0  sy 0] [y]
[1]     [0  0  1] [1]
In 3D: 
[x']    [sx 0  0  0] [x]
[y']  = [0  sy 0  0] [y]
[z']    [0  0  sz 0] [z]
[1]     [0  0  0  1] [1]
La scalatura inversa si ottiene prendendo l'inverso dei fattori di scala: 1/sx, 1/sy, 1/sz.

La scalatura tenendo fermo un punto generico C diverso dall'origine si ottiene come combinazione di trasformazioni (ved. dopo).

Nota: se i fattori di scala sono negativi, ottengo una riflessione speculare.

Rotazione

In 2D: scelto un punto R ed un verso di rotazione (orario o antiorario), ruotare un punto = muoverlo attorno ad R di un certo angolo nel verso assegnato.
In 3D: scelta una retta r (asse di rotazione) ed un verso di rotazione, ruotare un punto = muoverlo attorno ad r di un certo angolo nel verso assegnato.

Ruotare un oggetto = muovere ciascun punto dell'oggetto solidalmente dello stesso angolo attorno al punto R (in 2D) o alla retta r (in 3D) nel verso assegnato.


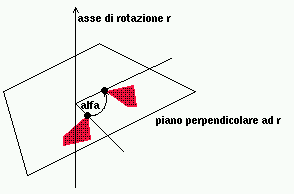
La rotazione 2D corrisponde alla rotazione in 3D attorno a un asse passante per il punto R e parallelo all'asse z.

Vediamo:

Parametri di questo specifico caso (sia in 2D che in 3D): angolo di rotazione alfa (alfa > 0 per senso antiorario, alfa < 0 per senso orario).

In 2D: Dato un punto P = (x,y), il punto ruotato e' P' = (x',y')
In 3D: Dato un punto P = (x,y,z), il punto ruotato e' P' = (x',y',z')
dove:


In coordinate omogenee e forma matriciale (provare per credere):
In 2D: 
[x']    [cos(alfa)  -sin(alfa)  0] [x]
[y']  = [sin(alfa)   cos(alfa)  0] [y]
[1]     [0           0          1] [1]
In 3D: 
[x']    [cos(alfa)  -sin(alfa)  0 0] [x]
[y']  = [sin(alfa)   cos(alfa)  0 0] [y]
[z']    [0           0          1 0] [z]
[1]     [0           0          0 1] [1]
Nota: e' uguale alla matrice identita' eccetto per le prime due righe e colonne (quelle corrispondenti alle coordinate x ed y).

In 3D: Analogamente le matrici di rotazione per rotazione attorno all'asse x ed y sono uguali all'identita' tranne per le righe e colonne corrispondenti alle coordinate yz e xz.

In 3D: La matrice di rotazione per rotazione attorno ad una retta generica passante per l'origine ha forma piu' complicata, che non vediamo.

La rotazione inversa si ottiene con l'angolo di rotazione cambiato di segno.

La rotazione attorno ad un punto diverso dall'origine (in 2D) e attorno ad una retta non passante per l'origine (in 3D) si ottengono come combinazioni di trasformazioni (ved. dopo).

Composizione di trasformazioni

Tutte le trasformazioni rigide si ottengono per composizione a partire da un insieme minimale di trasformazioni di base: Composizione (o concatenazione) = eseguire le trasformazioni in sequenza.

Sequenza di trasformazioni = moltiplicazione in sequenza delle rispettive matrici.

L'ordine da sinistra a destra in cui scrivo le matrici nella moltiplicazione e' opposto all'ordine in cui applico le trasformazioni.

Se P e' un punto, ed M1, M2 sono due matrici di trasformazione, la moltiplicazione M1 M2 P applica a P prima M2 e poi M1.

Esempio: Scalatura tenendo fermo un punto generico

Vediamo direttamente il caso 3D (il 2D corrisponde a dimenticare la coordinata z).

Sia C=(x0,y0,z0) il punto che deve restare fermo.

Esempio: Rotazione attorno ad un asse passante per un punto generico

Si fa in modo analogo alla scalatura.

Proprieta' della composizione di trasformazioni

Come la moltiplicazione di matrici, in generale non e' commutativa. Esempio:


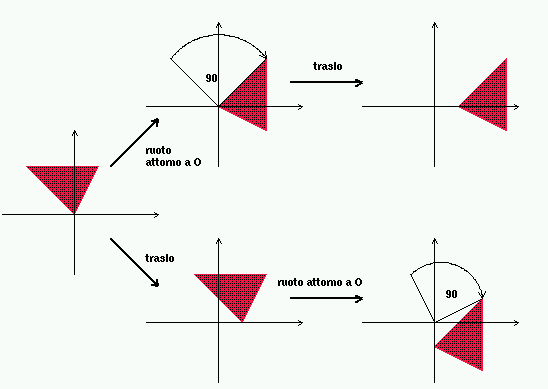
La composizione di trasformazioni dello stesso tipo e' commutativa (traslazioni con traslazioni, scalature con fermo lo stesso punto, rotazioni attorno allo stesso asse).