TRASFORMAZIONI DI COORDINATE
Coordinate omogenee
Usate dentro al sistema grafico invece delle coordinate cartesiane.
-
Un punto e' descritto da una terna di coordinate cartesiane P = (X,Y,Z).
-
Lo stesso punto e' descritto da infinite quadruple di
coordinate omogenee P = (x,y,z,w), tutte quelle per cui
- w < > 0
- x/w = X
- y/w = Y
- z/w = Z
-
Rappresentazione canonica: w=1, dunque P = (X,Y,Z,1).
Le quadruple di coordinate omogenee con w=0, cioe' della forma
(x,y,z,0) identificano punti all'infinito nella direzione del vettore
(x,y,z).
Vantaggi dell'uso di coordinate omogenee:
-
Consentono di rappresentare punti all'infinito (con w=0).
Es: sorgenti luminose.
-
Consentono di esprimere tutte le trasformazioni di coordinate in
forma matriciale (ved. dopo).
Il sistema memorizza una trasformazione (di modellazione, di vista,
di proiezione) in una matrice M (matrice 4x4).
Dato un punto P (vettore di 4 elementi), il risultato di
applicare la trasformazione a P
e' dato da P' = M P (moltiplicazione matrice vettore).
Trasformazioni di modellazione
Traslazioni, rotazioni, scalature per posizionare un oggetto all'interno
della scena.
Sono trasformazioni rigide (mantengono le proporzioni fra
le parti dell'oggetto).
Poiche' i nostri oggetti (primitive geometriche) sono descritti in
termini di vertici, basta applicare la trasformazione ai vertici.
Traslazione
Traslare un oggetto = traslare solidalmente tutti i suoi punti.
Traslare un punto = spostarlo di una certa distanza in una certa
direzione.
Parametro = vettore di traslazione (tx,ty,tz).
Se P = (x,y,z) e' un punto, il punto traslato e'
P' = (x+tx,y+ty,z+tz) = (x,y,z) + (tx,ty,tz).
In coordinate omogenee e forma matriciale (provare per credere):
[x'] [1 0 0 tx] [x]
[y'] = [0 1 0 ty] [y]
[z'] [0 0 1 tz] [z]
[1] [0 0 0 1 ] [1]
Nota: la traslazione inversa corrisponde al vettore di traslazione
inverso (-tx,-ty,-tz).
Scalatura
Scalare un oggetto = scegliere un punto C che rimane fermo e riposizionare
ciascun punto dell'oggetto ricalcolando le sue distanze da C
(nella direzione di ciascun asse coordinato) in base ad
una nuova unita' di misura.
Adesso vediamo scalatura con punto fermo l'origine.
Parametri = fattori di scala (sx,sy,sz), uno per ogni asse del sistema
di riferimento.
Se P = (x,y,z) e' un punto, il punto scalato e'
P' = (sx*x,sy*y,sz*z).

In coordinate omogenee e forma matriciale (provare per credere):
[x'] [sx 0 0 0] [x]
[y'] = [0 sy 0 0] [y]
[z'] [0 0 sz 0] [z]
[1] [0 0 0 1] [1]
La scalatura tenendo fermo un punto generico C diverso dall'origine si
ottiene come combinazione di trasformazioni (ved. dopo).
Nota: se i fattori di scala sono negativi, ottengo una riflessione
speculare.
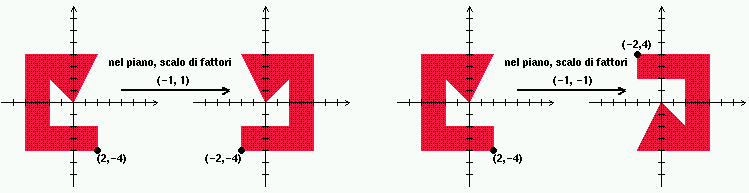
Rotazione
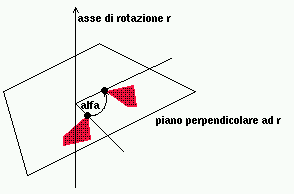
Ruotare un oggetto = scegliere un asse di rotazione (una retta r)
ed un verso di rotazione, e muovere ciascun punto dell'oggetto
solidalmente dello stesso angolo attorno ad r nel verso assegnato.
Nota: anziche' una retta ed un verso di rotazione, posso dare una
retta orientata (il verso di rotazione e' quello che appare antiorario
guardando nella direzione opposta a quella della retta).
Adesso vediamo rotazione attorno ad uno degli assi coordinati,
per esempio l'asse z.
Parametri: angolo di rotazione alfa (alfa > 0 per senso
antiorario, alfa < 0 per senso orario).
Se P = (x,y,z) e' un punto, il punto ruotato e'
P' = (x',y',z') dove:
- x' = x*cos(alfa) - y*sin(alfa)
- y' = x*sin(alfa) + y*cos(alfa)
- z' = z

In coordinate omogenee e forma matriciale (provare per credere):
[x'] [cos(alfa) -sin(alfa) 0 0] [x]
[y'] = [sin(alfa) cos(alfa) 0 0] [y]
[z'] [0 0 1 0] [z]
[1] [0 0 0 1] [1]
Nota: e' uguale alla matrice identita' eccetto per le prime due
righe e colonne (quelle corrispondenti alle coordinate x ed y).
Analogamente le matrici di rotazione per rotazione attorno all'asse
x ed y sono uguali all'identita' tranne per le righe e colonne
corrispondenti alle coordinate yz e xz.
La matrice di rotazione per rotazione attorno ad una retta generica
passante per l'origine ha forma piu' complicata, che non vediamo.
La rotazione attorno ad una retta non passante per l'origine si
ottiene come combinazione di trasformazioni (ved. dopo).
Composizione di trasformazioni
Un sistema grafico (es:OpenGL) fornisce istruzioni per definire:
- traslazioni dato il vettore di traslazione (tx,ty,tz)
- scalature con punto fermo l'origine dati i fattori di
scala (sx,sy,sz)
- rotazioni attorno ad una retta passante per l'origine
dato l'angolo di rotazione alfa ed un vettore (rx,ry,rz)
parallelo all'asse di rotazione
Tutte le altre trasformazioni rigide si ottengono per composizione
di queste.
Composizione = eseguire le trasformazioni in sequenza.
Sequenza di trasformazioni = moltiplicazione in sequenza delle rispettive
matrici.
L'ordine da sinistra a destra in cui scrivo le matrici nella moltiplicazione
e' opposto all'ordine in cui applico le trasformazioni.
Se P e' un punto, ed M1, M2 sono due matrici di trasformazione,
la moltiplicazione M1 M2 P applica a P prima M2 e poi M1.
Scalatura tenendo fermo un punto generico
Sia C=(x0,y0,z0) il punto che deve restare fermo.
- Traslo per portare C nell'origine:
traslo di vettore (-x0,-y0,-z0)
- Scalo con i fattori di scala assegnati
- Traslo per portare l'origine in C (cioe' far tornare
C al suo posto): traslo di vettore (x0,y0,z0)
Rotazione attorno ad un asse passante per un punto generico
Si fa in modo analogo.
Proprieta' della composizione di trasformazioni
Come la moltiplicazione di matrici, in generale non e'
commutativa.
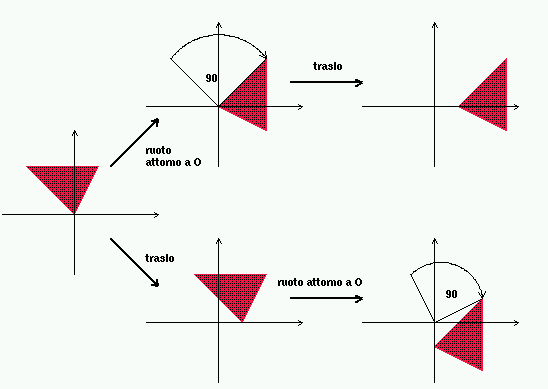
La composizione di trasformazioni dello stesso tipo e' commutativa
(traslazioni con traslazioni,
scalature con fermo lo stesso punto,
rotazioni attorno allo stesso asse).
Trasformazioni di vista
Suppongo di sapere, espresse in coordinate del mondo:
- la posizione del punto di vista V = (vx,vy,vz)
- i versori dei tre assi del sistema di riferimento
dell'occhio i = (ix,iy,iz), j = (jx,iy,jz), k = (kx,ky,kz)
Primo modo: lo faccio a mano
Costruisco la trasformazione che posiziona la scena davanti alla
telecamera, ovvero che porta la scena da coordinate del mondo
a coordinate dell'occhio.
Questa trasformazione e' una combinazione di traslazioni e
rotazioni.
Dato un punto P espresso in coordinate di vista, voglio trovare
le coordinate di P espresse in coordinate dell'occhio.
-
Traslazione che porta V nell'origine: vettore di traslazione
(-vx,-vy,-vz).
Esempio: se la mia scena e' centrata nell'origine di WC e voglio
vederla da V = (10,0,0) la traslo indietro di 10 unita' lungo
l'asse x.
-
Rotazione che porta gli assi x,y,z dell'occhio a coincidere con
gli assi x,y,z di WC.
Matrice di rotazione:
[ix iy iz 0] versore asse x
[jx jy jz 0] versore asse y
[kx ky kz 0] versore asse z
[0 0 0 1]
Secondo modo: lo faccio fare al sistema
Il sistema (es: OpenGL) fornisce una funzione che permette di specificare
una trasformazione di vista dando:
-
le coordinate V = (vx,vy,vz)
dell'occhio nel sistema WC (view reference point):
sara' l'origine del sistema dell'occhio
-
le coordinate del centro della scena C, che assieme a V determina la
direzione di vista come la direzione del vettore VC:
sara' l'asse z negativo del sistema dell'occhio
(invece CV e' la normale al piano di vista, view plane normal)
-
un vettore non parallelo a VC, la cui componente perpendicolare a
VC determina la direzione dell'alto (view up vector):
sara' l'asse y del sistema dell'occhio
Manca un asse (asse x) del sistema dell'occhio: il sistema lo calcola
automaticamente come il prodotto vettoriale dei due assi noti.
Quando conviene usare l'uno o l'altro modo
In generale e' difficile costruire a mano la rotazione.
Puo' essere facile in casi particolari.
Esempio:
-
la direzione di vista e' parallela ad uno degli assi coordinati di WC
(basta una rotazione attorno a quell'asse per portare gli altri due
assi in posizione)
-
gli angoli di rotazione sono gestiti interattivamente dall'interfaccia
utente
Esempio:
Nel programma Simple3D.java
il punto di vista puo' orbitare attorno alla scena in base a due angoli
(latitudine, longitudine) controllati dall'utente.
La scena in coordinate del mondo e' centrata nell'origine.
La trasformazione di vista consiste in:
rotazione attorno all'asse z (di angolo longitudine), rotazione
attorno all'asse x (di angolo latitudine), traslazione per portare
il punto di vista ad una certa distanza dalla scena.
In questo caso usare il secondo modo sarebbe
piu' complicato perche' dovrei calcolare a mano la posizione del punto
di vista in coordinate del mondo con funzioni trigonometriche.
Nota: il programma richiede anche il file
BasicGL.java (usato negli esercizi di
laboratorio).
Le rotazioni si ottengono muovendo il mouse con il testo premuto
all'interno della finestra grafica.
Trasformazioni di proiezione
-
Proiezione parallela: proietta con un fascio di rette parallele,
mantiene le proporzioni relative tra gli oggetti.
-
Proiezione prospettica: proietta con un fascio di rette centrate
in un punto, non le mantiene le proporzioni (amplifica gli
oggetti vicini, riduce quelli lontani).
-
Proiezione ortografica: caso particolare
di proiezione parallela dove il fascio
di rette e' perpendicolare al piano di proiezione.
Vediamo solo le seconde due (sono quelle disponibili in OpenGL).
Proiezione ortografica
In un sistema grafico definita fornendo un volume di vista
che e' un parallelepipedo retto con facce allineate con le
direzioni dei piani coordinati del sistema di riferimento dell'occhio.
Tale parallelepipedo e' descritto dalle sue coordinate
xyz minime e massime.
- x fra left e right
- y fra bottom e top
- z fra near e far
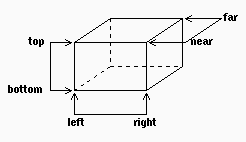
Il parallelepipedo viene traslato e scalato per coincidere con il cubo NPC.
Proiezione prospettica
In un sistema grafico definita fornendo, in coordinate dell'occhio,
un volume di vista
che e' un tronco di piramide le cui facce laterali convergono
nel punto di vista (= origine), e le cui basi sono parallele al
piano xy dell'occhio.
- sulla base minore del tronco di piramide, le x sono fra left e right
- sulla base minore del tronco di piramide, le y sono fra bottom e top
- le z del tronco di piramide sono fra near e far
L'intervallo delle x e delle y sulla base maggiore del tronco di piramide
si desumono a partire dalle informazioni di cui sopra.
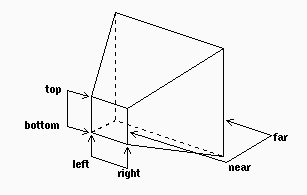
Il tronco di piramide viene deformato (dilatando la parte vicina,
restringendo la parte lontana) per coincidere con il cubo NPC.
Non e' una trasformazione rigida!
Come si deformano gli oggetti
Vediamo come si deformano le coordinate x,y in una
trasformazione prospettica.
O = punto di vista (origine), P = (x,y,z) = punto nel volume di vista.
Nella trasformazione, il punto P riceve le stesse coordinate x ed y di
tutti i punti
giacenti sulla retta congiungente OP, in particolare le stesse coordinate
del punto P' = (x',y',near) intersezione di OP con la base minore
della piramide.
Vediamo per esempio la coordinata y.
In figura la sezione con piano di taglio il piano x=0:
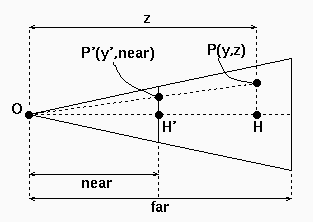
Il rapporto fra y' ed y dice quanto la y di P viene compressa/dilatata.
Sfruttando la similitudine fra i triangoli OHP e OH'P' otteniamo
y' = y * near/z
Piu' P e' vicino al punto di vista (z minore) e piu' la y viene dilatata.
Analogamente la x si ottiene x' = x * near/z
Poi viene eseguita la normalizzazione per ridurre l'intervallo dei
valori delle coordinate fra -1 ed 1.








