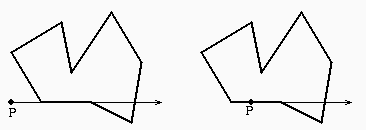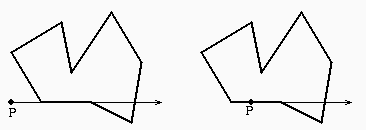Dispense di I.U.M. Modellazione Geometrica

Leila De Floriani, Paola Magillo

Cap.4: Localizzazione di un punto

[Riferimento: cap.2 del libro di Preparata e Shamos]

Localizzazione di un punto in un poligono semplice

(Problema detto anche point location o point-in-polygon)

Consideriamo:

Formulazione del problema

Dato un poligono semplice Pigreco ed un punto P, determinare se P e' interno a Pigreco.

P e' detto interno a Pigreco sse P appartiene alla regione poligonale chiusa contornata da Pigreco.

Algoritmo

Definiamo un algoritmo che risolve il problema del point-location in tempo O(N) e senza preprocessing, per un poligono con N vertici.

Idea

Applicazione del teorema di Jordan.

Teorema di Jordan: una curva chiusa e semplice divide il piano in due regioni (interno ed esterno) che hanno in comune il contorno.

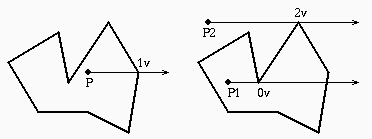
Consideriamo una semiretta orizzontale l' con origine nel punto P e diretta verso destra. Contiamo quante volte l' attraversa il poligono. Ogni volta che attraverso il poligono passo dall'esterno all'interno o viceversa. Alla fine (all'infinito) devo essere all'esterno.

Operativamente, intersechiammo la semiretta con ciascun lato del poligono. Dobbiamo gestire consistentemente i due casi particolari: Se un lato orizzontale e' completamente contenuto nella semiretta, puo' essere ignorato: la risposta all'interrogazione non cambia se immaginiamo di contrarre quel lato ad un punto.

Se un lato orizzontale e' solo parzialmente sovrapposto alla semiretta, vuol dire che ne contiene il punto iniziale P. Quindi, appartenendo ad un lato, P appartiene al poligono.

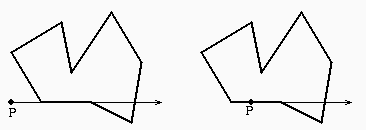
Se la semiretta passa per un vertice V del poligono, e i due lati di Pigreco che condividono il vertice V giacciono uno al di sopra e l'altro al di sotto di l', allora l'intersezione va contata una sola volta (solo per uno dei due lati che intervengono, per es. quello sottostante).

Se la semiretta passa per un vertice V, e i due lati che condividono V giacciono entrambi al di sopra oppure entrambi al di sotto di l', allora l'intersezione non va contata, oppure va contata due volte.

Tirando le somme, per ogni e lato di Pigreco:

  1. Se e e' orizzontale:
    Si controlla se P e' interno ad e (inteso come segmento chiuso). In caso affermativo concludiamo subito che P e' interno, altrimenti ignoriamo il lato e.
  2. Se e non e' orizzontale:
    Si controlla se l' interseca e. In caso affermativo, l'intersezione viene contata solo se e' interna ad e, oppure se coincide con il suo vertice estremo di ordinata maggiore.

Pseudocodice

Algorithm POINT_LOCATION (Pigreco,P,l')
 Pigreco: poligono 
 P: punto (query point)
 l': semiretta passante per P (orizzontale)
begin
 count := 0 (* contatore del numero di intersezioni *)
 for i:=1 to N do
  begin
   (* nel seguito edge(i) indica l'i-esimo lato di Pigreco *)
   if edge(i) non e' orizzontale
   then 
     if edge(i) interseca l' in un punto interno o nel vertice
        estremo di ordinata maggiore
     then
       count := count + 1
   else (* edge(i) e' orizzontale *)
     if edge(i) contiene P
     then return "P e' interno a Pigreco"
   end (* ciclo for *)
 if count e' dispari
 then return "P e' interno a Pigreco"
 else return "P e' esterno a Pigreco"
end (* POINT_LOCATION *)

Analisi dell'algoritmo

Complessita' spaziale (storage): O(N) per la memorizzazione del poligono.

Complessita' temporale dell'interrogazione (query time): O(N) in quanto la semiretta deve essere intersecata con ogni lato non orizzontale del poligono.

Nessun preprocessing time.

Localizzazione di un punto in un poligono convesso

Caso particolare di poligono in cui vale la seguente proprieta' (che sfrutteremo nell'algoritmo).

Proprieta'

I vertici di un poligono convesso sono ordinati in modo angolare rispetto ad un qualunque punto interno.

Idea dell'algoritmo

Dividere il poligono convesso Pigreco in settori considerando un punto interno Q e gli N raggi uscenti da Q e passanti per i vertici di Pigreco.

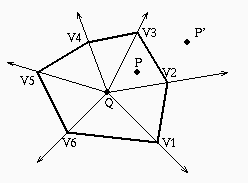
Ogni settore e' suddiviso da un lato di Pigreco in due parti: una interna a Pigreco ed una esterna.

Dato un punto P, si tratta di:

  1. localizzare P nel settore cui appartiene
  2. stabilire da che parte giace P rispetto al lato del poligono che appartiene al settore di P

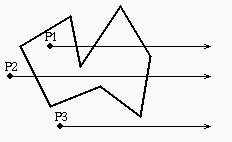
    Passo 1

    Si considera un sistema di coordinate polari centrato in Q e si effettua una ricerca binaria sui settori definiti dal punto Q con i punti V(i) vertici di Pigreco.

    Nell'esempio per trovare il settore del punto P analizziamo i settori V1V4, V2V4, V2V3.

    Controllo se P appartiene al settore definito dai raggi passanti per V(i) e V(j):

    1. se l'angolo V(i)QV(j) e' minore di 180 gradi (cioe' se V(i)QV(j) definisce una svolta a destra), allora P appartiene al settore sse
      • l'angolo PQV(j) definisce una svolta a destra
        AND
      • l'angolo PQV(i) definisce una svolta a sinistra
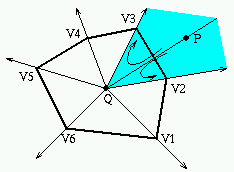
    2. se l'angolo V(i)QV(j) e' maggiore di 180 gradi (cioe' se V(i)QV(j) definisce una svolta a sinistra), allora P appartiene al settore sse P non appartiene al settore supplementare (che e' minore di 180), ovvero sse
      • l'angolo PQV(i) definisce una svolta a sinistra
        OR
      • l'angolo PQV(j) definisce una svolta a destra

    Passo 2

    Sappiamo che P appartiene al settore definito dai raggi passanti per V(i) e V(i+1):
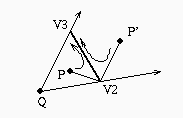
    Nota: P appartiene al poligono se P e' interno al segmento V(i)V(i+1).

    Valutazione dell'algoritmo

    Preprocessing time: O(1), poiche' un punto interno si trova in tempo costante (baricentro dei primi tre vertici) e il contorno di Pigreco e' gia' dato ordinato radialmente rispetto a qualunque punto interno.

    Query time: O(log N) determinato dal costo della ricerca binaria su N settori.

    Storage: O(N) per i lati del poligono.

    Esercizio

    Quale struttura dati si puo' utilizzare per ottenere query time in O(log N)?

    Estensione per poligoni a stella

    L'algoritmo sopra descritto per poligono convessi funziona anche per alcuni poligoni non convessi La proprieta' dell'ordinamento angolare e' valida anche per poligoni a stella (star-shaped).

    Definizione

    Un poligono semplice Pigreco e' detto poligono a stella sse esiste un punto Q non esterno a Pigreco tale che per ogni punto P di Pigreco il segmento PQ e' completamente interno a Pigreco.

    Il luogo dei punti Q che soddisfano la proprieta' di cui sopra e' detto nucleo di Pigreco.

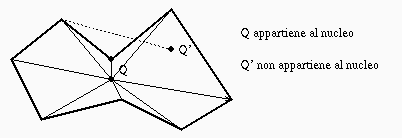
    L'algoritmo di point location per poligoni convessi puo' essere esteso ad un poligono Pigreco star-shaped scegliendo come punto Q un punto del nucleo di Pigreco.

    Quindi per poligoni a stella il problema del point location puo' essere risolto in

    Nucleo di un poligono star-shaped

    Intersezione degli N semipiani (orientati) definiti dagli N lati del poligono.

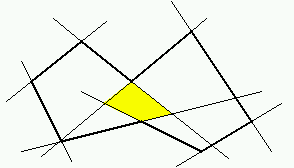
    Ogni semipiano definisce una zona in cui deve giacere il nucleo del poligono.

    Esistono algoritmi per la determinazione del nucleo di complessita' O(N) (ved. cap.7 Preparata e Shamos).

    Localizzazione di un punto in una suddivisione piana

    Formulazione del problema

    Sia Sigma = (V,E,F) una suddivisione piana. Dato un punto P nel piano, determinare la faccia f in F o lo spigolo e in E contenente P, o il vertive v in V che coincide con P.

    Metodi di soluzione

    Vediamo due metodi:
    1. Metodo diretto (senza pre-elaborazione)
    2. Metodo delle strisce (slab method) [cap.2 libro di Preparata e Shamos] che prevede una fase di pre-elaborazione con costruzione di un indice spaziale

    Metodo diretto

    Schema generale dell'algoritmo: 
    Algorithm DIRECT_POINT_LOC (P)
  for every f faccia interna in F
    Pigreco := il poligono definito da FV(f)
    case ( point-in-polygon(P,Pigreco,e,v) )
      INSIDE: return f;
      ONEDGE: return e;
      ONVERTEX: return v;
    end case
  end for
  f := faccia esterna
  return f
    La procedura point-in-polygon implementa l'algoritmo di localizzazione di un punto in un poligono semplice. Essa restituisce un valore simbolico che descrive la situazione del punto rispetto al poligono:

    Complessita' temporale

    La struttura dati per la codifica di Sigma va scelta in modo tale che la relazione FV(f) sia ricavabile in tempo lineare in #FV(f).
    In questo caso, la complessita' temporale e' in O(#V) in quanto ogni spigolo della suddivisione piana viene considerato in esattamente due poligoni, e, all'interno della procedura point-in-polygon, ogni spigolo del poligono e' intersecato una volta con la semiretta orizzontale. Ne segue un numero di operazioni pari a 2(#E), cioe' in O(#V) per la formula di Eulero.

    NOTA: il metodo NON richiede pre-elaborazione.

    Metodo delle strisce (Slab method)

    [Dobkin e Lipton, 1976; ved. anche Preparata e Shamos, cap.2]

    Idea

    Sovrapporre alla suddivisione piana Sigma=(V,E,F) un indice spaziale (struttura dati) che permetta di effettuare la localizzazione di un punto in tempo O(log N) dove N=#V.

    Descrizione dell'indice spaziale

    Data Sigma dividiamo il piano in al piu' N+1 strisce orizzontali o verticali, di cui due non intersecano Sigma. Si considerano solo le strisce che intersecano Sigma (al piu' N-1).

    Nel seguito supponiamo una suddivisione in strisce verticali.

    Per localizzare un punto P=(x,y) si compie una ricerca sulle ascisse seguita da una ricerca sulle ordinate, entrambe in O(log N).

    Dato un punto P=(x,y):

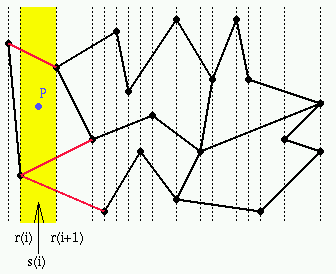
    Struttura dati per codificare indice spaziale e suddivisione

    Per la suddivisione piana

    Si puo' utilizzare una qualunque delle due strutture dati viste (Winged-Edge o simmetrica).

    Nei vari algoritmi osserviamo quale e' l'insieme minimale di relazioni che dobbiamo mantenere nella struttura.

    Per l'indice spaziale

    Il costo della struttura nel caso pessimo e' O(N^2) in quanto abbiamo al piu' N-1 strisce e O(N) segmenti per ciascuna striscia nel caso pessimo.

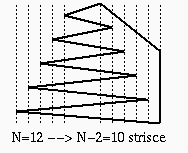
    Nota: non e' possibile ridurre l'occupazione di memoria in quanto esistono suddivisioni piane che producono O(N^2) segmenti (si veda l'esempio illustrato nella figura: suddivisione piana consistente in un solo poligono "a pettine").

    Algoritmo di localizzazione di un punto

    Dato un punto P da localizzare nella suddivisione Sigma:

    Fase 1

    Si localizza la striscia s(i) contenente P effettuando una ricerca nell'array L in base all'ascissa di P.

    Fase 2

    Si localizza la faccia, spigolo o vertice contenente all'interno di s(i).

    Per fare cio' si effettua una ricerca sull'albero T(i) a partire dalla radice:

    • Ad ogni passo si confronta P con il segmento contenuto nel nodo corrente di T(i) allo scopo di stabilire se P giace sopra o sotto tale segmento.
      Il confronto si riduce a controllare se P sta a destra o a sinistra dello spigolo e di Sigma memorizzato nel nodo corrente. Nota bene: se "sopra il segmento" significa "a destra" oppure "a sinistra di e" dipende dall'orientamento dello spigolo e in Sigma.

    • La ricerca termina quando si verifica una delle seguenti condizioni:
      1. P sta sopra o sotto a tutti i segmenti che intersecano la striscia. In questo caso P e' esterno a Sigma.
      2. P e' compreso fra due segmenti consecutivi fra quelli che intersecano la striscia. Siano e' ed e'' i lati di Sigma di cui tali segmenti fanno parte. In questo caso P e' contenuto nella faccia f comune a EF(e') ed EF(e'').
      3. P appartiene ad un segmento fra quelli che intersecano la striscia. Sia e lo spigolo di Sigma di cui tale segmento fa parte. In questo caso P appartiene allo spigolo e. Si deve stabilire se P coincide con uno dei vertici estremi.
    La complessita' dell'algoritmo e' O(log N) in quanto si hanno al piu' N-1 strisce e O(N) spigoli che intersecano una striscia.

    OSSERVAZIONE: Per la localizzazione bastano le relazioni EF ed EV nella struttura di codifica di Sigma.

    Algoritmo per la costruzione dell'indice spaziale

    • INPUT: suddivisione piana Sigma
    • OUTPUT: struttura a strisce S (indice spaziale)

    Metodo brute-force

    1. Ordinamento dei vertici per ascissa non decrescente (vi possono essere piu' vertici con la stessa ascissa).
    2. Eliminazione dei "doppioni", ottenendo quindi un ordinamento per ascissa strettamente crescente dei vertici che rimangono.
    3. Costruzione dell'array di strisce L dalla lista ordinata di vertici cosi' ottenuta.
    4. Per ogni striscia s(i), inizializzare l'albero T(i) come vuoto.
    5. Per ogni spigolo e di Sigma, per ogni striscia s(i) intersecata da e, inserire e in T(i).
    Complessita' temporale: O(N^2 (log N)) poiche' ogni spigolo puo' dover essere inserito in O(N) strisce, e l'inserimento in un albero bilanciato con O(N) nodi richiede O(log N).

    OSSERVAZIONE: L'algoritmo non usa coerenza spaziale fra le strisce e richiede solo che nella struttura di codifica di Sigma sia fornita la relazione EV.

    Metodo con sweep-line

    Sfruttiamo la coerenza spaziale fra strisce consecutive.

    OSSERVAZIONE: Il contenuto di due strisce consecutive differisce solo per segmenti definiti da lati che incidono nei vertici di Sigma che giacciono sulla retta verticale di confine fra le due strisce.

    Adottiamo un processo di plane-sweep: "spazzamento" del piano mediante una retta (detta sweep-line) orizzontale o verticale che si muove con continuita' sul piano.

    In ogni sua posizione, la sweep-line e' caratterizzata da uno stato. Durante il moto della sweep-line, il suo stato cambia in corrispondenza di certi punti detti eventi.

    Nel nostro caso consideriamo una sweep-line verticale che si muove da sinistra verso destra.

    • Lo stato e' l'insieme degli spigoli di Sigma intersecati dalla sweep-line alla posizione corrente, ordinati dal basso verso l'alto.
    • Gli eventi sono i vertici della suddivisione piana Sigma.
    In corrispondenza degli eventi cambia l'insieme degli spigoli di Sigma intersecati dalla sweep-line, in altre parole lo stato cambia in corrispondenza di tutti e soli i vertici di Sigma.

    In corrispondenza di una striscia s(i) l'albero T(i) che ne descrive il contenuto e' ottenuto copiando lo stato della sweep-line quando questa e' all'interno della striscia s(i).

    La coda degli eventi puo' essere un array poiche' tutti gli eventi sono noti a priori.
    Lo stato della sweep-line deve essere rappresentato mediante un albero bilanciato T.

    Schema dell'algoritmo:

    1. Ordinamento dei vertici di Sigma per ascissa non decrescente ed inizializzazione dell'array E che rappresenta la coda degli eventi.

    2. Per ogni vertice v:
      • Sia VE(v) la lista dei suoi spigoli incidenti.
      • Si suddivide VE(v) in due liste VE1(v) e VE2(v) che contengono rispettivamente gli spigoli entranti e uscenti da v. Uno spigolo e' definito entrante in v se v e' l'estremo di v avente ascissa massima; e' definito uscente in caso contrario. Si noti che uno fra VE1(v) e VE2(v) puo' essere vuoto.

    3. Sia L l'array che definisce l'indice spaziale. 
       i := 1; (* prossima striscia da inizializzare *)
 T := albero vuoto; (* sweep-line status *)
 for j = 1 to N do (* j = cursore sull'array degli eventi *)
   P := E[j]; (* evento corrente *)
   for every e in VE1(P) DELETE(T,e);
   for every e in VE2(P) INSERT(T,e);
   if j < N AND E[j+1] ha ascissa maggiore di P
   then begin
         associa P alla striscia L[i];
         copia T in T(i);
         i = i+1; (* prossima striscia *)
        end if
 end for
    Complessita' temporale: O(N^2) nel caso peggiore in quanto dominata dall'operazione di copiatura di T in T(i).

    L'algoritmo tratta correttamente anche il caso di piu' vertici appartenenti alla stessa retta verticale.