I.U.M. Modellazione Geometrica
Laboratorio di I.U.M. Modellazione Geometrica
Esercizio 1
Scrivere un algoritmo per convertire una regione
da una rappresentazione
secondo il contorno ad una rappresentazione secondo lo spazio occupato,
più precisamente a griglia di pixel.
La regione e' una regione poligonale semplicemente connessa.
-
INPUT:
una lista di punti (ciascun punto una coppia di coordinate)
t.c., connettendo ogni punto al successivo, e l'ultimo al primo,
si ottiene il poligono di contorno della regione
ordinato in senso antiorario.
Le coordinate dei vertici sono numeri floating point.
-
OUTPUT:
una griglia
(matrice) di pixel ciascuno dei quali e' marcato come pieno (valore 1)
se ha intersezione non nulla con la regione, e vuoto (valore 0) altrimenti.
Convenzioni:
-
I pixel hanno lato di lunghezza unitaria e
i vertici della griglia hanno coordinate intere.
-
Le coordinate dei vertici del poligono hanno parte decimale non nulla.
In questo modo evitiamo i casi particolari di vertici del poligono che
cadono sul lato comune di due pixel, o sul vertice comune di quattro pixel
della griglia.
Materiale di supporto
Qui trovate un esempio di input, un
esempio di output, e un programma grafico che vi consentira' di
visualizzare input e output per controllare la correttezza del risultato.
Algoritmo
1. Dimensionamento della griglia
Dati i valori minimi e massimi delle ascisse e delle ordinate dei
vertici del poligono,
la griglia deve estendersi almeno, su ciascuno dei due assi coordinati,
dalla parte intera inferiore del minimo alla parte intera superiore del
massimo.
2. Determinazione dei pixel da riempire
Ci sono tre tipi di pixel da riempire:
- pixel che contengono un vertice (rossi in figura)
- pixel che sono attraversati da un lato (verdi in figura)
- pixel che sono contenuti interamente all'interno della regione
(gialli in figura)
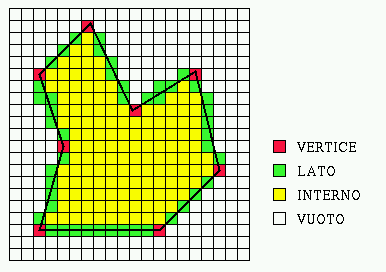
2.1 Ricerca dei pixel contenenti un vertice
Sia V=(x,y) un vertice del poligono.
Il pixel che contiene V si determina semplicemente calcolando la
parte intera inferiore e superiore dei valori di x e
di y.
2.2 Ricerca dei pixel attraversati da un lato
Sia e = V1 - V2 = (x1,y1) - (x2,y2) un lato del poligono.
Siano P1 e P2 i pixel che contengono V1 e
V2.
Gli altri pixel attraversati da e si trovano muovendosi
per adiacenze da P1 a P2.
Per passare da un pixel al successivo, si attraversa il lato
o il vertice che e' intersecato da
e (e che porta d un pixel nuovo, diverso da quello
appena esaminato in precedenza).
2.3 Ricerca dei pixel interni alla regione
Idea di base:
supponiamo di conoscere un pixel P che giace interamente
dentro la regione.
Possiamo muoverci per adiacenze di lati da P
visitando (e riempiendo) tutti i pixel che possiamo raggiungere
senza attraversare pixel appartenenti al contorno della regione.
In pratica si compie una visita in DFS del grafo che ha per nodi
i pixel e ha un arco fra ogni coppia di pixel che condividono un lato.
Questo metodo pero' ha il problema che
bisogna prima trovare un pixel interno P da cui partire.
Variante piu' facile:
Anziche' cercare i pixel da riempire (= quelli interni alla regione),
cerchiamo i pixel da lasciare vuoti (= quelli esterni).
Infatti sappiamo che ogni pixel sul contorno della matrice che
non sia stato marcato come pieno (non contenente vertici ne' attraversato
da lati) e' un pixel esterno alla regione.
Complessita' temporale
Sia p il numero di lati del poligono e sia la nostra griglia
una matrice n X m.
-
Determinare pixel che contengono un vertice costa O(p)
(un numero costante di operazioni per ciascun vertice).
-
Determinare i pixel attraversati da un lato richiede, per ogni lato
e, un numero di operazioni proporzionale al numero di
pixel attraversati da e.
Totale O(p + L) dove L e' il numero totale di
pixel attraversati da lati.
-
Determinare i pixel esterni (e quindi di quelli interni) costa
O(n m) poiche' occorre attribuire uno stato (pieno / vuoto)
a ciascun restante pixel della matrice,
e la visita DFS per adiacenze ha costo lineare.
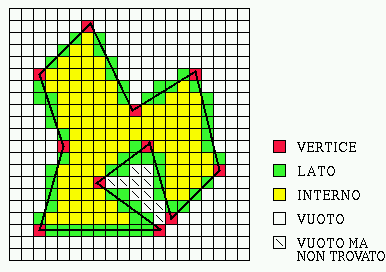
Problemi intrinseci del metodo
Il metodo funziona solo se l'insieme dei pixel esterni e' 4-connesso.
Altrimenti possono restare "sacche" di pixel esterni alla regione
non raggiungibili a partire dal controno della griglia.
Esercizio 2
Scrivere un algoritmo per convertire una regione da una rappresentazione
tramite griglia di pixel ad una rappresentazione tramite quadtree di
regione.
-
INPUT: l'output dell'esercizio 1.
-
OUTPUT: l'elenco delle foglie del quadtree costruito; ogni foglia
e' specificata come:
- le coordinate x0,y0 (due interi) del suo
vertice in basso a sinistra,
- la sua ampiezza w in numero di pixel (un intero positivo),
- e il suo stato: 0 = vuoto, 1 = pieno.
Nota
In questo esercizio non e' richiesto di costruire effettivamente
(memorizzandolo) l'albero quaternario che rappresenta il quadtree, ma
di determinare le sue foglie. Tuttavia non e' vietato, se risulta piu'
semplice, costruire l'albero e poi produrre in output le sue foglie.
Materiale di supporto
Qui trovate un esempio di input, un
esempio di output, e un programma grafico che vi consentira' di
visualizzare l'output per controllare la correttezza del risultato.
Algoritmo
1. Ridimensionamento della griglia
Per poter costruire il quadtree, il numero di pixel su ogni lato
della griglia deve essere una potenza di 2.
Quindi, se la nostra immagine e' m X n pixel,
occorre prima portarla a k X k pixel, dove k e'
la piu' piccola potenza di 2 che sia maggiore di m e
di n, completandola con pixel vuoti.
2. Costruzione del quadtree
E' possibile costruire il quadtree partendo dalla radice
(cioe' iniziando a guardare se per caso l'immagine e' tutta bianca
o tutta nera, in caso contrario dividerla in quattro quadranti e
cosi' ricorsivamente...) oppure partendo dalle foglie
(ossia iniziando a guardare i pixel dell'immagine a 4 a 4 e vedere
se hanno lo stesso colore, nel caso raggrupparli in un quadrato
piu' grande e cosi' via...).
-
Definire un algoritmo atto a questo scopo
-
Valutare quanto costa l'algoritmo definito in funzione del parametro
k = numero di pixel per lato dell'immagine data (dopo averla
completata a potenza di due).


