Dispense di I.U.M. Modellazione Geometrica

Cap.1: Introduzione alla modellazione bidimensionale

Leila De Floriani, Paola Magillo

Modellazione geometrica bidimensionale

Definizione di rappresentazioni per entita' geometriche bidimensionali.

Paradigma della modellazione geometrica

Insieme degli oggetti reali W
Insieme dei modelli matematici M
Insieme delle rappresentazioni R

   +-----+       +-----+       +-----+
   |  W  | ----> |  M  | ----> |  R  |
   +-----+       +-----+       +-----+

Passaggio dal mondo reale W all'astrazione matematica M: fatta dalla mente umana, non formalizzabile.

Passaggio dal modello matematico M alla rappresentazione R usata all'interno dell'elaboratore: formalizzata dallo schema di rappresentazione.

Def. Schema di rappresentazione

Applicazione che associa ad un modello matematico m in M una rappresentazione r in R.

Una rappresentazione e' una stringa finita di simboli appartenenti a un alfabeto.

Modellazione geometrica bidimensionale

Entita' geometriche considerate:

Punto: coppia P = (x,y) di coordinate cartesiane nel piano x-y.
Segmento di curva: definito da
- punti estremi della curva
- equazione della curva
In genere, segmenti di retta (l'equazione segue noti gli estremi)
Regioni piane
Suddivisioni piane (che definiamo in termini di grafi)

Modello matematico di REGIONE PIANA

Una regione piana e' un sottoinsieme del piano che sia:

Chiuso: deve contenere il suo contorno.
Limitato.
Connesso: non deve consistere di piu' parti staccate.
Un insieme e' connesso se ogni coppia di suoi punti puo' essere unita da un segmento di curva (nota: non necessariamente di retta) senza uscire dall'insieme.
Regolare: deve essere uniformemente bidimensionale, avere un suo interno e un suo contorno senza parti "isolate".
Un insieme e' regolare se coincide con la chiusura del suo interno.
Con contorno 1-manifold.
Per ogni punto P appartenente al contorno, esiste sul contorno un intorno di P omeomorfo ad un intervallo aperto.

Una regione piana puo' essere:

Semplicemente connessa: il complementare della regione e' connesso (ogni coppia di punti non appartenenti alla regione puo' essere unita da un segmento di curva senza intersecare la regione).
Molteplicemente connessa: il complementare della regione non e' connesso.

Rappresentazioni di REGIONI PIANE

Dal modello matematico si passa alla rappresentazione.

Le rappresentazioni di regioni piane possono essere suddivise in due categorie:

Rappresentazioni mediante il CONTORNO: descrivono una regione in termini delle curve che la delimitano.
Rappresentazioni basate sullo SPAZIO OCCUPATO (rappresentazioni a pixel): descrivono una regione in base alla porzione di spazio occupata; il piano e' suddiviso in celle elementari di forma quadrata.

Rappresentazioni basate sullo spazio occupato

Tali rappresentazioni sono basate sulla suddivisione di una porzione di piano (che chiameremo immagine) in celle quasi-disgiunte, generalmente di forma quadrata, dette pixel.

+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+

L'immagine e' rappresentata da una griglia di riferimento in cui ciascun elemento e' un pixel.
L'immagine e' l' "universo" di riferimento. Una regione e' descritta nell'ambito di questo universo di riferimento.
Una regione e' rappresentata da un insieme massimale 4-connesso di pixel pieni.

Un pixel dell'immagine e' detto pieno se ha intersezione non vuota con la regione; e' detto vuoto in caso contrario.

+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |XX|XX|XX|  |  |   esempio di rappresentazione
+--+--+--+--+--+--+--+--+   di una regione,
|  |XX|XX|XX|XX|XX|  |  |   in figura XX = pixel pieno
+--+--+--+--+--+--+--+--+
|  |XX|XX|XX|XX|XX|  |  |
+--+--+--+--+--+--+--+--+
|  |  |XX|XX|  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+

Due pixel sono detti 4-adiacenti se sono adiacenti nella direzione orizzontale o verticale (vale a dire se hanno in comune un lato).
```
   +--+
   |  |
+--+--+--+
|  |P |  |     figura: i 4 pixel 4-adiacenti al pixel P
+--+--+--+
   |  |
   +--+
```

Un insieme di pixel in un'immagine e' detto 4-connesso se, per ogni coppia p,q di suoi pixel, esiste una sequenza di pixel p = p0, p1, ..., p(k) = q appartenenti all'insieme e tali che p(i+1) e' 4-adiacente a p(i) per i = 0,1,..., k-1.

   +--+--+                      +--+--+--+
   |  |  |  insieme             |  |  |  |
+--+--+--+  4-connesso          +--+--+--+--+--+
|  |  |  |                               |  |  |
+--+--+--+--+                            +--+--+
|  |  |  |  |                   insieme non 4-connesso
+--+--+--+--+                   (ma e' 8-connesso, ved. dopo)

Una regione e' descritta da un insieme massimale 4-connesso di pixel pieni.

Osservazione

Nella definizione di rappresentazione a pixel, un'immagine del tipo

+--+--+--+--+--+--+--+--+
|  |  |  |XX|XX|XX|  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |XX|XX|XX|  |  |
+--+--+--+--+--+--+--+--+
|  |XX|XX|  |  |  |XX|  |
+--+--+--+--+--+--+--+--+
|  |XX|XX|  |  |  |XX|  |
+--+--+--+--+--+--+--+--+
|  |  |XX|  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+

rappresenta un insieme di tre regioni.

Versione alternativa

Due pixel sono detti 8-adiacenti se sono adiacenti lungo una direzione orizzontale, verticale o diagonale (cioe' se hanno in comune almeno un vertice: un vertice o uno spigolo).
```
+--+--+          +--+
|  |  |          |  |
+--+--+          +--+--+ 
                    |  | vertice
spigolo             +--+
```
Un insieme di pixel in un'immagine e' detto 8-connesso se, per ogni coppia p,q di suoi pixel, esiste una sequenza di pixel p = p0, p1, ..., p(k) = q appartenenti all'insieme e tali che p(i+1) e' 8-adiacente a p(i) per i = 0,1,..., k-1.

Una regione e' descritta da un insieme R massimale 4-connesso di pixel pieni, tale che

per ogni coppia di pixel tra loro 8-adiacenti ma non 4-adiacenti appartenenti a R, esiste un pixel appartenente a R e 4-adiacente a entrambi.

                        +--+--+      +--+--+
                        |XX|  |      |  |XX|
configurazioni vietate: +--+--+      +--+--+
                        |  |XX|      |XX|  |
                        +--+--+      +--+--+

                        +--+--+      +--+--+
                        |XX|XX|      |XX|XX|
configurazioni ammesse: +--+--+      +--+--+    ecc.
                        |  |XX|      |XX|  |
                        +--+--+      +--+--+

non esiste un sottoinsieme S 8-connesso dell'immagine formato da pixel pieni per cui R sia contenuto in S ma non uguale a S.

Dalla condizione 1 segue che configurazioni di questo tipo non sono rappresentazioni valide di regioni:

+--+--+--+--+--+--+--+--+
|  |  |  |XX|XX|XX|  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |XX|XX|XX|  |  |   infatti il contorno
+--+--+--+--+--+--+--+--+   non sarebbe 
|  |XX|XX|  |  |XX|  |  |   1-manifold
+--+--+--+--+--+--+--+--+
|  |XX|XX|  |  |XX|  |  |
+--+--+--+--+--+--+--+--+
|  |  |XX|XX|XX|XX|  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+

Dalla condizione 2 segue che i pixel appartenenti a due regioni distinte non sono mai 8-connessi.

Strutture dati

Una rappresenazione a pixel fornisce una descrizione approssimata di una regione piana.

La risoluzione e' determinata dalla dimensione del pixel. La descrizione e' tanto piu' accurata quanto piu' fine e' la suddivisione dell'immagine in pixel.

Strutture dati per la codifica di una rappresentazione a pixel: matrice bidimensionale binaria:

Pixel pieno (black) = 1
Pixel vuoto (white) = 0

Se l'immagine e' costituita da k x k pixel, la dimensione della matrice e' k x k.

Proprieta' delle rappresentazioni a pixel

Forniscono una descrizione approssimata di una regione.
Al crescere della risoluzione, aumenta la dimensione della rappresentazione (con considerevole occupazione di memoria)
Rappresentazione adatta alla visualizzazione

Calcolo di operazioni booleane (intersezione, unione, differenza di regioni) concettualmente semplice.

Esempio: unione = fare AND pixel a pixel delle matrici che rappresentano le due regioni

+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+ 
|  |  |  |  |  |  |  |  |      |  |  |  |2 |2 |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |1 |1 |1 |1 |  |  |  |      |  |  |  |2 |2 |2 |2 |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |  |  |  |      |  |  |  |2 |2 |2 |2 |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |1 |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |  |  |1 |1 |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
immagine regione R1            immagine regione R2
(pixel pieni marcati 1)        (pixel pieni marcati 2)

+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+ 
|  |  |  |2 |2 |  |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |1 |1 |12|12|2 |2 |  |      |  |  |  |12|12|  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |1 |12|12|2 |2 |  |      |  |  |  |12|12|  |  |  |
+--+--+--+--+--+--+--+--+  =   +--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |1 |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |  |  |1 |1 |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |      |  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+      +--+--+--+--+--+--+--+--+
immagine intersezione di R1 ed R2 (pixel pieni marcati 12)

Rappresentazioni a pixel adattive: QUADREE di regione

Il termine quadtree indica una classe di rappresentazioni gerarchiche di entita' geometriche (punti, segmenti, regioni, superfici, solidi) basate sul principio di scomposizione ricorsiva e regolare dello spazio.

Tali rappresentazioni sono classificate in base alle entita' geometriche che descrivono.

Noi ora ci occupiamo del Quadtree di regione (region quadtree).

E' basato sulla suddivisione ricorsiva di un'immagine in quadranti: nord-ovest (NW), nord-est (NE), sud-ovest (SW), sud-est (SE), della stessa dimensione.
Il processo termina quando si giunge a blocchi contenenti solo pixel vuoti o solo pixel pieni (questi ultimi appartengono alla regione).

Un quadtree e' descritto da un albero quaternario in cui:

La radice corrisponde all'intera immagine.
I nodi terminali (foglie) corrispondono a blocchi omogenei di pixel.
Nodo terminale pieno (black): il blocco corrispondente e' formato interamente da pixel pieni.
Nodo terminale vuoto (white): il blocco corrispondente e' formato interamente da pixel vuoti.
I nodi interni corrispondono a blocchi parzialmente pieni e parzialmente vuoti. Detti anche nodi neutri (grey).

+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+
|  |  |  |  |  |  |  |  |
+--+--+--+--+--+--+--+--+  matrice binaria 0/1 che
|  |  |  |  |1 |1 |1 |1 |  rappresenta una regione
+--+--+--+--+--+--+--+--+  (per leggibilita' sono
|  |  |  |  |1 |1 |1 |1 |  marcati solo gli "1")
+--+--+--+--+--+--+--+--+
|  |  |  |1 |1 |1 |1 |1 |
+--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |1 |1 |1 |
+--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |1 |  |  |
+--+--+--+--+--+--+--+--+
|  |  |1 |1 |1 |  |  |  |
+--+--+--+--+--+--+--+--+

+--+--+--+--+--+--+--+--+
|           |     |     |
+           + F0  + G0  +
|           |     |     |
+     B0    +--+--+--+--+  divisione in blocchi del
|           |     |     |  relativo quadtree
+           + H1  + I1  +  (i blocchi con etichetta
|           |     |     |  terminante per "1" sono
+--+--+--+--+--+--+--+--+  pieni)
|     |R0|S1|     |     |
+ J0  +--+--+ N1  + O1  +
|     |T1|U1|     |     |
+--+--+--+--+--+--+--+--+
|     |     |V1|W1|     |  
+ L0  + M1  +--+--+ Q0  +
|     |     |X1|Y0|     |
+--+--+--+--+--+--+--+--+

l'albero quaternario

                          A
                          |
 +----------+-------------+-------------+
 |(NW)      |(NE)         |(SW)         |(SE)
B0          C             D             E
            |             |             |
      +--+--+--+    +--+--+--+    +--+--+--+
      |  |  |  |    |  |  |  |    |  |  |  |
     F0 G0 H1 I1   J0  K  L0 M1  N1 01  P  Q0
                       |                |
                 +--+--+--+       +--+--+--+
                 |  |  |  |       |  |  |  |
                R0 S1  T1 U1     V1 W1  X1 Y0

Proprieta' del quadtree di regione

Fornisce una descrizione approssimata (precisione determinata dalla dimensione del pixel).
Semplicita' ed efficienza delle operazioni booleane.
Rappresentazione piu' compatta rispetto alla rappresentazione non gerarchica.

Rappresentazioni mediante il contorno

Consideriamo regioni piane poligonali, cioe' regioni contornate da poligoni (semplici).

Definizioni

Un poligono e' definito da un insieme finito di segmenti nel piano, in cui ogni estremo di segmento e' comune a esattamente due segmenti.

I segmenti sono detti lati del poligono.
Gli estremi dei segmenti sono detti vertici del poligono.

Un poligono e' detto semplice se non esiste alcuna coppia di lati intersecantisi (al di fuori degli estremi).

Teorema di Jordan

Un poligono semplice (in generale, una curva semplice e chiusa) partiziona il piano in due regioni distinte: interno ed esterno.

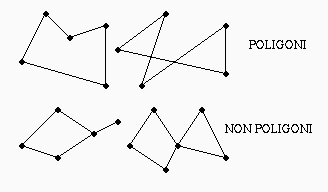
Un poligono e' detto convesso se il suo interno e' un insieme convesso.

Un insieme S di punti nel piano euclideo e' convesso se e solo se, per ogni coppia di punti in S il segmento di retta che li unisce e' interno ad S.

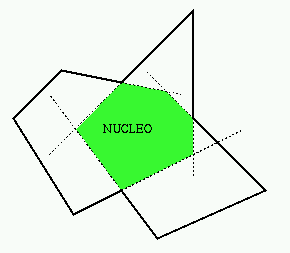
Un poligono semplice e' detto a forma di stella (o stellato) se esiste un punto Q non esterno al poligono (vale a dire che Q puo' appartenere al poligono o al suo interno) tale che, per ogni punto P del poligono, il segmento di retta PQ e' interno al poligono.

Il luogo dei punti che godono della proprieta' precedente e' detto nucleo (o kernel) del poligono a stella.

Nota: un poligono convesso e' anche un poligono a stella, e il suo nucleo concide con il poligono + il suo interno.

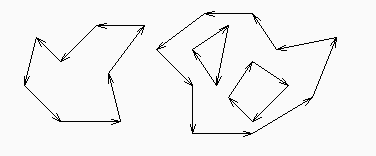
Rappresentazioni per regioni piane poligonali

Una regione poligonale semplicemente connessa e' descritta da un poligono semplice.

Una regione poligonale molteplicemente connessa e' descritta da un insieme di poligoni semplici. Viene anche detta, impropriamente, poligono con buchi. L'insieme di poligoni e' dato in una lista dove per convenzione il primo poligono rappresenta il contorno esterno.

Rappresentazione di un poligono

Un poligono e' descritto da una sequenza ordinata di vertici (struttura a lista): Pigreco = [P1,P2,...,P(n)]

Se il poligono e' semplice, il lato P(i)P(i+1) e' orientato in modo tale che l'interno del poligono giace alla sinistra della retta orientata da P(i) a P(i+1). Vale a dire: il poligono e' ordinato in senso antiorario.

Quando un poligono semplice e' usato all'interno della rappresentazione di una regione poligonale, le convenzioni sono un po' diverse:

Regione semplicemente connessa (contornata da un solo poligono semplice): il poligono e' ordinato in senso antiorario.
Regione molteplicemente connessa (contornata da piu' poligoni semplici): il primo poligono (contorno esterno) e' ordinato in senso antiorario, gli altri (contorni interni) in senso orario.

Regola base: la regione sta sempre a sinistra del suo contorno orientato.