p punto di intersezione di due segmenti s1
ed s2 (con s1 sopra s2 all'immediata
sinistra di p):
- sia s3 il segmento sopra s1
- sia s4 il segmento sotto s2
- test intersezione (s2,s3)
- test intersezione (s1,s4)
- scambia s1 ed s2 in L
Descrizione dell'algoritmo
Input:
lista S dei segmenti, ciascuno definito dalle coordinate
dei suoi due estremi.
Algorithm LINE_SEGMENT_INTERSECTION
begin
inizializza E con gli estremi dei segmenti di S;
p := FIRST(E);
(* p e' l'evento corrente *)
repeat
case event_type(p)
estremo sinistro:
begin
s := segmento di cui p e' estremo sinistro;
INSERT_SLS(s,L);
s1 := ABOVE(s,L);
s2 := BELOW(s,L);
if (s1 interseca s) then UPDATE(s,s1,E);
if (s2 interseca s) then UPDATE(s,s2,E);
end
estremo destro:
begin
s := segmento di cui p e' estremo destro;
s1 := ABOVE(s,L);
s2 := BELOW(s,L);
if (s1 interseca s2 alla destra di p) then UPDATE(s1,s2,E);
DELETE(s,L);
end
punto di intersezione:
begin
(s1,s2) := segmenti di cui p e' intersezione;
(* con s1 = ABOVE(s2) alla sinistra di p *)
s3 := ABOVE(s1,L);
s4 := BELOW(s2,L);
if (s3 interseca s2 alla destra di p) then UPDATE(s3,s2,E);
if (s1 interseca s4 alla destra di p) then UPDATE(s1,s4,E);
scambia s1 ed s2 in L;
end
end case
p := NEXT(E,p);
until P = LAST(E)
end algorithm
Procedure UPDATE(s,s',E)
begin
p := evento punto di intersezione definito da s ed s';
if not MEMBER(p,E)
begin
INSERT_SLS(p,E);
(x,y) := coordinate dell'intersezione;
output (s,s',(x,y));
end
end
Correttezza dell'algoritmo
L'algoritmo trova tutte le intersezioni, in quanto:
- solo segmenti consecutivi possono intersecarsi
- tutte le coppie di segmenti consecutivi sono esaminate correttamente
almeno una volta
Nessuna intersezione e' stampata piu' di una volta
(segue da come e' fatta la procedura UPDATE).
Complessita' temporale
Inizializzazione di E: O(N log N)
per ordinamento di 2N informazioni e per inserimento in E.
Elaborazione di un evento: O(log N) poiche':
- intersezione di due segmenti: O(1)
- INSERT_SLS: O(log N) in quanto O(N)
informazioni in L
- ABOVE, BELOW: O(log N)
- procedura UPDATE = MEMBER + INSERT:
E puo' contenere al piu' 2N+K informazioni
dove K = numero di intersezioni degli N segmenti.
Poiche' K <= N su 2 = O(N^2),
MEMBER + INSERT hanno costo in O(log(2N+K)) = O(log N)
Calcolo di NEXT: O(log(2N+K)) = O(log N)
Ciclo repeat: ripetuto 2N+K volte.
Complessita' totale (nel caso peggiore): O((N+K)log N).
Tale complessita' dipende dalla dimensione dell'output
Note
Lower bound per il problema del calcolo dell'intersezione di N
segmenti e' Omega(K + N log N)
Algoritmo ottimale in Theta(K + N log N) sviluppato da Chazelle e
Edelsbrunner (1998).
Test di intersezione di segmenti (Problema P2)
Idea di base
Poiche' si vuole stabilire solo se esiste un'intersezione, e' inutile
calcolare tutte le K intersezioni.
Supponiamo di utilizzare come eventi solo i 2N estremi
dei segmenti dati.
Siamo in grado di trovare un'intersezione quando esiste?
Algoritmo
-
ordinare da sinistra a destra gli estremi dei segmenti
-
per ogni evento p in E:
-
se p estremo sinistro di segmento s:
-
inserisci s in L
-
test di intersezione di s con i due segmenti rispettivamente
al di sotto e al di sopra di s
-
se p estremo destro di segmento s:
-
test di intersezione fra i due segmenti al di sotto e al di sopra di
s
-
elimina s da L
-
non appena si determina l'esistenza di un'intersezione,
l'algoritmo termina con risposta SI
-
se si esauriscono i 2N eventi senza trovare intersezioni,
l'algoritmo termina con risposta NO
Correttezza dell'algoritmo
L'algoritmo trova sempre un'intersezione in quanto
la struttura dati contiene una rappresentazione corretta della relazione di
precedenza alla sinistra del punto di intersezione piu' a sinistra.
NOTA:
l'intersezione piu' a sinistra non e' detto che sia la prima intersezione
trovata.
Strutture dati
Per event-point schedule si puo' utilizzare una struttura statica, come ad
esempio un array di 2N elementi, in quanto tutti gli eventi sono
noti a priori.
Per lo sweep-line status si usa la stessa struttura vista nell'algoritmo
di calcolo pelle intersezioni.
Schema dell'algoritmo
L'ordinamento preliminare degli estremi dei segmenti dati avviene nello
stesso modo visto per l'algoritmo di calcolo delle intersezioni
(algoritmo per problema P1):
- punti di ascissa minore precedono punti di ascissa maggiore
- a parita' di ascissa, punti di ordinata minore precedono punti di
ordinata maggiore
- a partita' di entrambe le coordinate, estremi destri precedono
estremi sinistri
Algorithm LINE_INTERSECTION_TEST
begin
ordina i 2N punti estremi dei segmenti; (* come spiegato sopra *)
inserisci tali punti ordinati in array E[1..2N];
for i=1 to 2N do
p := E[i]; (* p e' l'evento corrente *)
s := segmento di cui p e' estremo;
if p estremo sinistro
begin
INSERT_SLS(s,L);
s1 := ABOVE(s,L);
s2 := BELOW(s,L);
if (s1 interseca s) then return SI
if (s2 interseca s) then return SI
end
else (* p estremo destro *)
begin
s1 := ABOVE(s,L);
s2 := BELOW(s,L);
if (s1 interseca s2) then return SI
DELETE(s,L);
end
end for
end algorithm
Complessita' temporale
Inizializzazione di E: O(N log N) per l'ordinamento.
Operazioni su un singolo evento: O(log N).
Ciclo for ripetuto 2N volte.
Complessita' totale: O(N log N)
Si puo' dimostrare che l'algoritmo e' ottimale nel caso peggiore.
Conseguenze
Test di intersezione di due poligoni semplici
con O(N) lati = O(N log N).
Test per stabilire se una sequenza di N segmenti definisce
un poligono semplice = O(N log N).
Intersezione di poligoni
Problema P1: calcolo dell'intersezione di poligoni semplici
Dati due poligoni semplici P e Q,
determinatre l'intersezione di P e Q.
Problema P2: test di intersezione fra poligoni semplici
Dati due poligoni semplici P e Q, determinare se P
e Q si intersecano.
- Consideriamo problema P1 per poligoni convessi.
- Consideriamo problema P2 nel caso generale di poligoni semplici.
Calcolo dell'intersezione di poligoni convessi
Problema
Dati due poligoni convessi P (con L vertici) e
Q (con M vertici), calcolare il poligono intersezione.
Teorema
L'intersezione di un poligono convesso P con L lati con un
poligono convesso Q con M lati (se non vuota o degenere)
e' un poligono convesso con al piu' L+M lati.
Dimostrazione
Basta osservare che l'intersezione delle due regioni poligonali convesse
definite dai due poligoni P e Q dati e' l'intersezione
degli L+M semipiani definiti dalle rette orientate associate ai
lati di P e Q.
Nota: per retta associata ad un lato di P (o di Q)
consideriamo, tra i due semipiani definiti da essa, quello contenente
P (o Q).

Osservazioni
-
Un lato di P puo' avere 0,1 o 2 intersezioni con Q (e
viceversa).
-
Il contorno del poligono intersezione consiste di catene alternate di vertici
dei due poligoni; l'alternanza delle catene avviene ai punti di intersezione.
Metodo delle strisce
[Shamos e Hoey, 1976; ved. anche Preparata e Shamos, cap. 7.2]
Idea
Ridurre il problema dell'intersezione di sue poligoni convessi al problema
dell'intersezione di L+M regioni di forma geometrica semplice
(trapezoidi).

Procedimento
-
Costruire strisce (ad esempio verticali) considerando le rette verticali
passanti per i vertici dei due poligoni.
Abbiamo al piu' L+M rette verticali, quindi al piu'
L+M-1 strisce.
-
Calcolare le intersezioni delle due regioni poligonali definite da
P e da Q all'interno di ciascuna striscia.
Si noti che ciascuna retta ha al piu' due intersezioni con ciascuno
dei due poligoni, pertanto l'intersezione di una striscia con un poligono
convesso e' un trapezoide.
Quindi in ciascuna striscia si deve effettuare l'intersezione di due
trapezoidi.
-
Fondere assieme le varie intersezioni risultati lungo i segmenti verticali.
Questo portera' alla regione poligonale convessa che definisce l'intersezione
di P e Q.
Passo 1: costruzione delle strisce verticali
Ordinare in una singola sequenza i vertici dei due poligoni P
e Q.
Supponendo che ciascuno fra P e Q sia fornito come
sequenza in senso antiorario dei suoi vertici, l'ordinamento si puo'
effettuare in tempo lineare nel modo seguente:
-
Si determinano il vertice Pmin di ascissa minima ed il vertice
Pmax di ascissa massima del poligono P.
Tempo: O(L).
-
Si spezza la catena di vertici di P in due:
-
quella dei vertici da Pmin a Pmax
-
quella dei vertici dal successivo di Pmax al precedente
di Pmin
La prima catena e' lasciata nell'orientamento dato, la seconda viene
rivoltata, ottenendo cosi' due liste di punti entrambe ordinate per
ascissa non decrescente.
Si immergono ordinatamente le due catene.
Tempo: O(L).
-
Si effettua la stessa operazione per il poligono Q.
Tempo: O(M).
-
Si immergono le due liste ordinate di vertici cosi' ottenute da P
e da Q. Tempo: O(L+M).
In figura:
per P le due catene sono [P1,P2,P4,P4] e [P6,P5],
la catena ordinata complessiva e' [P1,P2,P6,P5,P3,P4].

Passo 2: calcolo dell'intersezione in ogni striscia
Puo' essere effettuata mediante una tecnica di plane-sweep considerando
le strisce da sinistra a destra.
Per ogni striscia s si calcola (se esiste) l'intersezione
P(s) di P e l'intersezione Q(s) di Q
con s.
P(s) e Q(s) sono entrambi trapezoidi con due lati
verticali giacenti su rette prefissate.
L'intersezione di due trapezoidi cosi' fatti e' un poligono con al
piu' 6 lati.
Passo 2: immersione dei risultati parziali
Per ciascuna striscia s, si unisce l'intersezione trovata nella
striscia s con l'intersezione trovata nella striscia precedente.
L'unione delle intersezioni in due strisce consecutive avviene mediante
l'eliminazione del lato verticale comune alle due intersezioni.
Complessita'
L'intersezione del poligono P (o Q) con una striscia
a richiede tempo O(1) purche' sia possibile in tempo costante,
dato un vertice V di
P (o di Q) accedere ai due lati che hanno
in comune il vertice V.
L'intersezione dei due trapezoidi all'interno di ogni striscia e' effettuata
in O(1), e cosi' l'immersione di due intersezioni consecutive.
L'algoritmo ha complessita' Theta(L+M).
Note
-
Un algoritmo analogo puo' essere applicato per il calcolo dell'unione
o della differenza di poligoni convessi
(ma il risultato sara' un poligono semplice o una collezione di
poligoni semplici).
-
Lo stesso procedimento puo' essere applicato per risolvere il problema
del test di intersezione (problema P2) fra poligoni convessi,
sempre in Theta(L+M).
Intersezione di due poligoni semplici (cenno)
Consideriamo il problema P1: Determinare l'intersezione di due poligoni
semplici.
Osservazioni:
-
L'intersezione di due poligoni semplici (non convessi) e' formata da
uno o piu' poligoni
-
L'intersezione di due poligoni semplici (non convessi) con L ed
M lati puo' avere O(LM) lati.
Esempio di intersezione formata da O(L+M) poligoni e lati:
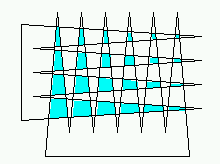
Le due osservazioni valgono anche se i due poligoni sono poligoni a stella.
Teorema
Determinare l'intersezione di due poligoni semplici (anche a stella)
ciascuno con N lati ha una complessita' Omega(N^2) nel
caso peggiore.
Da questo risultato segue che:
-
algoritmi per il calcolo di intersezione hanno complessita' almeno
quadratica
-
il problema del calcolo delle superfici nascoste per poligoni qualunque
ha complessita' almeno quadratica
Il problema P1 per poligoni semplici si riduce al problema di calcolare
le intersezioni di N segmenti nel piano.
Test di intersezione per poligoni semplici
Due poligoni semplici P e Q si intersecano se e solo
se vale una delle tre condizioni:
- P e' contenuto in Q
- Q e' contenuto in P
- esiste intersezione fra un lato di P e un lato di Q
Algorimo
-
Stabilire se esiste intersezione di lati; in caso affermativo l'algorimo
termina con risposta SI; altrimenti va al passo 2.
-
Stabilire se P e' contenuto in Q o se Q
e' contenuto in P; in caso affermativo l'algorimo termina
con risposta SI; altrimenti termina con risposta NO.
Passo 1
E' riducibile al problema del test di intersezione fra N=L+M
segmenti nel piano.
La complessita' e' O(N log N) = O((L+M) log (L+M)).
Passo 2
Per stabilire se P e' contenuto in Q basta stabilire
se un qualunque vertice di P e' contenuto in Q (questo
e' vero poiche' sappiamo che i lati di P e di Q non si
intersecano).
Complessita': O(M).
Per stabilire se Q e' contenuto in P si opera in modo
analogo. Complessita': O(L).
Complessita' del passo 2: O(L+M).
Complessita' totale dell'algoritmo (passi 1+2): O((L+M) log (L+M)).
Ottimizzazione
Puo' essere bene effettuare un test preliminare sui rettangoli minimali
R(P) ed R(Q) che contengono i due poligoni
P e Q rispettivamente.
Se R(P) ed R(Q) hanno intersezione nulla,
possiamo concludere che P e Q non si intersecano.
In caso contrario dobbiamo procedere applicando l'algoritmo
di test d'intersezione descritto sopra.
Il rettangolo minimale R(P) e' definito come il piu' piccolo
rettangolo con lati paralleli agli assi cartesiani contenente P.
R(P) sara' il rettangolo di diagonale
(x_min,y_min)-(x_max,y_max)
dove x_min, x_max rappresentano il valore minimo e
massimo dell'ascissa dei vertici di P,
e y_min, y_max rappresentano il valore minimo e
massimo dell'ordinata dei vertici di P.
Test di "semplicita" di un poligono
E' un altro esempio di problema riducibile al problema del test di
intersezione di segmenti.
Problema:
Data una lista di punti distinti,
tale lista definisce un poligono semplice?
Un poligono e' semplice se e solo se nessuna coppia di lati si interseca
(eccetto che nei vertici estremi).
Soluzione:
E' sufficiente stabilire nell'insieme di segmenti
ottenuto unendo ciascun punto della lista al punto seguente (e l'ultimo
al primo) vi sono intersezioni.
Complessita' nel caso peggiore: O(N log N).










