I.U.M. Modellazione Geometrica

Corso di I.U.M. Modellazione Geometrica

PARTE PRATICA 1

Consideriamo tre problemi geometrici:

1. Orientamento di una terna di punti
2. Determinazione se un punto e' interno / esterno / sul contorno di un poligono convesso (in particolare di un triangolo)
3. Calcolo della quota di un punto su un terreno modellato a triangoli

Orientamento di una terna di punti

Una delle primitive geometriche forndamentali, usata come operazione primitiva in un problemi piu' complessi.

Dati tre punti A, B, C, da che parte giace C rispetto alla retta passante per A, B ed orientata da A verso B?

Risposte possibili:

C giace a destra di AB (la terna ABC definisce una svolta in senso orario),
C giace a sinistra di AB (la terna ABC definisce una svolta in senso antiorario),
C e' allineato con AB.

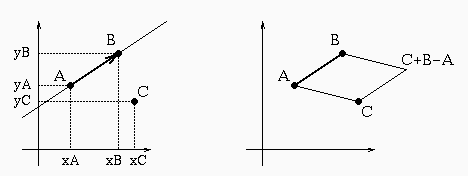
Vari modi di vedere il problema, portano tutti allo stesso algoritmo:

Modo 1. Prendere le coordinate di C, sostituirle nell'equazione della retta orientata AB, e vedere che segno ha il risultato.
Modo 2. Calcolare l'area con segno del parallelogramma di vertici B, A, C, (C+B-A) e vedere che segno ha.

Algoritmo 1 (con equazione della retta)

Equazione della retta orientata AB:
(x-xA)/(xB-xA) = (y-yA)/(yB-yA)
(x-xA)(yB-yA) - (y-yA)(xB-xA) = 0

Polinomio che si ottiene sostituendo le coordinate di C:
(xC-xA)(yB-yA) - (yC-yA)(xB-xA)

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Algoritmo 2 (con area del parallelogramma)

Si considerano i punti A=(xA,yA), B=(xB,yB), C=(xC,yC), D=C+B-A=(xD,yD)=(xC+xB-xA,yC+yB-yA), E=(xA,yD), F=(xD,yA).

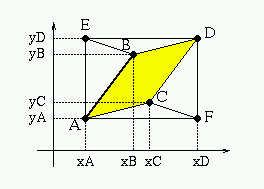
Area del parallelogramma ABDC = area del rettangolo AEDF - aree dei triangoli EAB, EBD, AFC, CFD (tutte aree con segno).

Area(AEDF) = (xD-xA)*(yD-yA) = (xC+xB-2xA)*(yC+yB-2yA).
Area(EAB) = Area(CFD) = 0.5*(xD-xC)*(yD-yA) = 0.5*(xB-xA)*(yC+yB-2yA).
Area(EBD) = Area(AFC) = 0.5*(xD-xA)*(yD-yC) = 0.5*(xC+xB-2xA)*(yB-yA).

Area(ABDC) = Area(AEDF) - 2*Area(EAB) - 2*Area(EBD) =
(xC+xB-2xA)*(yC+yB-2yA) - (xB-xA)*(yC+yB-2yA) - (xC+xB-2xA)*(yB-yA) = ...
... = (xC-xA)*(yB-yA) - (xB-xA)*(yC-yA).

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Conclusione

L'espressione di cui si valuta il segno e' il determinante

| yB-yA  yC-yA |
| xB-xA  xC-xA |

= (yB-yA)(xC-xA) - (yC-yA)(xB-xA)
= yA*xB - yB*xA + yC*xA - yA*xC + yB*xC - yC*xB

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Problemi numerici

Se il risultato e' molto piccolo in valore assoluto, puo' succedere che gli sia attribuito un segno errato a causa di errori di approssimazione inevitabili usando l'aritmetica floating point.

Una soluzione che di solito funziona e' quella di assumere una tolleranza epsilon>0 (molto piccola) e considerare come uguali a zero tutte le quantita' che in valore assoluto sono minori di epsilon.

In pratica si risponde che C e' allineato con A e B se la sua distanza dalla retta e' molto piccola, ovvero se l'area del parallelogramma e' molto piccola.

Complessita' temporale

Costante in quanto e' coinvolto un numero fissato di punti e di coordinate (3 e 6 rispettivamente).

Determinazione della posizione di un punto rispetto ad un poligono convesso

Siano P1, P2, P3, ..., P(n) i vertici di un poligono convesso, ordinati in senso antiorario.
Sia Q un altro punto. Qsta dentro, fuori, o sul contorno del poligono?

Q giace dentro il poligono se Q giace a sinistra di tutte le rette orientate passanti per lati del poligono (la retta orientata da P(i) a P(i+1), per ogni i da 1 a n).
Q giace fuori dal poligono se Q giace a destra di almeno una delle rette orientate sopra dette.
Q giace sul contorno del poligono se Q e' allineato con almeno una delle rette sopra dette, e giace a sinistra delle rimanenti. In particolare:
- se Q e' allineato con una e a sinistra delle altre, allora Q giace all'interno di un lato
- se Q e' allineato con due e a sinistra delle altre, Q coincide con un vertice
- non sono possibili altri casi.

Complessita' temporale

O(n) dove n e' il numero di vertici (o, equivalentemente, di lati) del poligono.

Nel caso peggione (punto interno o sul contorno), si riduce ad esattamente n chiamate alla primitiva che controlla l'orientamento di una terna di punti. Ciascuna chiamata ha un costo costante.

Nel caso particolare in cui il poligono e' un triangolo (n=3), la complessita' e' O(n) = O(3) = O(1) cioe' costante.

Calcolo della quota di un punto su un terreno modellato a triangoli

Matematicamente, un terreno e' una superficie nello spazio 3D che puo' essere proiettata ortogonalmente sul piano xy senza che due punti della superficie vadano a coincidere sullo stesso punto del piano.

La regione piana che si ottiene dalla proiezione sul piano xy e' chiamata dominio del terreno. La superficie del terreno puo' essere pensata come il grafico di una funzione definita sui punti del dominio, che associa ad ogni punto (x,y) del dominio la relativa quota z sul terreno.

In un terreno reale, questa funzione non ha espressione matematica, quindi non e' rappresentabile finitamente. Approssimiamo il terreno reale discretizzando la funzione. Come si approssima la linea curva di un grafico 2D mediante una catena di segmenti, cosi' noi approssimiamo la superficie del terreno mediante un reticolo di facce triangolari.

Il dominio e' suddiviso in triangoli. Di ogni triangolo sono note le quote dei tre vertici, che mappano il triangolo stesso in 3D. L'insieme di tutti i triangoli fornisce l'approssimazione a facce piane dell'intero terreno.

Inconsistenze potrebbero sorgere se triangoli confinanti in 2D fossero mappati in 3D a quote diverse. In tal caso l'insieme di facce in 3D non sarebbe piu' il grafico di una funzione, l'effetto evidente sarebbe la presenza di "spaccature" nella superficie. Per evitare questo, e' necessario che la suddivisione del domimio in triangoli soddisfi certe proprieta'. Tali proprieta' rispecchiano il concetto di suddivisione piana, introdotto piu' avanti nel corso.
Per adesso supponiamo semplicemente di avere in input un insieme di triangoli "buoni".

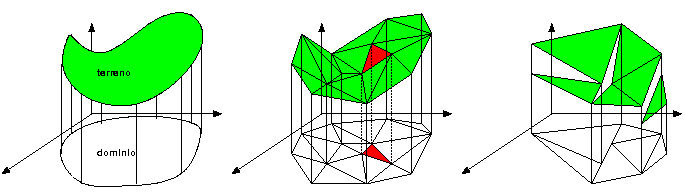
Figura: terreno e suo dominio, terreno discretizzato in triangoli, configurazione di triangoli non "buona" per rappresentare un terreno.

Definizione del problema

Dato un insieme di triangoli descriventi un terreno ed un punto P=(xP,yP) nel piano, determinare la quota corrispondente a P sul terreno.

Algoritmo

Si esaminano uno per uno i triangoli
Per ciascun triangolo t esaminato, si controlla se il punto P cade all'interno o sul contorno di t (considerando punto e triangolo in 2D sul piano xy)
Non appena si trova un triangolo t tale che P cade all'interno o sul contorno di t, si calcola la quota di P su tale triangolo (considerando il triangolo in 3D); l'algoritmo termina
Se si sono esaminati tutti i triangoli senza trovarne uno che contenga P al suo interno o sul suo contorno, allora significa che il punto P e' esterno al dominio; l'algoritmo termina

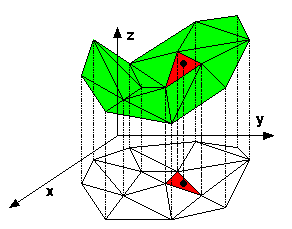
Se il punto P giace sul contorno comune di piu' triangoli, l'algoritmo sopra descritto calcola la quota di P in base ad uno dei triangoli in questione (il primo che incontra). Questo e' corretto perche' triangoli confinanti in 2D assumono in 3D la stessa quota sul confine comune (in quanto abbiamo assunto che l'insieme di triangoli sia "buono").

Calcolo della quota

Siano P1=(x1,y1), P2=(x2,y2), P3=(x3,y3) i tre vertici del triangolo in cuo cade il punto P, e siano z1, z2, z3 le quote corrispondenti.

L'equazione del piano passante per i tre vertici mappati in 3D e' la seguente:

(x-x1)a + (y-y1)b + (z-z1)c = 0

dove

a = (y1-y2)(z1-z3)-(z1-z2)(y1-y3)
b = (z1-z2)(x1-x3)-(x1-x2)(z1-z3)
c = (x1-x2)(y1-y3)-(y1-y2)(x1-x3)

in cui bisogna sostituire le due coordinate (xP,yP) di P e ricavare la z:

z = ( -((xP-x1)a + (yP-y1)b) / c ) + z1

Il denominatore c e' garantito diverso da zero se il triangolo non e' degenere in 2D. Infatti si annullerebbe solo se P3 fosse collineare a P1 e P2.

Files

monte.raw - un esempio di insieme di triangoli in input
visraw.c - il programma visualizzatore con cui potete controllare la correttezza del vostro programma (visualizza il terreno e il punto con la quota che avete calcolato, se il punto giace sul terreno allora e' giusto)
readme1.txt - istruzioni per la compilazione e l'uso del visualizzatore
makefile - per compilare il programma visualizzatore

Il visualizzatore usa le librerie grafiche OpenGL (versione MesaGL) e Glut, installate nel laboratorio SW2.

Il formato del file che contiene i triangoli e' i seguente:

il numero di triangoli (1 intero)
per ogni triangolo, le coordinate dei tre vertici nell'ordine x1 y1 z1 x2 y2 z2 x3 y3 z3 (in totale 9 float per triangolo)

I separatori possono essere spazi, tabulazioni, ritorni a capo in numero arbitrario e anche mischiati fra loro.
Suggerimento: per la lettura del file di triangoli guardate come e' fatta la funzione di lettura in visraw.c.