NOTE AL PRIMO ESERCIZIO DI LABORATORIO

Consideriamo tre problemi geometrici:

1. Orientamento di una terna di punti
2. Determinazione se un punto e' interno / esterno / sul contorno di un triangolo
3. Costruzione di una triangolazione di un poligono semplice

Algoritmo per problema 2 usa 1 come operazione ausiliaria. Algoritmo per problema 3 usa 1 e 2 come operazioni ausiliarie.

Che cosa vi diamo:

codice per 1 e 2
parte del codice per 3 da completare

Maggiori dettagli su che cosa dovete fare in fondo.

Orientamento di una terna di punti

Una delle primitive geometriche forndamentali, usata come operazione primitiva in un problemi piu' complessi.

Dati tre punti A, B, C, da che parte sta C rispetto alla retta passante per A, B ed orientata da A verso B ?

Risposte possibili:

C giace a destra di AB (la terna ABC svolta in senso orario),
C giace a sinistra di AB (la terna ABC svolta in senso antiorario),
C e' allineato con AB.

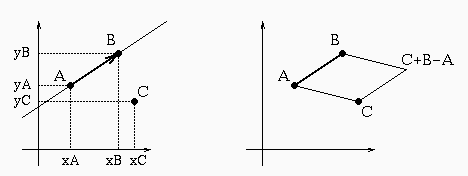
Vari modi di vedere il problema, portano tutti allo stesso algoritmo:

Modo 1. Prendo le coordinate di C, le sostituisco nell'equazione della retta per A, B, e vedo che segno ha il risultato.
Modo 2. Calcolo l'area con segno del parallelogramma di vertici B, A, C, (C+B-A) e vedo che segno ha.

Algoritmo 1 (con equazione della retta)

Equazione della retta per A, B:
(x-xA)/(xB-xA) = (y-yA)/(yB-yA)
(x-xA)(yB-yA) - (y-yA)(xB-xA) = 0

Polinomio che ottengo sostituendo le coordinate di C:
(xC-xA)(yB-yA) - (yC-yA)(xB-xA)

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Algoritmo 2 (con area del parallelogramma)

Considero i punti A=(xA,yA), B=(xB,yB), C=(xC,yC), D=C+B-A=(xD,yD)=(xC+xB-xA,yC+yB-yA), E=(xA,yD), F=(xD,yA).

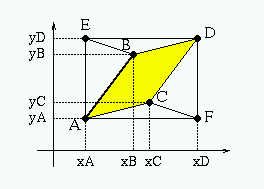
Area del parallelogramma ABDC = area del rettangolo AEDF - aree dei triangoli EAB, EBD, AFC, CFD (tutte aree con segno).

Area(AEDF) = (xD-xA)*(yD-yA) = (xC+xB-2xA)*(yC+yB-2yA).
Area(EAB) = Area(CFD) = 0.5*(xD-xC)*(yD-yA) = 0.5*(xB-xA)*(yC+yB-2yA).
Area(EBD) = Area(AFC) = 0.5*(xD-xA)*(yD-yC) = 0.5*(xC+xB-2xA)*(yB-yA).

Area(ABDC) = Area(AEDF) - 2*Area(EAB) - 2*Area(EBD) =
(xC+xB-2xA)*(yC+yB-2yA) - (xB-xA)*(yC+yB-2yA) - (xC+xB-2xA)*(yB-yA) = ...
... = (xC-xA)*(yB-yA) - (xB-xA)*(yC-yA).

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Conclusione

L'espressione di cui si valuta il segno e' il determinante
| yB-yA yC-yA |
| xB-xA xC-xA |

= (yB-yA)(xC-xA) - (yC-yA)(xB-xA)
= yA*xB - yB*xA + yC*xA - yA*xC + yB*xC - yC*xB

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Problemi numerici

Se il risultato e' molto piccolo in valore assoluto, puo' succedere che gli sia attribuito un segno errato a causa di errori di approssimazione inevitabili usando l'aritmetica floating point.

Una soluzione che di solito funziona e' quella di assumere una tolleranza epsilon>0 (molto piccola) e considerare come uguali a zero tutte le quantita' che in valore assoluto sono minori di epsilon.

In pratica si risponde che C e' allineato con A e B se la sua distanza dalla retta e' molto piccola, ovvero se l'area del parallelogramma e' molto piccola.

Complessita' temporale

Costante in quanto e' coinvolto un numero fissato di punti e di coordinate (3 e 6 rispettivamente).

Determinazione della posizione di un punto rispetto ad un triangolo

Siano A, B, C i tre vertici di un triangolo nel piano, ordinati in modo tale che la terna A,B,C svolti in senso antiorario.
Sia P un altro punto. P sta dentro, fuori, o sul contorno del triangolo ABC?

P giace dentro ABC se P sta a sinistra di tutte e tre le rette orientate definite da AB, BC, CA.
P giace fuori ABC se P sta a destra di almeno una delle tre le rette orientate sopra dette.
P giace sul contorno di ABC se P e' allineato con almeno una delle tre rette sopra dette, e giace a sinistra delle rimanenti. In particolare:
- se P e' allineato con una e a sinistra delle altre due allora P giace all'interno di un lato
- se P e' allineato con due e a sinistra della terza allora P coincide con un vertice

Complessita' temporale

Costante in quanto si riduce ad al piu' tre chiamate alla primitiva che controlla l'orientamento di una terna di punti, ciascuna chiamata avente un costo costante.

Triangolazione di un poligono semplice

Triangolazione: insieme finito di triangoli tali che, per ogni coppia di triangoli distinti t1 e t2

o t1 e t2 sono disgiunti
o condividono esattamente un lato e i suoi due vertici estremi
o condividono esattamente un vertice

Triangolazione di un poligono semplice: triangolazione tale che

l'insieme dei vertici coincide con l'insieme dei vertici del poligono
l'unione dei triangoli coincide con la regione poligonale delimitata dal poligono

Notare la differenza con la triangolazione di un insieme di punti, dove l'unione dei triangoli copre sempre il guscio convesso:

Teorema: ogni poligono semplice ammette una triangolazione.

Dimostrazione: per induzione sul numero n di lati del poligono

Se n=3, allora la triangolazione ha un solo triangolo coincidente con il poligono stesso
Se n e' maggiore di 3, allora il poligono ammette sempre una diagonale interna. Tale diagonale divide il poligono in due parti, ciascuna delle quali ha un numero di lati strettamente minore di n e quindi (per ipotesi induttiva) ammette una triangolazione. L'unione delle due triangolazioni e' una triangolazione del poligono iniziale.

Proprieta': In particolare ogni poligono con piu' di 3 lati ammette una diagonale interna tale che uno dei due sottopoligoni in cui e' diviso da tale diagonale sia un triangolo.
Tale sottopoligono triangolare e' chiamato un orecchio.

Tale proprieta' e' la base dell'algoritmo di triangolazione.

Algoritmo

INPUT: un poligono semplice Pigreco di n vertici V0,V1,...Vn-1
OUTPUT: una triangolazione Tau di Pigreco

Idea: restringo il poligono tagliando via un orecchio alla volta fino a rimanere con un solo triangolo. Ogni orecchio tagliato e il triangolo finale vanno a costituire la triangolazione.

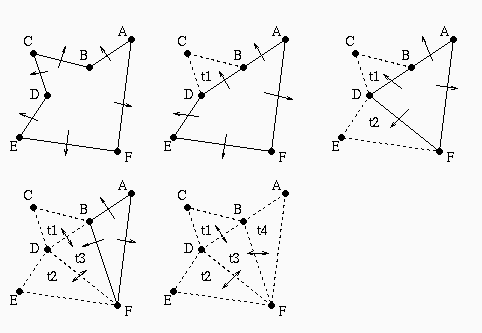
Esempio passo per passo:

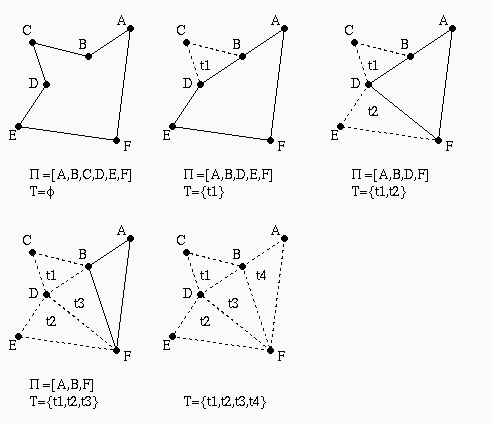
Algoritmo

Tau := empty set;
finche' numero vertici in Pigreco e' maggiore di 3
  trova un orecchio, formato da tre vertici 
        consecutivi v1,v2,v3 di Pigreco;
  aggiungi il triangolo v1,v2,v3 in Tau;
  aggiorna Pigreco rimuovendo v2;
aggiungi Pigreco (che e' un triangolo) in Tau;

Ricerca dell'orecchio

Per ogni terna di vertici consecutivi v1, v2, v3 del poligono, controllo se il segmento v1-v3 e' una diagonale interna:

In caso negativo, proseguo la ricerca spostando la terna v1, v2, v3 in avanti (ogni vi viene sostituito col suo successore).
In caso positivo, v1, v2, v3 formano un orecchio, e la ricerca termina.

Nota bene:

Dopo avere trovato un primo orecchio, e avere aggiornato triangolazione e poligono, si intraprende una seconda ricerca e cosi' via fino alla condizione di arresto.

E' importante che ogni nuova ricerca parta non dall'inizio del poligono, ma dal punto dove si era arrestata la ricerca precedente: deve partire dalla prima terna non ancora controllata. Se v1, v2, v3 e' l'orecchio appena ritagliato (v2 e' il vertice appena cancellato), allora la prima terna non controllata e' quella di vertici v0 v1 v3 dove v0 e' il predecessore di v1.

Riscriviamo l'algoritmo

Tau := empty set;
v1 := primo vertice di Pigreco;
finche' numero vertici in Pigreco e' maggiore di 3
  v2 := successore di v1 in Pigreco;
  v3 := successore di v2 in Pigreco;
  if (la terna v1,v2,v3 svolta in senso antiorario) and
     (il segmento v1-v3 e' diagonale di Pigreco)
  then 
     aggiungi il triangolo v1,v2,v3 in Tau;
     aggiorna Pigreco rimuovendo v2;
     v1 := predecessore di v1 in Pigreco;
  else v1 := successore di v1 in Pigreco;
aggiungi Pigreco (che e' un triangolo) in Tau;

Controllo se il segmento v1-v3 e' diagonale

Sappiamo gia' che v1,v2,v3 sono consecutivi sul poligono e definiscono una svolta in senso antiorario.

Quindi e' sufficiente controllare che nessun vertice di Pigreco situato fra v3 e v1 (esclusi) sia interno al triangolo v1v2v3.

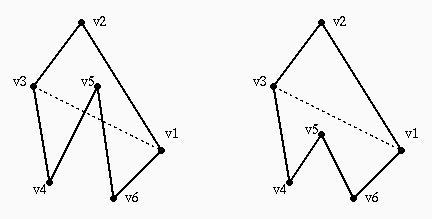
Utilizziamo a questo scopo la primitiva di test punto-in-triangolo vista precedentemente.

Struttura dati per il poligono

Struttura permanente:
Il poligono viene letto e memorizzato in un array i cui elementi sono punti (coppie di float rappresentanti le coordinate x ed y).

Struttura ausiliaria "di lavoro":
Il poligono viene copiato in una lista circolare linkata doppia. Questa lista viene aggiornata man mano che, durante l'algoritmo, si tagliano orecchie del poligono, fino ad arrivare ad una lista con soli tre elementi.
Gli elementi della lista sono numeri interi: gli indici dei corrispondenti vertici nell'array di cui sopra.

L'uso di una lista circolare linkata doppia consente di avere cancellazione in tempo costante.

Struttura dati per la triangolazione

Per ora il programma non memorizza i triangoli. Si limita stampare la lista delle diagonali da tracciare per triangolare il poligono.

Per compito:

Modificare il programma aggiungendo l'implementazione di una struttura dati per triangolazioni: la struttura triangle-based. Struttuta triangle-based

memorizza vertici e triangoli (entita' V e T)
per ogni vertice:
- le coordinate x e y
- il riferimento ad uno dei triangoli incidenti nel vertice (relazione VT* = VT parziale)
per ogni triangolo:
- i riferimenti ai tre vertici (relazione TV)
- i riferimenti ai tre triangoli adiacenti (relazione TT)
Nota: l'ordine in cui sono memorizzati i tre vertici nella TV e i tre triangoli nella TT devono essere correlati da una opportuna convenzione. Esempi: l'i-esimo triangolo della TT e' l'adiacente opposto all'iesimo vertice della TV, oppure l'i-esimo triangolo della TT e' l'adiacente lungo il lato avente come estremi l'i-esimo e l'(i+1)-esimo vertice della TV,... Scegliere una convenzione ed essere consistenti con quella.

Note:

All'inizio dell'algoritmo sappiamo gia' il numero di vertici (e' il numero di vertici del poligono), e abbiamo gia' i vertici (sono i vertici del poligono), manca solo la relazione VT*.

All'inizio dell'algoritmo sappiamo gia' anche il numero di triangoli che saranno creati (uguale al numero di vertici del poligono, meno due), mentre tutte le informazioni riguardanti i triangoli (TV e TT) andranno determinate man mano.

Il fatto che sappiamo gia' il numero di vertici e di triangoli permette di implementare la struttura dati mediante array (almeno un array per i vertici ed uno per i triangoli), senza ricorrere a strutture dinamiche come liste linkate.

Durante l'algoritmo, ad ogni "taglio di orecchio" si crea un nuovo triangolo t. E' facile determinare la relazione TV per tale triangolo.
E' anche possibile determinare la relazione TT per quanto riguarda le adiacenze del nuovo triangolo t con triangoli gia' creati.
Il triangolo t condivide due lati con il poligono corrente. t diventa adiacente ai due triangoli (se esistono) che sono gia' stati tagliati lungo tali lati.
Per recuperare i suddetti triangoli adiacenti e' sufficiente mantenere, oltre alla lista dei vertici del poligono corrente Pigreco, anche la lista dei triangoli creati esternamente adiacenti ai lati di Pigreco.

Evoluzione dei legami di adiacenza durante l'esempio visto prima (le frecce che puntano a niente sono intese come puntatori nulli):

CHE COSA VI DIAMO / CHE COSA DOVETE FARE

Che cosa vi diamo

Tutto il codice e' impacchettato nel file ese1.tgz. Scompattandolo con tar xzf ese1.tgz si crea una directory chiamata ESE1 e contenente i seguenti file:

Sorgenti C del programma "triangolazione di poligono semplice":
- list.h, list.c: implementazione della lista circolare linkata doppia di interi che implementa la copia "di lavoro" del poligono
- point.h, point.c: il tipo "punto" (coppia di coordinate float), le primitive sulle svolte (Left, LeftOn, OnLine), e la primitiva che verifica se un punto sia esterno ad un triangolo (OutTriangle)
- tripolig.c: funzioni di lettura e scrittura del poligono (ReadPoints e WritePoints), la primitiva che verifica se un segmento candidato a "tagliare un orecchio" sia una diagonale del poligono (NoCross), la funzione di triangolazione(Triangulate), e main
Sorgenti C di alcuni programmi di utilita', e file di esempio:
- vispolig.c: programma che accetta l'input o l'output di tripolig (ovvero un poligono ed eventualmente un elenco di diagonali da tracciare) e lo visualizza
- p1.pol, p2.pol, p3.pol: esempi di poligoni in input
- vistr.c: programma che accetta una triangolazione e la visualizza (ved. sezione "Che cosa bisogna fare" sotto)
- t1.tr, t2,tr, t3.tr: esempi di triangolazioni (corrispondenti ai poligoni p1.pol, p2.pol, p3.pol) scritte nel formato accettato da vistr.c.
makefile

Nota: nello stato attuale la funzione Triangulate stampa semplicemente le diagonali da tracciare, senza costruire effettivamente la triangolazione.

Che cosa bisogna fare

Implementare la struttura triangle-based e modificare Triangulate in modo tale da memorizzare la triangolazione del poligono in tale struttura.
Fornire sulla struttura le seguenti primitive per ottenere:
- il punto (informazione geometrica) corrispondente a un vertice
- il triangolo associato a un vertice mediante la VT*
- i tre vertici associati a un triangolo dalla TV
- i tre triangoli associati a un triangolo dalla TT
Queste primitive saranno utili negli esercizi successivi.
Fare stampare dall'algoritmo la lista delle entita' V e T con le loro relazioni secondo la seguente sintassi:
- numero vertici
- lista coppie x y per ogni vertice
- numero triangoli
- lista terne di vertici in relazione TV per ogni triangolo
- lista triangoli in relazione VT* per ogni vertice
- lista terne di triangoli in relazione TT per ogni triangolo
Verificare che la struttura triangle-based sia costruita correttamente operando come segue:
- usare il programma vistr.c (ved. sopra), che consente di controllare la geometria ma non le relazioni TT e VT*
- verificare manualmente che tutte le relazioni siano state memorizzate correttamente
Fornire una valutazione della complessita' spaziale e temporale dell'algoritmo di triangolazione in funzione del parametro n = numero di vertici del poligono Pigreco in input.
- valutazione dell'occupazione spaziale delle strutture permanenti (poligono, triangolazione) e di quelle ausiliarie (lista circolare, eventuali altre)
- valutazione del costo temporale delle funzioni ausiliarie (NoCross, ed eventuali altre per la costruzione della struttura triangle-based) e del costo di Triangulate
Nota bene: non dettagliare cose banali, ma spiegare i punti chiave

Che cosa bisogna consegnare

Entro il 10 maggio 1999 occorre consegnare:

I sorgenti del programma modificato, il makefile, e (facoltativamente) l'eseguibile. Si prega di scrivere codice ANSI-C (o, volendo, C++).
Una breve documentazione contenente la descrizione dell'implementazione realizzata e le valutazioni di complessita' richieste.