NOTE AL SECONDO ESERCIZIO DI LABORATORIO
Problema affrontato
Localizzazione di un punto in una triangolazione piana:
Data una triangolazione Tau (fissata) e un punto P (che cambia
di volta in volta), determinare il triangolo di Tau (se esiste)
in cui cade P.
Modalita' di soluzione
Preprocessiamo Tau costruendovi sopra un tipo particolare
di quadtree che facilita la ricerca del triangolo contenente P.
Ingredienti
- 1. Algoritmo che costruisce una triangolazione
- 2. Struttura dati triangle-based per triangolazione
- 3. Algoritmo che costruisce il quadtree per una
triangolazione
- 4. Algoritmo che cerca un punto in una triangolazione
avvelendosi del quadtree ad essa sovrapposto
Avete gia' codice per 1 e 2 (realizzati come primo
esercizio di laboratorio).
Vi diamo scheletro codice per 3, da completare usando le primitive
relative alla vostra implementazione della struttura
triangle-based.
Dovrete scrivere il codice per 4.
Maggiori dettagli su che cosa dovete fare in fondo.
Queste note spiegano
- quadtree per supporto a point location
in triangolazione
- costruzione di un quadtree
- point location in triangolazione usando quadtree
Quadtree per supporto a point location in triangolazione
Quadtree
Albero quaternario in cui sciascun nodo corriponde ad
un'area rettangolare nel piano
- la radice corrisponde ad un rettangolo arbitrario
- un nodo non foglia ha esattamente 4 figli,
il suo rettangolo e' ripartito fra i figli secondo i
4 quadranti nord-est, nord-ovest, sud-est, sud-ovest
Quadtree per triangolazioni
Quadtree costruito a partire da una triangolazione Tau
nel modo seguente:
-
Si parte da un quadtree fatto dal solo nodo radice,
il cui rettangolo e' abbastanza grande da contenere tutta
la triangolazione Tau
-
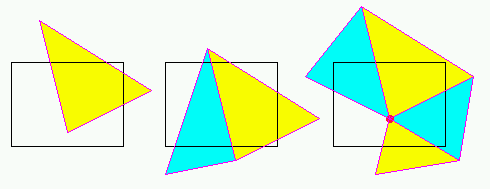
Si continua a suddividere ciascun nodo in 4 figli, fino ad
arrivare ad una delle seguenti condizioni di arresto:
- a. il rettangolo del nodo corrente e' intersecato da un solo
triangolo di Tau
- b. il rettangolo del nodo corrente e' intersecato da
due soli triangoli di Tau
- c. il rettangolo del nodo corrente contiene un unico vertice
di Tau, ed e' intersecato da k > 2 triangoli tutti incidenti
in tale vertice
- d. il rettangolo del nodo corrente non contiene alcun triangolo
Classifichiamo le foglie in base alla condizione di arresto che
le ha generate:
- condizione a ---> foglia di tipo UN_TRIANGOLO
- condizione b ---> foglia di tipo DUE_TRIANGOLI
- condizione c ---> foglia di tipo VERTICE
- condizione d ---> foglia di tipo VUOTO
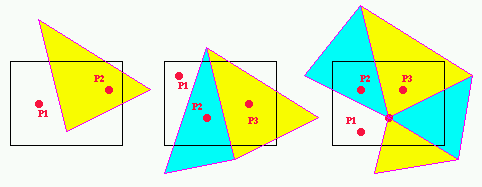
Supponendo di sapere che un punto P (il punto da localizzare)
si trova in una data foglia del quadtree, allora possiamo
calcolare facilmente in quale triangolo di Tau cade.
A seconda del tipo di foglia:
- a. UN_TRIANGOLO: P si trova o nel triangolo, oppure fuori
dal dominio della triangolazione
(un test punto-in-triangolo)
- b. DUE_TRIANGOLI: P si trova o in uno dei due triangoli,
oppure fuori dal dominio
(al piu' due test punto-in-triangolo)
- c. VERTICE: P si trova o in uno dei k triangoli
che condividono il vertice, oppure fuori dal dominio
(al piu' k test punto-in-triangolo)
- d. VUOTO: P e' fuori dal dominio della triangolazione
Implementazione del quadtree
Implementazione standard per alberi quaternari, piu' collegamenti
alla triangolazione Tau memorizzati nelle foglie.
Ogni foglia memorizza il suo tipo e, a seconda del tipo:
- a. una foglia UN_TRIANGOLO ha un puntatore al triangolo relativo
- b. una foglia DUE_TRIANGOLI ha un puntatore ai due
triangoli relativi
- c. una foglia VERTICE ha un puntatore al vertice relativo
- d. una foglia VUOTA non ha puntatori aggiuntivi

Costruzione del quadtree per triangolazioni
INPUT: una triangolazione tau
OUTPUT: un quadtree T
Idea
Si segue lo schema top-down riportato sopra.
Si parte con un albero "tentativo" fatto dalla sola radice e
si suddivide ricorsivamente fino al raggiungimento delle
condizioni di arresto.
Ad ogni passo abbiamo un nodo corrente (che dobbiamo determinare se sara'
una foglia oppure sara' suddiviso), e
un insieme di vertici e triangoli "da collocare" nel nodo corrente
(se sara' foglia) o nel sotto-albero che lo espandera' (se sara' suddiviso).
Passo generico
INPUT:
- il nodo corrente N
- un insieme V di vertici da collocare
- un insieme T di triangoli da collocare
OUTPUT:
- il sotto-quadtree finale con radice N (che potra'
eventualmente essere fatto da un solo nodo)
Algoritmo
-
se sia V che T sono vuoti ---> N diventa foglia VUOTA
-
se T ha un solo elemento ---> N diventa foglia UN_TRIANGOLO
con associato l'unico triangolo presente in T
-
se T ha due soli triangoli
---> N diventa foglia DUE_TRIANGOLI con associati
quei due triangoli
-
se V ha un solo vertice, e tutti i triangoli in T sono incidenti in
quel vertice
---> N diventa foglia VERTICE con associato l'unico vertice di V
-
altrimenti, si creano i 4 figli N1, N2, N3, N4 di N.
Per ogni figlio Ni:
- si calcola il sottoinsieme Vi di V formato dai vertici
che cadono nel rettangolo corrispondente ad Ni
- si calcola il sottoinsieme Ti di T formato dai triangoli
che intersecano il rettangolo corrispondente ad Ni
- si richiama l'algoritmo ricorsivamente su Ni, Vi e Ti
Nota: gli insiemi Vi e Ti di figli diversi possono non
essere disgiunti.
Chiamata iniziale
Inizialmente, l'algoritmo viene chiamato con N = la radice
del quadtree da creare e V, T = l'insieme di tutti i vertici,
tutti i triangoli di Tau.
Primitive geometriche
Per distribuire gli elementi di V e T tra i figli del
nodo corrente, servono
primitive per classificare un vertice, un lato e un triangolo
rispetto al rettangolo di un nodo.
Nota: il confronto lato-con-rettangolo non compare nell'algoritmo
descritto sopra, ma serve come sottocomponente del
confronto triangolo-con-rettangolo.
Sia R il nostro rettangolo e siano (Xmin,Ymin), (Xmax,Ymax) le
sue coordinate estreme.
Contenimento vertice-in-rettangolo
Un punto P=(x,y) cade nel rettangolo R sse
Xmin < x < Xmax e Ymin < y < Ymax.
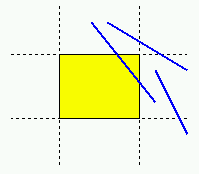
Intersezione lato-con-rettangolo
Siano p1 e p2 gli estremi del lato.
- se p1, p2 hanno entrambi ascissa < Xmin
---> il lato non puo' intersecare R
- se p1, p2 hanno entrambi ascissa > Xmax
---> il lato non puo' intersecare R
- se p1, p2 hanno entrambi ordinata < Ymin
---> il lato non puo' intersecare R
- se p1, p2 hanno entrambi ordinata > Ymax
---> il lato non puo' intersecare R
- altrimenti, il lato interseca R sse fra i vertici di R ve ne
sono due tali che uno sta a
destra e l'altro a sinistra rispetto al lato
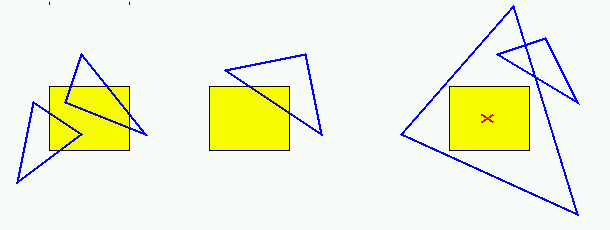
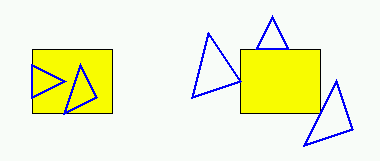
Intersezione triangolo-con-rettangolo
Sia t un triangolo di vertici p1,p2,p3.
- se almeno uno fra p1, p2, p3 cade nel rettangolo R
---> t interseca R
- altrimenti,
se almeno uno dei lati di t interseca il rettangolo R
---> t interseca R
- altrimenti, t puo' essere completamente disgiunto
da R, oppure contenere completamente R.
t contiene R e' sse un punto di R (per esempio il
baricentro) e' interno a t
Casi particolari
Nei problemi geometrici tipicamente i casi particolari sono vari e
laboriosi da trattare.
- vertice che giace sul contorno del rettangolo R
(eventualmente coincidente con uno dei quattro angoli di R)
- triangolo tangente internamente ad R
- triangolo tangente esternamente ad R
Eliminiamo molti problemi con la seguente assunzione
(fatta solo a scopo didattico, non realistica, non ammissibile
in un programma per applicazioni "vere"):
Tutte le coordinate dei vertici della triangolazione data
o sono intere, o hanno una sola cifra decimale significativa,
uguale a 5.
Le ascisse ed ordinate dei rettangoli del quadtree hanno tutte
parti decimali uguali a .3+W dove W e' una potenza di 2
(... 4, 2, 1, 0.5, 0.25 ...).
In questo modo, un vertice non cadra' mai sul contorno di un
rettangolo, un triangolo non potra' mai essere tangente
internamente ad un rettangolo.
Un triangolo puo' essere tangente esternamente ad un rettangolo
ma solo nella configurazione "angolo del rettangolo giacente
all'interno di un lato del triangolo".
In questa configurazione il triangolo viene riconosciuto
correttamente esterno al rettangolo purche' il confronto
lato-con-rettangolo sia eseguito in modo stretto (ritornando
"intersezione" solo in caso di intersezione propria).
Limite alla profondita' dell'albero
Nel caso di triangoli molto sottili e allungati, puo' essere
necessario dividere moltissimo prima di giungere ad una delle
configurazioni di arresto, e in tutte le configurazioni che
si attraversano prima di arrivarvi magari ci sono solo pochi
triangoli.
Suddividere troppo a fondo aumenta la profondita' dell'albero e
quindi la complessita' della ricerca.
E' preferibile avere una foglia con 3 o 4 triangoli piuttosto che
avere una foglia con uno o due triangoli preceduta da un cammino
di parecchi nodi.
Percio' si pone una profondita' massima al di la' della quale non si
suddivide piu': il nodo corrente diviene foglia di tipo STOP,
e tutti i triangoli che lo intersecano (= i triangoli
correntemente "da collocare") sono associati al nodo.
Qui profondita' max = 6, nodi UN_TRIANGOLO rossi, DUE_TRIANGOLI magenta,
VERTICE blu, VUOTI neri, STOP verdi:

Point location su triangolazione usando quadtree
Due fasi:
-
ricerca nel quadtree della foglia contenente il punto P
-
ricerca del triangolo contenente P (se esiste) fra quelli
"suggeriti" dalla foglia.
Ricerca della foglia
Si parte dalla radice.
Se il nodo corrente N e' una foglia, fine.
Altrimenti si determina quale dei figli di N
contiene P, e si prosegue su tale figlio.
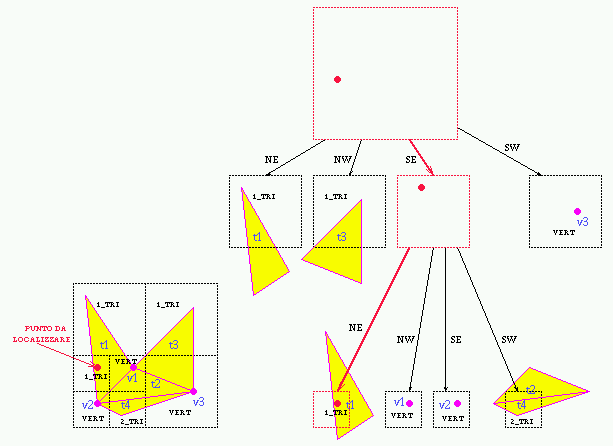
Ricerca del triangolo nella foglia
A seconda del tipo di foglia:
- foglia VUOTA: un triangolo contenente P non esiste,
P e' esterno al dominio della triangolazione
- foglia TRIANGOLO:
si controlla se P e' contenuto nel triangolo t associato;
in caso positivo, si ritorna t;
altrimenti, un triangolo contenente P non esiste
- foglia LATO:
si controlla se P e' contenuto in uno dei due triangoli
t1 e t2 associati;
in caso positivo, si ritorna ti;
altrimenti, un triangolo contenente P non esiste
- foglia VERTICE:
si controlla se P e' contenuto in uno dei triangoli ti
incidenti nel vertice;
in caso positivo, si ritorna ti;
altrimenti, un triangolo contenente P non esiste
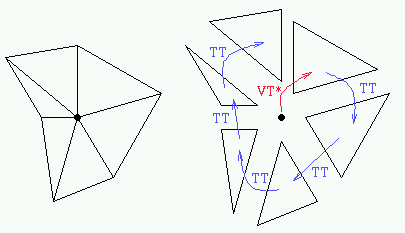
Per trattare il caso di foglia VERTICE, e' necessario
usare le relazioni memorizzate nella struttura triangle-based
per trovare i triangoli incidenti in un vertice v.
La relazione VT parziale fornisce il primo triangolo.
Ogni triangolo si trova dal precedente selezionando dalla relazione
TT l'adiacente che condivide v avendo cura di muoversi sempre
nello stesso senso (orario o antiorario) attorno a v.
Casi particolari
- il punto da localizzare coincide con un vertice o giace su
un lato della triangolazione --> il triangolo
che lo contiene non e' univocamente definito
- il punto da localizzare giace sul contorno di un rettangolo
di un nodo --> c'e' ambiguita' riguardo a quale figlio
scendere per proseguire la visita dell'albero
Ancora a scopo semplificativo e didattico, assumiano che
il punto dato non dia luogo a casi particolari.
CHE COSA VI DIAMO / CHE COSA DOVETE FARE
Che cosa vi diamo
Tutto il codice e' impacchettato nel file
ese2.tgz.
Scompattandolo con tar xzf ese2.tgz si crea una
directory chiamata ESE2 e contenente i seguenti file:
-
Sorgenti C del programma "costruzione di quadtree per triangolazione":
- stack.h, stack.c:
implementazione a stack dell'insieme di vertici e dell'insieme
di triangoli "da collocare" nel nodo corrente durante la
costruzione
- tree.h, tree.c: il tipo "quadtree", albero quaternario
ai cui nodi possono essere associati vertici e triangoli
- une nuova versione dei files point.h e point.c: rispetto
al primo esercizio, e' stata aggiunta la funzione InTriangle
(che controlla se un punto e' strettamente contenuto in
un triangolo) ed e' stato corretto un baco (la funzione abs()
e' stata sostituita con fabs() nella macro per Equal).
- build.c:
- funzioni di lettura della triangolazione e di scrittura del
quadtree
(ReadTriangulation e PrintQuadtree)
- primitive geometriche per classificare un vertice, lato,
triangolo rispetto ad un rettangolo
(pointInBox, edgeInBox, triangleInBox)
- funzione che estrae i vertici/triangoli dell'insieme
corrente che sono contenuti/intersecano un nodo
(clipElements)
- funzione ricorsiva di costruzione (Build) e
funzione di costruzione a livello esterno che la
richiama (BuildQuadtree)
- main
-
Sorgenti C dei programmi di utilita':
- visqtree.c:
accetta una triangolazione ed un quadtree
(output del primo esercizio e output di build, rispettivamente)
e li visualizza
- visptloc.c:
accetta una triangolazione, un punto e un triangolo, e
visualizza il punto, la triangolazione con evidenziato
il triangolo dato
- makefile
NOTA:
Nello stato attuale le varie funzioni definite in "build.c"
hanno delle parti "in sospeso" che
vanno completate con le primitive relative alla vostra
implementazione della struttura dati triangle-based.
Che cosa bisogna fare
- Completare il programma di costruzione inserendo le
primitive relative alla propria implementazione della struttura
dati triangle-based.
Le parti da completare sono segnate con commenti preceduti
dalla parola "COMPLETARE".
- Implementare l'algoritmo di point location.
- Far stampare al programma che implementa l'algoritmo
di point location un file contenente la triangolazione,
il punto, e il triangolo determinato come risposta
secondo la seguente sintassi:
- per la triangolazione, come la volta scorsa
- per il punto: INPUT_POINT x y
dove x e y sono due float
- per il triangolo: OUTPUT_TRIANGLE i
dove i e' l'indice intero del triangolo
nella triangolazione
- Verificare che gli algoritmi di costruzione e di point location
funzionino, aiutandosi anche con i programmi di visualizzazione
forniti (ved. dopo).
- Fornire una valutazione della complessita' spaziale
del quadtree.
- Fornire una valutazione della complessita' temporale
dell'algoritmo di point location.
Nota sulle complessita':
Per semplicita' assumere che non vi siano nodi STOP.
Parametri utili sono h = profondita' massima stabilita per il quadtree,
n = numero di triangoli in Tau, k = numero massimo di triangoli
incidenti in un vertice.
Nota bene: non dettagliare cose banali, ma spiegare i punti chiave.
Che cosa bisogna consegnare
Entro il 2 giugno 1999 (per coloro che intendono dare l'esame
a giugno) o il 7 giugno 1999 (per gli altri) occorre consegnare:
- I sorgenti del programma, il makefile, e
(facoltativamente) l'eseguibile.
Si prega di scrivere codice ANSI-C (o, volendo, C++).
- Una breve documentazione contenente la descrizione
dell'implementazione realizzata e le valutazioni di complessita'
richieste.









