Boundary representations (B-Reps)

Descrivono un oggetto solido mediante il suo contorno.
Il contorno di un solido e' un 2-manifold senza boundary.
Il contorno viene rappresentato con un complesso cellulare 2-dimensionale.
Il contorno puo' essere fatto da piu' componenti connesse (es: solido con una cavita' interna che non comunica con l'esterno). Ciascuna componente connessa e' chiamata un guscio (shell). Ci sono una shell esterna e zero o piu' shell interne.
Rappresentiamo ciascuna shell separatamente (un complesso cellulare per ogni shell).
Il contorno di un oggetto e' orientabile (ha un interno e un esterno ben definiti). Nel complesso cellulare che lo descrive si orientano le facce, di solito in modo tale che la normale alla faccia punti verso l'esterno.
Questo significa che il ciclo di spigoli che contorna la faccia e' orientato in modo tale da essere visto in senso antiorario da un osservatore che guarda l'oggetto da fuori.
L'orientamento della shell esterna e quello delle shell interne sono opposti.

Descrizione della geometria

In una suddivisione piana, assumendo lati rettilinei, le sole entita' che necessitano una descrizione geometrica sono i vertici. Per ogni vertice servono 2 coordinate.

In un complesso cellulare immerso nello spazio, ciascun vertice ha 3 coordinate. Inoltre si pone il problema di descrivere la geometria delle facce.

Anche se assumiamo spigoli rettilinei, non e' detto che gli spigoli di contorno di una faccia descrivano la faccia come un poligono piano. Questo e' garantito solo se la faccia ha tre spigoli (triangolo).
Se ammettiamo facce non piane, queste necessitano di una descrizione della loro geometria. Inoltre in questo caso e' sensato ammettere anche spigoli non rettilinei.

Primo modo: solo facce piane

Si ammettono solo spigoli rettilinei e facce piane. Allora la geometria del complesso cellulare e' univocamente determinata dalle posizioni dei vertici. Come nel caso piano, non e' necessario associare informazioni geometriche a spigoli e facce.

Le facce devono essere triangoli. Il complesso e' un complesso simpliciale.

Rappresentazioni di questo tipo si usano per visualizzazione grafica (il triangolo e' la primitiva base per i dispositivi di rendering), e per altre applicazioni che necessitano di lavorare su facce con geometria semplice (es: analisi agli elementi finiti).

Pro: struttura dati semplice, elaborazioni sulla singola faccia si effettuano in tempo costante.
E' il formato usato da strumenti di acquisizione (scanner 3D) e di visualizzazione (schede grafiche).
Contro: servono moltissime facce per descrivere accuratamente la forma di un oggetto, cio' incide su spazio di memorizzazione e tempo di elaborazione totale.

Secondo modo: facce e spigoli arbitrari

Si ammettono spigoli non rettilinei e facce non piane. Ogni spigolo e ogni faccia necessita di una descrizione della sua geometria = equazione della curva o della superficie a cui appartiene.

Spesso si tengono descrizioni per le facce, e la geometria degli spigoli e' indotta da quella delle facce (spigolo = intersezione di due facce).

Rappresentazioni implicite: una equazione della forma f(x,y,z)=0.
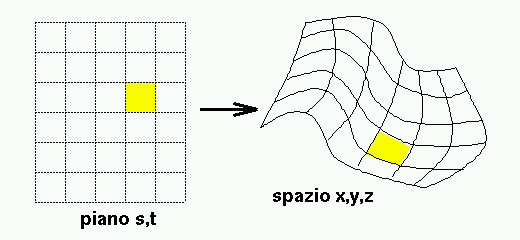
Rappresentazioni parametriche: tre equazioni della forma x=f1(s,t), y=f2(s,t), z=f3(s,t) dove s,t sono i due parametri. E' una funzione che mappa un dominio del piano (s,t) nello spazio 3D.

Le rappresentazioni parametriche sono le piu' usate. Di solito f1, f2, f3 sono funzioni razionali (rapporti fra polinomi), e sono definite come combinazione di certe funzioni base.

Classi di funzioni usate: Curve e superfici di Bezier, B-Splines, NURBS (Non-Uniform Rational B-Splines).

In (s,t) il dominio e' un rettangolo.
Tale rettangolo e' diviso in maglie da una griglia.
La funzione fi e' definita a pezzi in ciascuna maglia della griglia.
L'espressione di fi in una maglia della griglia dipende da pochi parametri comuni solo a quella maglia e alle maglie sue vicine (definizione locale).

La forma della superficie si puo' controllare agendo su punti di controllo: punti che sono in corrispondenza con gli incroci della griglia, non sono necessariamente interpolati dalla superficie, ma determinano i parametri in base ai quali la superficie viene calcolata.
Spostando un punto di controllo la forma della superficie cambia localmente alle maglie interessate.

Le funzioni fi non sono necessariamente univoche. Piu' punti (s,t) possono avere stessa immagine nello spazio, definendo cosi' superfici che si ripiegano su se stesse (cilindro, cono, toro...).

In casi piu' generali il dominio in (s,t) e' ottenuto ritagliando il rettangolo con lati rettilinei o curvi (trimmed NURBS). Nel caso di lati curvi, ciascun lato e' definito a sua volta in forma parametrica.

Pro: servono poche facce per descrivere accuratamente la forma di un oggetto, la rappresentazione e' concisa.
E' facile costruire modelli interattivamente con un sistema CAD (si colloca la griglia, si spostano i punti di controllo finche' la superficie assume la forma desiderata).
Contro: elaborazioni su una faccia sono difficili, spesso bisogna discretizzare le facce in triangoli per poterle trattare (es: visualizzazione grafica), problemi di inconsistenza geometrica tra facce adiacenti (ved. sotto).

Inconsistenza geometrica

La geometria di un lato e' definita implicitamente da quella delle facce a cui appartiene, ed e' definita in ciascuna delle due facce in modo indipendente. Non sempre la geometria del lato coincide esattamente nelle due facce, per cui le due facce possono non combaciare.
Nei modellatori esistenti sono comuni effetti come spaccature o sovrapposizioni parziali o intersezioni tra facce che dovrebbero essere adiacenti.

Facce con buchi

Un oggetto solido puo' avere fori passanti che lo attraversano, e/o fori che definiscono cavita'.

Tipicamente, l'imbocco di un foro segna un buco su una faccia. Tale faccia non e' piu' omemomnorfa a un disco, ma e' una regione piana con buchi. Dunque il contorno del solido non e' piu' descrivibile come un complesso cellulare (le facce non sono celle).

Due alternative:

Dividiamo le facce con buchi in parti che siano celle (omeomorfe a dischi), che diventano le facce della nostra rappresentazione.
Generalizziamo la definizione di complesso cellulare ammettendo facce con buchi (cella generalizzata = 2-manifold connesso con contorno).

Nel primo caso la suddivisione delle facce e' arbitraria e puo' sembrare una forzatura. Ci consente di lavorare con complessi cellulari e di usare le relative strutture dati.

Nel secondo caso occorre estendere le strutture dati viste per complessi cellulari in modo da poter rappresentare complessi dove le facce contengono buchi.

In una faccia con buchi, il contorno ha piu' componenti connesse. Ciascuna componente e' chiamata un ciclo (loop). Una faccia ha un loop esterno e zero o piu' loop interni.

Estensione delle strutture dati per trattare facce con buchi

estensione della struttura dati simmetrica
estensione della struttura dati winged-edge

Introduciamo una nuova entita' (entita' derivata): il loop. Simbolo: L.

Ciascuna faccia ha uno o piu' loop, ciascun loop e' composto da una sequenza circolare di spigoli.

Ciascuno spigolo appartiene a un loop di una faccia e a un loop di un'altra faccia.

Nota: un loop puo' essere comune a due facce, anche se raramente.

Interponiamo il loop come entita' di collegamento fra spigolo e faccia.

La relazione FE e' sostituita dalle relazioni FL e LE.
La relazione EF e' sostituita dalle relazioni EL e LF.

FL associa a una faccia tutti i loop che la contornano, per primo quello esterno.

LE associa a un loop la lista ordinata dei suoi spigoli.

EL associa ad uno spigolo i due loop che lo contengono.

LF associa a un loop le facce (di solito una, raramente due) che lo contengono.

Struttura simmetrica estesa

Le relazioni FE e EF sono sostituite da FL, LE, EL, LF.

Come ricaviamo le relazioni FE e EF?

Struttura winged-edge estesa

La relazione EF e' sostituita da EL e LF. La relazione FE* e' sostituita da FL e LE*.

Come ricaviamo la relazione FE*?