Triangolazione di un poligono semplice

Triangolazione: insieme finito di triangoli tali che, per ogni coppia di triangoli distinti t1 e t2

o t1 e t2 sono disgiunti
o condividono esattamente un lato e i suoi due vertici estremi
o condividono esattamente un vertice

Triangolazione di un poligono semplice: triangolazione tale che

l'insieme dei vertici coincide con l'insieme dei vertici del poligono
l'unione dei triangoli coincide con la regione poligonale delimitata dal poligono

Notare la differenza con la triangolazione di un insieme di punti, dove l'unione dei triangoli copre sempre il guscio convesso:

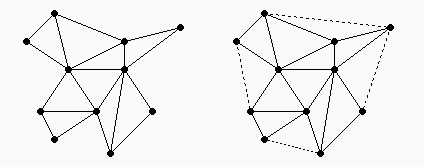
Teorema: ogni poligono semplice ammette una triangolazione.

Dimostrazione: per induzione sul numero n di lati del poligono

Se n=3, allora la triangolazione ha un solo triangolo coincidente con il poligono stesso
Se n e' maggiore di 3, allora il poligono ammette sempre una diagonale interna. Tale diagonale divide il poligono in due parti, ciascuna delle quali ha un numero di lati strettamente minore di n e quindi (per ipotesi induttiva) ammette una triangolazione. L'unione delle due triangolazioni e' una triangolazione del poligono iniziale.

Proprieta': In particolare ogni poligono con piu' di 3 lati ammette una diagonale interna tale che uno dei due sottopoligoni in cui e' diviso da tale diagonale sia un triangolo.
Tale sottopoligono triangolare e' chiamato un orecchio.

Tale proprieta' e' la base dell'algoritmo di triangolazione che vedremo.

Algoritmo

INPUT: un poligono semplice Pigreco di n vertici V0,V1,...Vn-1
OUTPUT: una triangolazione Tau di Pigreco

Idea: restringo il poligono tagliando via un orecchio alla volta fino a rimanere con un solo triangolo. Ogni orecchio tagliato e il triangolo finale vanno a costituire la triangolazione.

Esempio passo per passo:

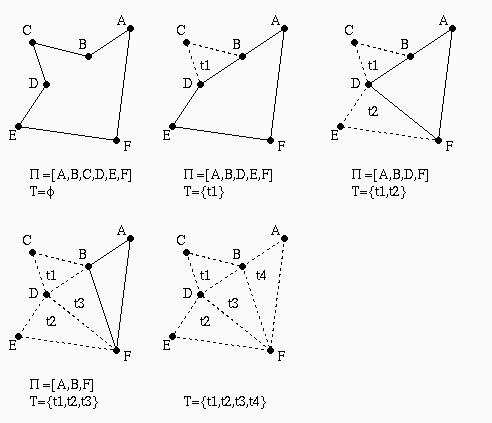
Schema generale

Tau := empty set;
finche' numero vertici in Pigreco e' maggiore di 3
  trova un orecchio, formato da tre vertici 
        consecutivi v1,v2,v3 di Pigreco;
  aggiungi il triangolo v1,v2,v3 in Tau;
  aggiorna Pigreco rimuovendo v2;
aggiungi Pigreco (che e' un triangolo) in Tau;

Ricerca dell'orecchio

Esploro il contorno del poligono per esempio in senso antiorario.

Per ogni terna di vertici consecutivi v1, v2, v3 del poligono, controllo se il segmento v1-v3 e' una diagonale interna:

In caso negativo, proseguo la ricerca spostando la terna v1, v2, v3 in avanti (ogni vi viene sostituito col suo successore).
In caso positivo, v1, v2, v3 formano un orecchio, e la ricerca termina.

Nota bene:

Dopo avere trovato un primo orecchio, e avere aggiornato triangolazione e poligono, si intraprende una seconda ricerca e cosi' via fino alla condizione di arresto.
E' importante che ogni nuova ricerca parta non dall'inizio del poligono, ma dal punto dove si era arrestata la ricerca precedente: deve partire dalla prima terna non ancora controllata. Se v1, v2, v3 e' l'orecchio appena ritagliato (v2 e' il vertice appena cancellato), allora la prima terna non controllata e' quella di vertici v0 v1 v3 dove v0 e' il predecessore di v1.

Riscriviamo l'algoritmo

Tau := empty set;
v1 := primo vertice di Pigreco;
finche' numero vertici in Pigreco e' maggiore di 3
  v2 := successore di v1 in Pigreco;
  v3 := successore di v2 in Pigreco;
  if (la terna v1,v2,v3 svolta in senso antiorario) and
     (il segmento v1-v3 e' diagonale di Pigreco)
  then 
     aggiungi il triangolo v1,v2,v3 in Tau;
     aggiorna Pigreco rimuovendo v2;
     v1 := predecessore di v1 in Pigreco;
  else v1 := successore di v1 in Pigreco;
aggiungi Pigreco (che e' un triangolo) in Tau;

Sottocomponenti dell'algoritmo

Controllo se il segmento v1-v3 e' diagonale

Sappiamo gia' che v1,v2,v3 sono consecutivi sul poligono e definiscono una svolta in senso antiorario.

Quindi e' sufficiente controllare che nessun vertice di Pigreco situato fra v3 e v1 (esclusi) sia interno al triangolo v1v2v3.

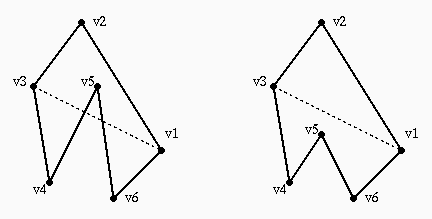
Controllo della posizione di un punto rispetto ad un triangolo

Siano A, B, C i tre vertici di un triangolo nel piano, ordinati in modo tale che la terna A,B,C svolti in senso antiorario. Sia P un altro punto.

P giace dentro ABC se P sta a sinistra di tutte e tre le rette orientate definite da AB, BC, CA.
P giace fuori ABC se P sta a destra di almeno una delle tre le rette orientate sopra dette.
P giace sul contorno di ABC se P e' allineato con almeno una delle tre rette sopra dette, e giace a sinistra delle rimanenti. In particolare:
- se P e' allineato con una e a sinistra delle altre due allora P giace all'interno di un lato
- se P e' allineato con due e a sinistra della terza allora P coincide con un vertice

Strutture dati

Struttura dati per il poligono

I vertici del poligono sono inizialmente caricati in una lista circolare linkata doppia. Questa lista viene aggiornata man mano che, durante l'algoritmo, si tagliano orecchie del poligono, fino ad arrivare ad una lista con soli tre elementi. L'uso di una lista circolare linkata doppia consente di avere cancellazione in tempo costante.

Struttura dati per la triangolazione

Utilizziamo una struttura dati per triangolazioni: la struttura triangle-based.

memorizza vertici e triangoli (entita' V e T)
per ogni vertice:
- le coordinate x e y
- il riferimento ad uno dei triangoli incidenti nel vertice (relazione VT* = VT parziale)
per ogni triangolo:
- i riferimenti ai tre vertici (relazione TV)
- i riferimenti ai tre triangoli adiacenti (relazione TT)

Nota: l'ordine in cui sono memorizzati i tre vertici nella TV e i tre triangoli nella TT devono essere correlati da una opportuna convenzione. Esempi di convenzioni:

l'i-esimo triangolo della TT e' l'adiacente opposto all'iesimo vertice della TV
l'i-esimo triangolo della TT e' l'adiacente lungo il lato avente come estremi l'i-esimo e l'(i+1)-esimo vertice della TV

Durante l'algoritmo, ad ogni "taglio di orecchio" si crea un nuovo triangolo t:

E' facile determinare la relazione TV per tale triangolo, in quanto sappiamo i tre vertici.
E' anche possibile determinare la relazione TT per quanto riguarda le adiacenze del nuovo triangolo t con triangoli gia' creati.
Il triangolo t condivide due lati con il poligono corrente. t diventa adiacente ai due triangoli (se esistono) che sono gia' stati tagliati lungo tali lati.
Per recuperare i suddetti triangoli adiacenti e' sufficiente mantenere, collegati ai lati del poligono corrente Pigreco, i triangoli creati esternamente adiacenti a tali lati.

Evoluzione dei legami di adiacenza durante l'esempio visto prima (le frecce che puntano a niente sono intese come puntatori nulli):

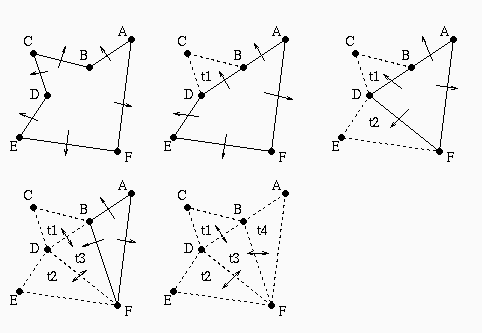
Complessita' temporale

Costo della primitiva punto-in-poligono

Costante in quanto si riduce ad al piu' tre chiamate alla primitiva che controlla l'orientamento di una terna di punti, ciascuna chiamata avente un costo costante.

Costo del controllo e'-diagonale-interna

Tante chiamate alla punto-in-poligono quanti i vertici giacenti fra v3 e v1. Tali vertici sono k-3 se il poligono correntemente ha k lati. Quindi il costo e' lineare in k.

Costo per creare un triangolo

Costante. Consiste nell'inizializzare 6 campi per TV e TT. I lavori con cui inizializzali si determinano in tempo costante.

Costo di un passo del ciclo

Dominato dal costo del controllo diagonale. Ai fini della valutazione posso maggiorarlo con O(n).

Quante volte viene eseguito il ciclo

Per triangolare un poligono di n lati e' necessario tagliare n-3 orecchie.

Nel caso migliore (poligono convesso) ad ogni passo del ciclo taglio un orecchio, il ciclo termina in n-3 passi.

Nel caso generale posso notare che:

sono eseguiti esattamente n-3 passi con taglio di un orecchio
non posso avanzare a vuoto piu' di n volte altrimenti significherebbe che non esistono orecchie da tagliare, e questo viola il teorema
siccome ad ogni taglio di orecchio torno indietro di una terna, devo riavanzare, ma questo non puo' succedere piu' di n-3 volte

In conclusione il ciclo viene eseguito un numero di volte maggiorabile con 3n = O(n).

Complessita' totale

O(n) passi del ciclo, ciascuno con un costo in O(n). Pertanto la complessita' totale e' in O(n^2).

Puo' venire il dubbio che questa valutazione sia troppo pessimista perche' la maggiorazione del costo di un passo del ciclo con O(n) e' grossolana.

Facciamo i conti fini nel caso semplificato in cui il ciclo viene eseguito n-3 volte, ogni volta tagliando un orecchio (per es. questo avviene in un poligono convesso).
Il numero di vertici del poligono corrente al passo i-esimo e' n-i, e pertanto il costo del controllo diagonale e' in O(n-i).

Quindi il costo totale e' dato da: somma per i da 1 a n-3 di O(n-i), il che e' comunque in O(n^2).

Con questo abbiamo dimostrato che la maggiorazione O(n) per costo di un passo del ciclo non influenza negativamente la valutazione totale.