Corso di Interfacce Utente - A.A. 2005-2006

PROGETTO DI LABORATORIO - DOCUMENTO 2 DI 3

Vedere la pagina principale del progetto per gli altri due documenti.

Descrizione delle classi che implementano l'applicazione "Diagramma di Voronoi"

L'applicazione e' costituita dalle seguenti classi Java:

• La classe BasicFunctions contiene alcune funzioni elementari e serve da superclasse comune ad altre classi dell'applicazione.
• La classe PointXY implementa un punto nel piano.
• La classe Voronoi implementa il diagramma di Voronoi.
• La classe Clipping implementa una funzione che serve per il disegno delle regioni di Voronoi (vedere dopo).

Classe PointXY

Costruttori:

• PointXY() Crea punto posizionato nell'origine.
• PointXY(double x, double y) Crea punto posizionato in (x,y).

Metodi:

• double getX() e double getY() Ritornano le coordinate x ed y del punto.
• void setPointXY(double x, double y) Posiziona il punto in (x,y).
• void setPointXY(PointXY p) Posiziona il punto a coincidere con p.

Classe Voronoi

I siti possono essere al massimo 150 (le regioni sono tante quante i siti).
Ogni sito ha un "nome" ovvero un numero intero non negativo che lo identifica univocamente. Quando un sito viene eliminato dal diagramma, il suo "nome" non verra' assegnato a nessun altro sito che venga inserito dopo, ma per i nuovi siti saranno usati altri numeri. Quindi in generale, in un diagramma di Voronoi con K siti, i "nomi" NON sono i numeri da 0 a K-1, ma possono essere numeri sparsi anche molto piu' grandi di K.
Siccome le regioni di Voronoi ricoprono tutto il piano, alcune si esse sono infinite, cioe' hanno dei vertici all'infinito. In pratica, quando le coordinate di un vertice sarebbero all'infinito, vengono "approssimate" con numeri molto grandi in positivo o in negativo. Questo non crea problemi fino a che non andiamo a disegnare (vedere classe Clipping dopo).

Costante:

• int MAX_NUMBER
  Massimo numero di siti che il diagramma di Voronoi puo' contenere, vale 150. Se provo ad inserire il 151-esimo sito l'inserimento fallisce.

Costruttori:

• Voronoi(double x1, double y1, double x2, double y2)
  Crea il diagramma di Voronoi con i quattro siti iniziali posizionati nei quattro angoli del rettangolo di diagonale (x1,y1)-(x2,y2).
• Voronoi()
  Come sopra, ma per default il rettangolo e' quello di diagonale (-10,-10)-(10,10).

Metodi per vedere i siti e le regioni di Voronoi:

• int number()
  Ritorna il numero di siti (che e' anche il numero di regioni) presenti nel diagramma di Voronoi.
• PointXY[] getPoints()
  Ritorna un array contenente tutti i punti che sono siti del diagramma di Voronoi.
• PointXY[] getRegion(PointXY p) e PointXY[] getRegion(double x, double y)
  Se il punto p, ovvero il punto di coordinate (x,y), e' un sito, restituisce un array di punti contenente i vertici della sua regione di Voronoi, elencati in senso antiorario. Altrimenti ritorna l'oggetto nullo.
• double getMinX(), getMinY(), getMaxX(), getMaxY()
  Restituiscono le minime e massime coordinate dei siti (sono le coordinate minime e massime del rettangolo di riferimento).

Metodi relativi ai "nomi" dei siti:

• int getName(PointXY p) e int getName(double x, double y)
  Se il punto p ovvero il punto di coordinate (x,y) e' un sito, ritorna il "nome" numerico del sito nel diagramma di Voronoi. Altrimenti ritorna -1.
• PointXY getFromName(int n)
  Ritorna il sito corrispondente al "nome" dato, se esiste un sito con quel nome. Altrimenti ritorna l'oggetto nullo.

Metodi relativi alla posizione di un punto rispetto al diagramma di Voronoi:

• boolean isInDiagram(PointXY p) e boolean isInDiagram(double x, double y)
  Se il punto p, ovvero il punto di coordinate (x,y), e' un sito, restituisce true. Altrimenti restituisce false.
• boolean moveToNearest(PointXY p, double tolerance)
  Se il punto p dista da un sito meno della tolleranza, sposta il punto p a coincidere col sito e restituisce true. Altrimenti lascia p invariato e restituisce false. Nota: nel caso che piu' siti abbiano distanza da p inferiore alla tolleranza, prende il primo che trova (quindi usare tolleranze piccole!).

Metodi per aggiungere o eliminare un sito:

• boolean insert(double x, double y)
  Se possibile, inserisce il punto (x,y) come nuovo sito nel diagramma di Voronoi. E' possibile se il punto (x,y) non e' esterno al rettangolo di riferimento e non e' gia' presente un sito nella stessa posizione (e se il numero di siti non eccede MAX_NUMBER).
  Se possibile, inserisce il punto modificando il diagramma di Voronoi (al punto sara' associata una propria regione "ritagliandola" dalle regioni dei punti ad esso piu' vicini) e ritorna true. Altrimenti non fa nulla e ritorna false.
• boolean delete(double x, double y)
  Se possibile, elimina il punto (x,y) dal diagramma di Voronoi. E' possibile se il punto (x,y) e' un sito presente nel diagramma e non e' uno dei quattro angoli del rettangolo di riferimento (che sono ineliminabili).
  Se possibile, elimina il sito modificando il diagramma di Voronoi (verra' eliminata la regione corrispondente "distribuendo" fra le regioni confinanti lo spazio che occupava) e ritorna true. Altrimenti non fa nulla e ritorna false.

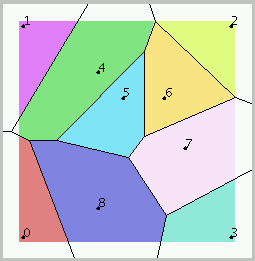
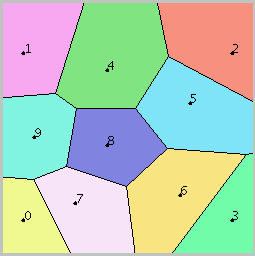
Diagramma di Voronoi prima e dopo aver inserito il punto 10 (o dopo e prima averlo cancellato):

Classe Clipping

In generale una regione di Voronoi puo' cadere in parte fuori dalla finestra grafica in cui stiamo disegnando il diagramma, avendo i suoi vertici anche coordinate molto grandi in valore assoluto (in teoria possono avere coordinate all'infinito).
Per assicurare che Java riesca a disegnare correttamente anche in questi casi, bisogna "ritagliare" le regioni: tenere di ogni regione solo la parte che sta dentro il rettangolo in cui andiamo a disegnare. Questa operazione si chiama "clipping".

La classe Clipping ha una sola funzione di classe, che serve proprio a questo:

• PointXY[] clipRegion(PointXY[] reg, double x1, double y1, double x2, double y2)
  Data la regione reg (che sara' una regione di Voronoi calcolata con getRegion della classe Voronoi), ritaglia la parte di reg che si trova dentro al rettangolo di diagonale (x1,y1)-(x2,y2) e restituisce la regione cosi' ritagliata.
  IMPORTANTE: funziona solo se rettangolo usato per ritagliare e' piu' ampio del rettangolo definito dai quattro siti d'angolo del diagramma di Voronoi.

Diagramma di Voronoi con tracciati i lati delle regioni "intere" e colorato l'interno delle regioni dopo il "clipping":