MT DELAUNAY

Terrain triangulation and construction of a Multi-Triangulation.

General Information

Program Delaunaymt allows the construction of MTs for terrains (two-dimensional scalar fields) based on a (constrained) Delaunay triangulation of the plane domain of the terrain.

Delaunaymt includes several algorithms for the construction and iterative modification of Delaunay triangulations and constrained Delaunay triangulation through vertex insertion or vertex removal. As a side effect, the program builds an MT from the sequence of local modifications performed.

The basic functionalities of the program are:

Construction of a Delaunay triangulation starting from a set of points through iterative vertex insertion, and production of an MT.
Construction of a constrained Delaunay triangulation starting from a set of points and line segments. This functionality is just meant to provide an input file for the algorithms based on vertex removal (see point 4 below), and does not produce an MT.
Decimation of a Delaunay triangulation through iterative vertex removal, and production of an MT.
Decimation of a constrained Delaunay triangulation through iterative vertex removal, and production of an MT.

Approaches 1, 3, and 4 output an MT as well as the approximation errors of its triangles. The approximation error of a triangle t is evaluated as the maximum vertical distance between a point (not vertex of the triangulation), whose vertical projection falls inside or on the boundary of t, and the plane of t.

Vertices can be inserted / removed either in a random order, or selected according to heuristic criteria which try to achieve the least approximation error for a given number of triangles in the current representation.
In the latter case, the next point to be inserted is the one that is likely to decrease the approximation error as quickly as possible, and the the next point to be removed is the one that is likely to increase the approximation error as slowly as possible.

Moreover, approaches 3 and 4 can select either one vertex at a time for removal, or they can select a maximal set of vertices which can be removed simultaneously without interfering.

In all algorithms, the iterative process may stop either when a given percentage of the available vertices has been inserted / removed, or when the approximation error of the current model reaches a certain global approximation error.

Functionalities 1 and 3 are documented in the paper [vis97].
Functionality 4 is briefly described here.

How to run the program

You can run the program from the command line by typing:

Delaunaymt InFile OutFile [format_string]

where InFile is a file containing:

for algorithms based on vertex insertion (1 and 2), a set of points and, possibly, a set of straight-line segments;
for algorithms based on vertex removal (3 and 4), a possibly constrained Delaunay triangulation.

OutFile will contain the final triangulation resulting from applying the algorithm specified in the format string.

For a description of the format of point and triangulation files, see file formats).

format_string consists of a sequence of options:

opt_algo opt_decim opt_choice opt_error opt_degree opt_stop opt_cdt

which are described in the following.

Avaliable options

opt_algo Mutually exclusive options for choosing the algorithm:

r: Build a Delaunay triangulation through vertex insertions (algorithm 1).
m: Build a constrained Delaunay triangulation through vertex insertions (algorithm 2).
d: Decimate a Delaunay triangulation through vertex removal (algorithm 3).
t: Decimate a constrained Delaunay triangulation through vertex removal (algorithm 4).

opt_decim. Mutually exclusive options for choosing the decimation strategy (for decimation algorithms only, opt_algo = d or t):

n: Remove single vertices one at a time.
s: Remove a maximal set of independent vertices simultaneously.

opt_choice. Mutually exclusive options for selecting the next point to be inserted / removed:

e: Error-driven selection.
r: Random selection.

opt_error. Mutually exclusive options for estimation of the error increase caused by removing a vertex (only for decimation algorithms with error-driven choice of points to be removed, opt_algo = d or t and opt_choice = e):

a: Use a (faster) approximate estimation.
e: Use a (slower) precise estimation.

opt_degree. Mutually exclusive options for the degree of removable vertices (for decimation algorithms only, opt_algo = d or t):

n: Vertices of any degree can be removed.
s maxdegree: Set an upper bound to the degree of a removable vertex (e.g., with s 10 only vertices of degree at most 10 can be removed).

opt_stop. Mutually exclusive options for setting the termination condition:

u number: Stop when the given number of vertices has been inserted or removed (e.g., u 100 inserts / removes 100 vertices). In decimation algorithms, a set of non-removable vertices (the ones defining corners of the domain, the ones with a too high degree w.r.t. a -deg option) will remain in any case.
e norm error: Stop when the approximation error of the current triangulation reaches the given value. Parameter norm specifies how to compute the global error of the triangulation:
- x: maximum error over all triangles;
- s: mean error over all triangles;
- q: mean of squared triangle errors.

opt_cdt. Mutually exclusive options for decimation of constrained triangulations (opt_algo = t):

n: Inform the system that we will use the default parameters.
s: Inform the system that we will redefine the default parameters. In this case, the options is followed by three flags. Each can be set either to s or to n:
1. First flag: if s, enables extension of optimization (slower, but produces triangulations of better quality).
2. Second flag: if s, allows the elimination of points in which exactly one constraint is incident (endpoints of open chains of constraint edges).
3. Third flag: if s, allows breaking closed chains of constraint edges.

By default, all three flags are disabled.

Examples of format strings

d n e a s 10 u 1000
Decimate a triangulation (d) by removing one point at a time (n). The point is chosen on the basis of its approximation error (e) estimated in an approximate way (a). Vertices with a degree larger tham 10 cannot be removed (s 10). The process stops after having removed 1000 vertices (u 1000).
d s r n e x 10.0
Decimate a triangulation (d) by removing sets of independents points simultaneously (s). Points to be removed are chosen randomly (r). No restrictions on the degree of removed vertices (n). The process stops when the approximation error, computed as the maximum error over all triangles, reaches the value 10.0 (e x 10.0).
t n e a s 10 u 1000 n
Decimate a constrained triangulation (t). All settings are as in example 1. In addition, the default settings for CDT decimation are used (n).
t s e e n u 2000 s s s n
Decimate a constrained triangulation (t) by removing sets of independents points simultaneously (s). Points to be removed are chosen according to their error (e) which is computed exactly (e). No limitation on the degree of removable vertices (n). The process stops when 2000 points have been removed (u 2000). The specific settings for CDT decimation are modified (s) in this way: enable extension of optimization and removal of vertices with exactly one incident constraint (s s), do not enable simplification of closed chains of constraints (n).
r r u 1000 Refine a triangulation (r) by inserting points in a random order (r). The process stops after having inserted 1000 points (u 1000).
r e e s 10.0 Refine a triangulation (r) by inserting points chosen on the basis of their approximation error(e). The process stops when the appoximation error of the triangulation, computed as the mean over all triangle errors, reaches the value 10.0 (e s 10.0).
m r u 1000 Refine a constrained triangulation (m) by inserting 1000 points randomly (r u 1000).
Where to find the results
A Multi-Triangulation (file output.mtf) and related tile errors (file output.err) are automatically generated by delaunaymt, provided that the program is compiled with macro MT_TRACER set (as specified in the Makefile).
The algorithm for refining a constrained Delaunay triangulation (opt_algo = m) is not suitable for MT construction. It only exist to provide a way for building a constrained triangulation to be decimated (with opt_algo = t). For this purpose, use the format string m r u num where num is the total number of points in the data file.
File Formats

Input files
The input for vertex-insertion algorithms (algorithms 1 and 2) is an ASCII file made up of a mandatory part containing a set of vertices to be inserted in the triangulation, followed by an optional part containing a set of straight-line segments having their endpoints in the given vertex set.
The syntax for the mandatory part is the following:
```
NumPoints          // Number of points (INTEGER, greater or equal to 3)

X1 Y1 Z1           // First point (three FLOATs)
X2 Y2 Z2           // Second point (three FLOATs)
...
Xn Yn Yn           // Last point (three FLOATs), n = NumPoints
```
The syntax for the optional part is the following:
```
NumSegments        // Number of segments (INTEGER, greater or equal to 0)

I1 J1              // First segment (two INTEGERs)
I2 J2              // Second segment (two INTEGERs)
...
Im Jm              // Last segment (two INTEGERs), m = NumSegments 
```
Integers Ik and Jk are the indices of the two endpoints of the k-th segment in the previous list of vertices; the range of valid indices is [0,NumPoints-1].
The optional part, even if present, is not considered by algorithm 1.
The input for vertex-decimation algorithms (algorithms 3 and 4) is an ASCII file made up of a mandatory part containing a set of vertices and a set of triangles (together forming a triangulation), followed by an optional part containing a set of straight-line segments, subset of the triangulation edges (forming the constraints of a constrained triangulation).
The syntax for the mandatory part is the following:
```
NumPoints          // Number of points (INTEGER, greater or equal to 3)

X1 Y1 Z1           // First point (three FLOATs)
X2 Y2 Z2           // Second point (three FLOATs)
...
Xn Yn Yn           // Last point (three FLOATs), n = NumPoints

NumTriangles       // Number of triangles (INTEGER, greater or equal to 1)

I1 J1 K1           // First triangle (three INTEGERs)
I1 J2 K2           // Second triangle (three INTEGERs)
...
Xt Yt Yt           // Last triangle (three INTEGERs), t = NumTriangles
```
Integers Ik, Jk and Kk are the indices of the three vertices of the k-th triangle in the triangulation. The range of valid indices is [0,NumPoints-1].
The syntax for the optional part is the following:
```
NumSegments        // Number of segments (INTEGER, greater or equal to 0)

I1 J1              // First segment (two INTEGERs)
I2 J2              // Second segment (two INTEGERs)
...
Im Jm              // Last segment (two INTEGERs), m = NumSegments 
```
Integers Ik and Jk are the indices of the two endpoints of the k-th constraint segment in the previous list of vertices; the range of valid indices is [0,NumPoints-1].

Output files
The output for all algorithms is an ASCII file containing a set of vertices and a set of triangles (together forming a triangulation), possibly followed by a set of straight-line segments, subset of the triangulation edges (forming the constraints of a constrained triangulation).
The syntax of such file is the same as that of the input file for vertex-removal algorithms (see description above).
Decimation of a constrained Delaunay triangulation
It is often desirable to maintain certain known lineal features of a terrain (e.g., rivers, ridges, isolines, etc.) in such a way that they are represented at different resolutions in the MT. Algorithm 4 builds a terrain MT that incorporates lineal features at multiple resolutions. This is done by iterative removal of vertices and simplification of the polylines forming the features, in the following way:
- Vertices that are not endpoints of any feature edge are treated as in the standard case.
- Vertices that are endpoints of three or more feature edges are not removed.
- Vertices that are endpoints of exactly two feature edges, if selected for removal, cause the removal of the two feature edges and their replacement with a new feature edge joining the surviving endpoints of the two disappearing feature edges (a polyline is simplified by merging two consecutive segments into one segment).
- Vertices that are endpoints of exactly one feature edge by default cannot be removed. One can enable their removal through a command-line option. In this case, if selected for removal, they cause the removal of the feature edge incident in them (a polyline is shortened).
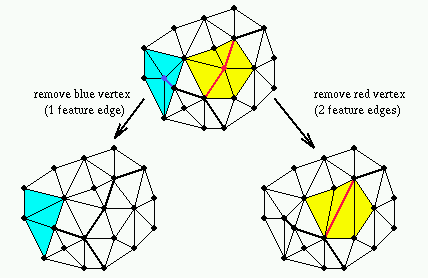
In the current implementation, the horizontal error caused by the approximation of the lineal features with coarser and coarser polylines is not evaluated. In future releases, we plan to evaluate such error and use it for driving the selection of points to be removed.
Conversion utilities
Data for a terrain can be:
- A- a set of scattered points (and segments)
- B- a Triangulated Irregular network
- C- a grid of points
In case A a refinement algorithm (1 or 2) can be applied directly. In order to apply a decimation algorithm (3 or 4) first use a refinement algorithm to build a triangulation containing all the given points (and segments).
In case B a decimation algorithm (3 or 4) can be applied directly. In order to apply a refinement algorithm (1 or 2), just forget the existing triangles and reduce to a set of points.
Case C can be considered as a subcase of A or as a subcase of B, since it is straightforward to abtain a regular triangulation of the grid. A grid file usually contains just the height of the data points. Since Delaunaymt needs the x-y coordinates as well (it assumes to deal with scattered points) a conversion utility is provided. Another conversion utility produces x-y coordinates aa well as the triangles of a regular triangulation of the grid.
The two utility programs are:
- grid2pts.c given a grid, produce a point file
- grid2tri.c given a grid, produce a triangulation file
The resulting files can be processed by program Delaunaymt.

MT DELAUNAY

General Information

How to run the program

Avaliable options

Examples of format strings

Where to find the results

File Formats

Input files

Output files

Decimation of a constrained Delaunay triangulation

Conversion utilities