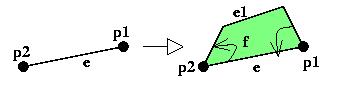Costruzione di mappe da dati GIS

Che cosa e' una mappa

Una mappa M e' costituita da tra insiemi di entita' fra loro correlate: P (punti), L (linee), R (regioni) nel piano.

Una regione e' un sottoinsieme bi-dimensionale del piano; e' delimitata da una o piu' linee chiuse (il contorno esterno ed eventuali contorni di "buchi" interni alla regione); internamente alla regione vi possono essere punti e linee non facenti parte di un contorno, chiamati caratteristiche (o "feature") della regione (feature puntuali e feature lineari); ciascun contorno e ciascuna feature lineare sono formati da linee appartenenti alla mappa; ciascuna feature puntuale e' un punto appartenente alla mappa; tutte le regioni di una mappa hanno estensione finita, tranne la regione esterna infinita.
Una linea e' un sottoinsieme uni-dimensionale del piano; e' una catena di segmenti che puo' essere aperta o chiusa; se la linea e' aperta allora ha due punti estremi, se e' chiusa allora ha un punto estremo (ovvero i due estremi coincidono); gli estremi di una linea sono punti appartenenti alla mappa; una linea e' parte del contorno di al piu' due regioni, oppure e' una feature lineare di esattamente una regione della mappa; i punti di giunzione fra due segmenti consecutivi della catena che costituisce una linea non sono punti della mappa.
Un punto e' un sottoinsieme zero-dimensionale del piano; un punto e' una feature puntuale di una regione, oppure e' un estremo di una o piu' linee della mappa.

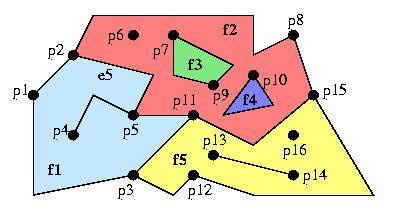Figura: una mappa.
La regione f2 ha un contorno esterno e due contorni interni.
Il punto p6 e' una feature puntuale di f2.
Le regioni f1 e f5 hanno una feature lineare ciascuna.
Il contorno di f2 e' fatto da cinque linee: p2-p8, p8-p15, p15-p11, p5-p11, p2-p5. La regione f3 e' contornata da due linee aperte, f4 da una linea chiusa.

L'intersezione fra due regioni in una mappa puo' solo essere vuota oppure costituita da linee e/o punti appartenenti alla mappa.
L'intersezione fra due linee in una mappa puo' solo essere vuota oppure costituita da punti estremi comuni alle due linee.
Due punti in una mappa devono essere distinti.
Un punto e una linea in una mappa o sono disgiunti oppure il punto e' un estremo della linea.
L'intersezione fra una regione e un'entita' di dimensione minore (linea o punto) in una mappa puo' solo essere vuota oppure coincidente con l'entita' di dimensione minore.

Descrizione di una mappa

Per descrivere una mappa usiamo una struttura dati che memorizza le seguenti informazioni.

Per ogni vertice v:

puntatore a una delle linee che hanno v come estremo
se v e' una feature puntuale, puntatore alla regione che lo contiene

Per ogni linea e:

puntatori ai due punti estremi di e, questo induce un orientamento di e dal primo al secondo estremo (secondo l'ordine in cui sono memorizzati)
puntatori a due tra le linee che condividono con e un punto estremo: la prima linea che si incontra a partire da e ruotando attorno al primo estremo in senso antiorario e la prima linea che si incontra allo stesso modo ruotando attorno al secondo estremo
puntatori alle due regioni che hanno e sul loro contorno: prima quella a sinistra di e e poi quella a destra (considerando e orientato dal primo al secondo estremo)
se e e' una feature lineare, puntatore alla regione che lo contiene

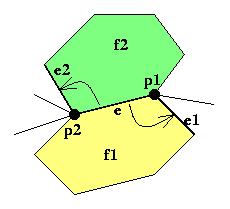Figura: La linea e ha nell'ordine p1,p2 come punti estremi, e1,e2 come linee associate, f1,f2 come facce associate.

Per ogni regione f:

puntatore a una delle linee che formano il contorno esterno di f
per ogni contorno interno, puntatore ad una delle linee che lo formano
per ogni feature puntuale, puntatore al punto
per ogni componente connessa delle feature lineari, puntatore ad una linea fra quelle che formano la componente

Operatori per manipolare mappe

Consideriamo operatori costruttivi (aggiungono entita' ad una mappa collegandole a quelle gia' presenti) e distruttivi (eliminano entita' da una mappa).

Operatori costruttivi:

add_infinity_face(out: f): crea una mappa costituita solo dalla regione esterna infinita.
Parametri: puntatore a una regione f, che verra' inizializzata come regione infinita ed inserita nella mappa.
add_point_feature(inout: f, in: (x,y), out: p): crea un punto e lo aggiunge alla mappa come feature puntuale di una regione esistente.
Parametri: puntatore ad una regione f esistente, che verra' modificata; posizione della feature; puntatore ad un punto p, che verra' inizializzato alla posizione data ed inserito come feature di f.

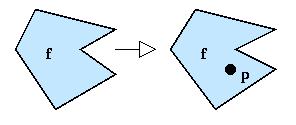Figura: add_point_feature.
f = la regione esistente.
p = il nuovo punto.
add_line_feature(inout: p1, inout: p2, inout: e1, inout: e2, out: e): crea una linea che ha per estremi due punti esistenti e la aggiunge alla mappa come feature lineare di una regione esistente.
Parametri: puntatori a due punti p1,p2 che diventeranno estremi della linea; puntatore a una linea e1 incidente in p1 e puntatore a una linea e2 incidente in p2; puntatore ad una linea e che verra' inizializzata con estremi p1,p2; la linea e verra' inserita nei fasci di linee incidenti in p1,p2 in modo tale che e venga subito dopo e1 girando in senso antiorario attorno a p1 e subito dopo e2 girando in senso antiorario attorno a p2.

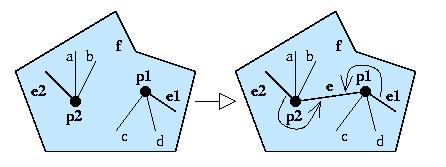Figura: add_line_feature.
f = la regione esistente.
p1,p2 = i due punti esistenti che diventano estremi della nuova linea.
e1,e2 = una linea incidente rispettivamente in p1,p2.
e = la nuova linea.

expand_point_to_line(inout: p, inout: e1, inout: e2, in: (x1,y1), inout: p1, in: (x2,y2), inout: p2, out: e): crea una linea espandendo un punto esistente; elimina il vecchio punto e crea due nuovi punti estremi della linea; il fascio di linee incidenti nel vecchio punto e' diviso in due fasci che vanno a incidere nei due punti estremi della nuova linea.
Parametri: puntatore al punto p da espandere; puntatori a due linee e1,e2 incidenti in p; posizioni dei due estremi della linea da creare; puntatori a due punti p1,p2 che saranno inizializzati con gli estremi della linea; puntatore ad una linea e che sara' inizializzata con la nuova linea di estremi p1,p2; la linea e verra' inserita nei fasci di linee incidenti in p1,p2 in modo tale che e venga subito dopo e1 girando in senso antiorario attorno a p1 e subito dopo e2 girando in senso antiorario attorno a p2.

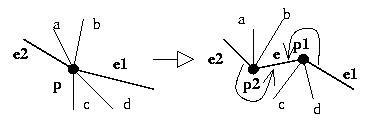Figura: expand_point_to_line.
p = il punto esistente.
e1,e2 = due linee incidenti in p che delimitano dove il fascio di linee incidenti deve essere aperto.
e,p1,p2 = la nuova linea e i due nuovi punti suoi estremi.

expand_point_to_region(inout: p, inout: e1, inout: f1, out: e, out: f): crea una linea chiusa e una regione da essa delimitata espandendo un punto esistente.
Parametri: puntatore al punto p da espandere; puntatore ad una linea e1 incidente in p; puntatore ad una linea e che sara' inizializzata come linea chiusa avente come estremo p; puntatore ad una faccia f che sara' inizializzata come la faccia racchiusa da e; la linea e viene collocata in modo tale da venire subito dopo e1 girando in senso antiorario attorno a p.

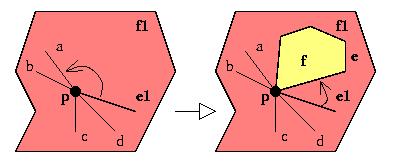Figura: expand_point_to_region.
p = il punto esistente e modificato.
e1 = uno spigolo incidente in p.
f,e = la nuova regione e la nuova linea creata per delimitarla.
expand_line_to_region(inout: e, out: f, out: e1): duplica una linea esistente e crea una regione compresa fra la vecchia e la nuova linea.
Parametri: puntatore alla linea e da duplicare; puntatore ad una linea e1 che sara' inizializzata come una nuova linea avente gli stessi estremi di e ed orientata come e; puntatore ad una regione f che sara' inizializzata come regione delimitata dalle linee e,e1; la regione f verra' creata in modo tale da giacere a sinistra di e e a destra di e1.

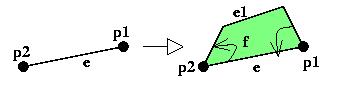Figura: expand_line_to_region.
e = la linea esistente.
f,e1 = la nuova regione, la nuova linea.
split_line(inout: e0, in: (x,y), out: p, out: e2): divide in due una linea esistente creando un punto.
Parametri: puntatore alla linea e da dividere; posizione del punto da inserire su e; puntatore ad un punto p che sara' inizializzato con un nuovo punto situato alla posizione data; puntatore a una linea e1 che sara' inizializzata con uno dei due spezzoni di e, mentre e stessa sara' modificata per diventare l'altro spezzone; e verra' accorciata e restera' fra il suo primo estremo p1 e p, mentre la nuova linea e2 sara' creata fra p e il secondo estremo p2.

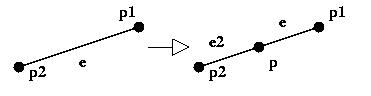Figura: split_line.
e = la linea esistente.
p = il nuovo punto.
e1 = la nuova linea.
split_region(inout: f, inout: p1, inout: p2, out: e, out: f1): divide in due una regione esistente creando una linea che unisce due punti esistenti sul contorno della regione.
Parametri: puntatore alla regione f da dividere; puntatori a due punti p1,p2 sul contorno di f. puntatore a una linea e che sara' inizializzata con estremi p1,p2; puntatore ad una regione f1 che sara' inizializzata con una delle due parti di f, mentre f stessa sara' modificata per diventare l'altra parte; f viene tagliata e resta la parte a sinistra di e, mentre la parte a destra di e diventa una nuova regione f1.

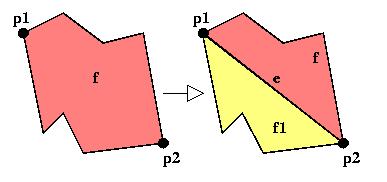Figura: split_region.
f = la regione esistente.
p1,p2 = due punti esistenti sul suo contorno.
e,f1 = la nuova linea e la nuova regione.

Operatori distruttivi (sono gli inversi dei precedenti):

point_abstraction(inout: p): elimina un punto che e' feature puntuale di una regione.
Parametri: puntatore al punto p, feature puntuale, che verra' annullato.
line_abstraction(inout: e): elimina una linea che e' feature lineare di una regione.
Parametri: puntatore alla linea e, feature lineare, che verra' annullato.
line_to_point_contraction(inout: e, in: (x,y), out: p): elimina una linea contraendola in un punto.
Parametri: puntatore alla linea e, che verra' annullata; posizione del nuovo punto; puntatore a un punto p che sara' inizializzato col nuovo punto.
region_to_point_contraction(inout: f): elimina una regione (il cui contorno deve essere costituito da una sola linea) contraendola in un punto.
Parametri: puntatore alla regione f, che verra' annullata. Verra' contratta nell'unico punto che appartiene al suo contorno.
region_to_line_contraction(inout: f, out: e): elimina una regione (il cui contorno deve essere costituito da esattamente due linee) contraendola in una linea.
Parametri: puntatore alla regione f, che verra' annullata; puntatore alla linea; puntatore a un lato che sara' inizializzato con la linea.
line_merge(inout: p, out: e): fonde due linee eliminando il punto estremo comune.
Parametri: puntatore al vertice da eliminare; puntatore a una linea che sara' inizializzaza con il risultato della fusione.
region_merge(inout: e, out: f): fonde due regioni eliminando una linea di contorno comune.
Parametri: puntatore alla linea condivisa dalle due regioni da fondere; puntatore ad una regione che sara' inizializzato con la regione risultante dalla fusione.

I dati disponibili

I dati resi disponibili dal Comune di Genova consistono in spezzate poligonali (aperte o chiuse) e punti isolati.

Assumiamo che i dati soddisfino queste proprieta':

due segmenti non si intersecano ne' all'interno ne' negli estremi, fatta eccezione per due segmenti consecutivi appartenenti alla stessa spezzata, i quali si condividono un estremo comune
un punto (isolato o snodo di spezzata) non coincide con un altro punto ne' giace all'interno di un segmento

Che cosa bisogna fare

Esiste una libreria, chiamata PEG2, che implementa il tipo delle mappe ed una serie di operazioni su mappe tra cui gli operatori costruttivi e distruttivi citati sopra.
La libreria e' implementata sopra CGAL, libreria standard di strutture dati ed algoritmi geometrici.

Bisogna installare e far funzionare CGAL (presupposto per far funzionare PEG2), attualmente l'unica installazione funzionante e' sulla macchina "flash" in Vicolab.

Bisogna scrivere un programma che, presi i dati disponibili, costruisca una mappa. Le operazioni di base per costruirla sono:

inizializzare della mappa (vuota)
aggiungere tutti i punti isolati
aggiungere tutte le spezzate aperte
aggiungere tutte le spezzate chiuse

e sono implementabili a partire da quelle della libreria PEG2 nel modo seguente.

Inizializzazione della mappa

Creare la faccia infinita: add_infinity_face(f).

Aggiunta di un punto isolato

Localizzare la regione R contenente il punto ed inserire il punto come feature puntuale di R.

Parametri: posizione del nuovo punto, puntatore a un punto che lo conterra'.

procedure add_isolated_point(in: (x,y), out: p)
{
  f := point_location(x,y);
  add_point_feature(f,x,y,p);
}

Supponiamo che la funzione point_location restituisca la regione f contenente la posizione assegnata.
Le istruzioni per implementare questa funzione sono sulle dispense del corso di modellazione geometrica, capitolo 4.
Scegliere il metodo senza pre-elaborazione e usare come algoritmo per controllare se un punto sta in una regione l'algoritmo della semiretta.
Le regioni della mappa possono avere buchi, ma l'algoritmo della semiretta e' comunque valido (bisogna considerare tutti i lati, sia del contorno esterno che dei contorni interni della regione).

Aggiunta di una spezzata aperta

Inserire il primo estremo del primo segmento della spezzata come punto isolato (come descritto sopra). Ricordarsi la regione R in cui e' stato inserito (come conseguenza dell'assunzione che i segmenti non si intersechino, questa regione contiene completamente la spezzata).

Poi, per ogni nuovo segmento della spezzata inserire il secondo estremo come punto isolato ed inserire una feature lineare di R congiungente il punto appena inserito con il precedente.

Parametri: posizioni degli N+1 punti della spezzata, puntatore al primo punto p0 della spezzata che sara' inizializzato, a partire da p0 si potranno recuperare tutte le linee e i punti che compongono la catena (e che saranno stati inizializzati anch'essi).

procedure add_open_chain(in: [(x0,y0),...,(xN,yN)], out: p0)
{
  f := point_location(x0,y0);
  add_point_feature(f,x0,y0,p0);
  p := p0;
  e := null;
  for (i=1...N)
  {  add_point_feature(f,xi,yi,p1);
     add_line_feature(p,p1,e,null,e1);
     p := p1;
     e := e1;
  }
}

Aggiunta di una spezzata chiusa

Procedere nello stesso modo descritto per inserire la spezzata chiusa, senza inserire pero' l'ultimo segmento della spezzata (quello che unisce l'ultimo punto della lista al primo).

L'ultimo segmento (quello che chiude la spezzata) divide la regione f (all'interno della quale e' la spezzata) in due regioni, cioe' ritaglia da f una nuova regione f1.

Parametri: posizioni degli N+1 punti della spezzata, puntatore a una regione f1 che sara' inizializzata con la nuova regione creata all'interno della spezzata, a partire da f1 si potranno recuperare le linee e i punti che formano il suo contorno (e che saranno stati inizializzati anch'essi).

procedure add_closed_chain(in: [(x0,y0),...,(xN,yN)], out: f1)
{
  f := point_location(x0,y0);
  add_point_feature(f,x0,y0,p0);
  p := p0;
  e := null;
  for (i=1...N)
  {  add_point_feature(f,xi,yi,p1);
     add_line_feature(p,p1,e,null,e1);
     if (i==1) e0 = e1;
     p := p1;
     e := e1;
  }
  split_region(f,p0,p1,e1,f1);
}