RAPPRESENTAZIONE BINARIA DELL'INFORMAZIONE

In un calcolatore tutta l'informazione è rappresentata in forma binaria, cioè usando solo due simboli, usualmente indicati con le cifre 0 e 1 (in inglese 0 e 1 sono detti bit). Si usa anche il termine digitale, dall'inglese digit (cifra).

La motivazione per limitarsi a due soli simboli è dovuta al fatto che essi possono essere rappresentati convenientemente con dispositivi fisici; per esempio magnetizzato o no, voltaggio alto o basso, luce o buio.

CODIFICA DEI NUMERI

Numeri naturali

Noi rappresentiamo i numeri con una notazione posizionale che utilizza 10 cifre (numeri arabici).
Un numero è rappresentato da una sequenza di cifre, e posizionale significa che il valore di una cifra dipende dalla sua posizione all'interno della sequenza.

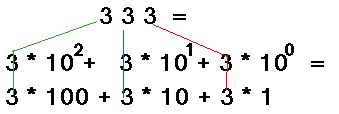
Esistono anche altri tipi di notazione per i numeri ( una breve panoramica); per esempio additive, dove ogni cifra indica una quantità da aggiungere o togliere, come il sistema di numerazione romana.

Inoltre è possibile scegliere in molti modi il numero di cifre differenti che si usano in una notazione posizionale, non solo il 10; in genere si usano anche numerazione in base 2 (binaria), 8 (ottale), 16 (esadecimale).

Numerazione in base p, con p un numero naturale > 1

occorrono p cifre distinte, siano esse C1, ..., Cp (sono semplicemente dei simboli)
un numero è rappresentato da una sequenza di tali cifre.
Sia 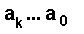una rappresentazione di un numero in base p, esso rappresenta 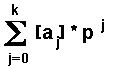, dove 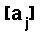rappresenta il numero d'ordine della cifra ([C1] = 0, ..., [Cp] = p-1).

Per la rappresentazione binaria si usano le cifre 0,1; per quella ottale si usano 0,1,2,3,4,5,6,7, e per quella esadecimale si usano 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

Quanti/quali numeri si possono rappresentare usando n cifre binarie ?
Un generico numero binario con n cifre è 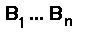Il più piccolo è 0 ... 0 e il più grande è 1 ... 1, che rappresenta 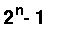; provarlo per induzione aritmetica su n

Come trovare la rappresentazione binaria di un numero naturale

Sia n un numero naturale. La cifra meno significative della rappresentazione binaria di n è data dal resto della divisione di n per 2, e quelle che seguono sono date dai resti delle successive divisioni per due.

Diamo un programma per il calcolatore antropomorfo per eseguire questa trasfomazione 

leggi dall'input il numero da trasformare e scrivilo sul foglietto N

se N = 0 allora scrivi su output cifra 0

mentre N =/= 0 fai
   scrivi resto di N diviso 2 sul foglietto C;
   se C = 0 allora scrivi su output cifra 0
      altrimenti scrivi su output cifra 1;
   scrivi N divisione intera 2 sul foglietto N;
Notare che
ESERCIZI
  1. Scrivere un programma per il calcolatore antropomorfo per trovare il numero naturale rappresentato da un numero binario.
  2. Dare la rappresentazione binaria, ottale, esadecimale del numero naturale 123.
  3. Quale numero naturale rappresenta 123 in base 2, 8 e 16.
  4. È possibile dare una rappresentazione unaria, cioè che usa una sola cifra ?
  5. Definire la rappresentazione in base 5 ed utilizzarla per rappresentare 103.

Numeri interi

Esistono due modi per rappresentare i numeri interi, supponiamo di usare m bit
modulo/segno
il primo bit rappresenta il segno (0 per il + e 1 per il -), i rimanenti n-1 bit rappresentano il modulo (un naturale)
complemento a 2
un numero negativo -N è rappresentato dalla rappresentazione binaria di (2 alla m) - N, quelli positivi come al solito.
Quanti numeri interi si possono rappresentare con m bit
modulo/segno
i numeri compresi tra -((2 alla (m -1)) - 1) e +((2 alla (m -1)) - 1); notare che ci sono due zeri (-0 e +0)
complemento a 2
-2 alla (m-1) e ((2 alla (m-1))-1)
Esempio, usando 4 bit i numeri 5 e -5 sono rappresentati rispettivamente da
modulo/segno
0101 e 1101
complemento a 2
0101 e 1011

Numeri reali

Non è possibile rappresentare tutti i numeri reali utilizzando sequenze finite di bit (problema di cardinalità: l'insieme delle sequenze finite di bit è numerabile, mentre i reali hanno la cardinalità del continuo), pertanto rappresenteremo solo dei numeri razionali.

Rappresentazione in virgola fissa

Si rappresentano la parte intera e quella frazionaria di un numero reale con due sequenze di bit; la pare intera come visto sopra, mentre la parte frazionaria è rappresentata come un numero naturale ma utilizzando esponenti negativi della base (basta notare che, per esempio, 0,34 in base 10 rappresenta (3/10) + (4/100)).
Quindi basta decidere quanti bit usare per la parte intera e quanti per la frazionaria.

Con questa rappresentazione non si riescono a rappresentare molti numeri ed in genere solo numeri piuttosto piccoli; per esercizio quanti/quali numeri si rappresentano con 5+5 bit ?

Rappresentazione in virgola mobile (floating point)

Ricordarsi che nel mondo anglossasone si usa il punto e non la virgola per la parte frazionaria).
Un numero reale può essere visto come

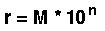
dove M (detta mantissa) è un numero frazionario cioè compreso tra -1 e 1, ed n un numero intero (detto caratteristica)

In questo caso basta decidere quanti bit usare per la mantissa e quanti per la caratteristica.

Con questa rappresentazione si possono rappresentare numeri molto grandi e numeri molto piccoli. Per esercizio qual'è il più piccolo e il più grande numero positivo e negativo rappresentabile usando 5 bit per la mantissa e 3 per la caratteristica ?
In questo caso però i numeri rappresentabili sono distribuiti in modo non uniforme, tanti vicino allo zero e poi sempre meno.

Problemi/conseguenze

Rappresentare i numeri in forma binaria utilizzando un numero fissato di bit porta a varie consequenze e pone dei problemi che occorre aver chiaro quando si scrivono programmi.

Undeflow/Overflow

In ogni calcolatore un numero fissato di bit verrà usato per rappresentare i numeri (siano interi o reali); per esempio per gli interi si usano in genere 32/64 bit.
Effettuando delle operazioni su numeri rappresentati con n bit si può ottenere anche un numero non rappresentabile con tali bit; se il numero è troppo grande si parla di overflow, altrimenti di underflow.

Approsimazione/errore

I numeri reali sono rappresentati come approssimazioni razionali, e quindi modulo un certo errore, ma effettuando delle operazioni su tali numeri l'errore può modificarsi; pertanto occorre tenerne conto per prevedere i possibili effetti.

Per esempio la somma può non essere associativa
(es. (2 alla 32 + 3)+(-3) origina overflow, mentre 2 alla 32 + (3+(-3)) no);
a * (b /a) può essere differente da b;
quantità che dovrebbero essere zero non lo sono e così via.

CODIFICA DEI CARATTERI

I caratteri sono rappresentati con una codifica ad hoc usando un certo numero di bit; sono possibili molte scelte, quelle utilizzate attualmente sono degli standard.

Il più noto è lo standard ASCII che utilizza 7 bit e contiene quindi 128 caratteri, che includono letttere maiuscole e minuscole, cifre, segni di punteggiatura, lo spazio vuoto, detto anche blank, e caratteri di controllo dell'impaginazione, come fine linea, tabulazione, fine pagina.

Tavola dei carateri ASCII completa e versione compatta.

Per un altro set di caratteri più moderno, utilizzato per esempio nelle pagine WEB, vedere ISO LATIN 1.

IMMAGINI, SUONI, VIDEO

Anche altri tipi di informazione possono essere rappresentati come sequenze di bit, pensare al suono digitale dei CD e alla prossima televisione digitale.
L'idea base per rappresentare un'immagine è decomporla in punti, usualmente detti pixel (in origine gli elementi dello schermo), e definire per ogni punto il suo colore (o gradazione di grigio).
Pertanto un'immagine è essenzialmente una matrice i cui elementi descrivono bianco o nero (1 bit per pixel); gradazione di grigio (8 toni 3 bit, 16 toni 4 bit,...), oppure un colore, rappresentato per esempio dicendo quanto rosso, blu e verde contiene (sistema RGB Red, Green and Blu) usando percentuali.
Dato che le immagini possono richiedere un numero enorme di bit per essere rappresentate adeguatamente esistono metodi per compattarle e vi sono anche degli standard, come GIF, TIFF, JPEG, ....

I video sono solo sequenze di immagini opportunamente compattate, mentre per i suoni si usano tecniche basate sulla rappresentazione di un suono come insieme di onde.