Scopo di questo capitolo é di arrivare il più rapidamente possibile alla definizione e comprensione dei circuiti combinatori fondamentali (Multiplexer, Demultiplexer, Sommatori, ALU, ecc.) usati come blocchi costruttivi per la realizzazione di microarchitetture. La comprensione dei circuiti combinatori é anche precondizione essenziale per lo studio dei circuiti sequenziali (registri, memorie, ecc.) usati come blocchi costruttivi per la realizzazione di microarchitetture.
La trattazione parte a livello di definizione di funzioni Booleane, e non richiede particolari prerequisiti per la comprensione oltre ad un minimo di dimestichezza con le notazioni matematica ed algebrica. In particolare non si esaminano i problemi di realizzazione fisica dei dispositivi (se non quelli legati alla risposta nel tempo ed ai ritardi) che richiederebbero nozioni di base di elettronica.
Un'algebra Booleana (dal matematico inglese George Boole) è definita da un insieme A di elementi, da due operazioni binarie + (somma) e · (prodotto) e una unaria ¬ (complementazione) definite su A, da due costanti 0 e 1 che denotano due elementi di A e dai seguenti assiomi:
| somma | prodotto | |
| commutatività | a+b=b+a | a·b=b·a |
| associatività | a+(b+c)=(a+b)+c | a·(b·c)=(a·b)·c |
| assorbimento | a+(a·b)=a | a·(a+b)=a |
| distributività | a+(b·c)=(a+b)·(a+c) | a·(b+c)=(a·b)+(a·c) |
| complemento | a+¬a=1 | a·¬a=0 |
Per ogni elemento a, l'elemento ¬a è detto il complementare di a.
Ogni riga della tabella di sopra contiene due assiomi: uno per la somma e uno corrispondente per il prodotto. Notare come sia possibile passare da un assioma all'altro in una stessa riga scambiando tra loro ogni simbolo di somma e di prodotto e ogni simbolo 0 e 1. Vale infatti la proprietà di dualità: ogni legge (ossia, ogni uguaglianza derivabile dagli assiomi) ha una legge duale, ottenuta con lo scambio +/· e 0/1. Più in generale, ogni proprietà ha una corrispondente proprietà duale.
Tuttavia è importante notare che in generale una formula non è equivalente alla sua forma duale: per esempio a+1 è sicuramente diverso da a·0! Infatti la valutazione delle due formule produce valori diversi per qualsiasi valore di a.
In virtù dell'associatività di somma e prodotto, possiamo omettere parentesi inutili e scrivere, per esempio, a+b+c invece di (a+b)+c o a+(b+c).
Come al solito si possono risparmiare ulteriori parentesi inutili definendo delle regole di precedenza tra gli operatori. Convenzionalmente l'operatore ¬ ha precedenza sull'operatore · che, a sua volta, ha precedenza sull'operatore +. Quindi, la formula ¬a+b·c è equivalente a (¬a)+(b·c).
La seguente tabella contiene una serie di leggi (e corrispondente duale) derivabili dagli assiomi.
| somma | prodotto | |
| elemento neutro | a+0=a | a·1=a |
| elemento nullo | a+1=1 | a·0=0 |
| idempotenza | a+a=a | a·a=a |
| involuzione | ¬¬a=a | ¬¬a=a |
| complementazione | ¬0=1 | ¬1=0 |
| De Morgan | ¬(a+b)=¬a·¬b | ¬(a·b)=¬a+¬b |
| espansione | a+b=a+¬a·b | a·b=a·(¬a+b) |
L'insieme di queste leggi ci permette di sostituire delle formule complesse con altre formule equivalenti più semplici (e quindi meglio comprensibili e maneggiabili). Tecniche di semplificazione delle formule booleane assumono una particolare rilevanza quando si affronta il problema della realizzazione di circuiti combinatori.
Esistono infinite algebre booleane non isomorfe; tra tutte, quelle che ci interessano maggiormente sono le algebre dove
Tra tutte le possibili scelte di U, consideriamo quelle dove U ha cardinalità 1. In questo caso gli elementi dell'algebra sono solo 2: l'insieme vuoto (corrispondente alla costante 0) e l'insieme U (corrispondente alla costante 1).
Visto che esistono due soli elementi che corrispondono alle costanti 0 e 1, le operazioni +, · e ¬ sono totalmente definite dalle seguenti tabelle:
|
|
|
A questo punto la corrispondenza con la logica proposizionale dovrebbe essere lampante: + è l'operatore booleano or (detto anche disgiunzione logica), · è l'operatore booleano and (detto anche congiunzione logica), ¬ è l'operatore booleano not (detto anche negazione logica), 0 è e 1 sono rispettivamente i due valori booleani (o di verità) false e true.
Per essere in grado di progettare circuiti combinatori, dobbiamo prima definire cosa sono.
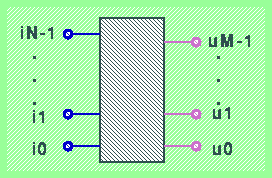
Astrattamente, possiamo definire un circuito combinatorio come una scatola nera (ossia una scatola di cui non conosciamo il contenuto, ma di cui possiamo solo osservare le interazioni con l'ambiente in cui viene posta) composta da N ingressi ed M uscite:

Ogni ingresso e ogni uscita può assumere uno dei due valori booleani 0 e 1. Più precisamente, i valori di una qualunque uscita variano esclusivamente in funzione dei valori assunti dagli N ingressi. Ciò significa che il comportamento di ogni circuito combinatorio con N ingressi ed M uscite può essere specificato da una funzione booleana
f:{0,1}N --> {0,1}M
che a ogni successione di N valori booleani iN-1,...,i0 associa una successione di M valori booleani uM-1,...,u0=f(iN-1,...,i0).
Quindi, per specificare il comportamento astratto di un circuito combinatorio bisogna trovare un modo conveniente per rappresentare una qualsiasi funzione booleana. Due possibili rappresentazioni sono le tavole di verità e le formule booleane. Successivamente introdurremo anche le mappe di Karnaugh, una rappresentazione basata anch'essa su tavole, che permette però di passare facilmente a formule booleane minimali.
In pratica, i circuiti combinatori di una certa complessità vengono realizzati assemblando assieme dei circuiti elettronici molto più semplici detti porte logiche elementari; essi realizzano le funzioni booleane più semplici e sono i mattoni di base che permettono la costruzione di tutti gli altri circuiti più complessi.
Oltre alle tre operazioni or, and e not, le porte logiche realizzano anche le operazioni booleane chiamate xor (or esclusivo), nor, nand e xnor. Valgono le seguenti identità
| xor(a,b)=¬a·b+a·¬b |
| nor(a,b)=¬(a+b)=¬a·¬b |
| nand(a,b)=¬(a·b)=¬a+¬b |
| xnor(a,b)=¬xor(a,b)=a·b+¬a·¬b |
dalle quali si ricavano le seguenti tavole di verità.
|
|
|
|
Notare che xor e xnor realizzano rispettivamente il controllo di disuguaglianza e uguaglianza tra due bit.
A ogni tipo di porta logica è associata una rappresentazione grafica, che è indipendente dalla sottostante realizzazione elettronica.
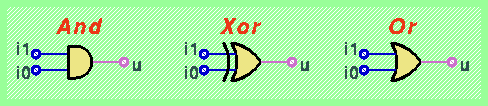

In generale, per rappresentare la porta not in modo più compatto, si usa la regola di aggiungere un "pallino" alla connessione di un filo di ingresso oppure di uscita al simbolo che rappresenta una data funzione logica.
Per ogni tipo di porta logica elementare a due ingressi esistono anche le versioni a più di due ingressi; le definizioni di tali estensioni sono ovvie per gli operatori che sono associativi, ossia or, and, xor e xnor. Per gli operatori non associativi nor e nand la definizione è comunque quella intuitiva: nor(aN-1,...,a0)=¬(aN-1+...+a0) e nand(aN-1,...,a0)=¬(aN-1·...·a0).
Per esempio, la porta logica and a quattro ingressi può essere definita come combinazione di tre porte and a due ingressi. Tale composizione viene rappresentata graficamente come in figura:
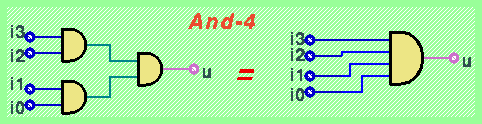
Analoga estensione viene fatta per le altre porte logiche elementari a due ingressi.
In particolare, si può dimostrare per induzione su N che una porta xor a N ingressi restituisce 1 se c'è un numero dispari di ingressi a 1, 0 altrimenti. Quindi una porta xor a N ingressi permette di calcolare il valore del bit di parità per N bit di dato. Dualmente, una porta xnor a N ingressi restituisce 0 se c'è un numero dispari di ingressi a 1, 1 altrimenti.
Costituiscono la rappresentazione di riferimento concettuale per la definizione delle funzioni booleane.
Per esempio, la seguente tavola
| i2 i1 i0 | u1 u0 |
| 000 | 01 |
| 001 | 10 |
| 010 | 11 |
| 011 | 00 |
| 100 | 10 |
| 101 | 10 |
| 110 | 01 |
| 111 | 01 |
rappresenta la funzione f:{0,1}3 --> {0,1}2 tale che f(000)=01, f(001)=10, f(010)=11, f(011)=00, f(100)=10, f(101)=10, f(110)=01, f(111)=01
Nelle righe delle tavole di verità le configurazioni di ingresso sono sempre ordinate in modo che le loro decodifiche in numeri naturali siano crescenti (000, 001, 010, ...).
Dal punto di vista pratico, l'uso é limitato al caso di poche variabili di ingresso (max 5 o 6) a causa della crescita esponenziale del numero di righe. Infatti, una funzione booleana ad N ingressi è rappresentabile da una tavola di verità con 2N righe. Quindi, al crescere del numero delle variabili, il metodo di rappresentazione mediante le tavole di verità diventa impraticabile (a causa delle dimensioni delle tabelle), per cui si preferisce far ricorso a tecniche algebriche per il trattamento manuale. Per il trattamento automatico (mediante strumenti software di supporto) si fa invece uso di strutture dati per la rappresentazione di funzioni chiamate Binary Decision Diagrams (BDD) (non trattati in questo corso).
Chiamiamo letterale una formula costituita da una sola variabile o dalla negazione di una variabile proposizionale
Una formula booleana viene detta in forma normale disgiuntiva quando é formata da una somma di prodotti di letterali.
Analogamente, una formula booleana viene detta in forma normale congiuntiva quando é formata da un prodotto di somme di letterali.
Per riuscire a trattare correttamente i casi limite, introduciamo le seguenti definizioni:Una formula in forma normale disgiuntiva (congiuntiva) viene detta minimale quando, applicando le proprietà delle leggi algebriche booleane, non è possibile ottenere una formula normale disgiuntiva (congiuntiva) equivalente contenente un numero inferiore di letterali.
Illustriamo prima un semplice algoritmo per ricavare da una tavola di verità la corrispondente formula in forma normale disgiuntiva
Data una tavola di verità scandire tutte le righe partendo dalla prima.
Per ogni riga, osservare il valore specificato per l'uscita: se é 0, allora passare alla riga seguente senza far nulla; se invece il valore specificato é 1, allora scrivere un termine da aggiungere ai termini gia scritti in precedenza composto dal prodotto di tutte le variabili di ingresso che assumono il valore 1 e della negazione di tutte le variabili di ingresso che assumono il valore 0. Notare che se l'uscita vale sempre 0 per ogni configurazione in ingresso, allora l'algoritmo restituisce la somma di zero prodotti che corrisponde in effetti alla formula 0.
Siccome ogni funzione boolena è rappresentabile tramite tavola di verità, questa traduzione ci permette di rappresentare ogni funzione boolena è con una formula in forma normale disgiuntiva.
Esempio: considerare la seguente tavola di verità che definisce una funzione di 3 variabili di ingresso
i0 i1 i2 | u ---------+-- 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 0 1 1 | 1 1 0 0 | 1 1 0 1 | 0 1 1 0 | 1 1 1 1 | 1
L'algoritmo di traduzione produce quindi la somma di 4 termini (corrispondenti alle righe 4, 5, 7 e 8 della tavola):
u = ((¬i0)·i1·i2) + (i0·(¬i1)·(¬i2)) + (i0·i1·(¬i2)) + (i0·i1·i2)
A questa formula corrisponde il seguente circuito combinatorio:
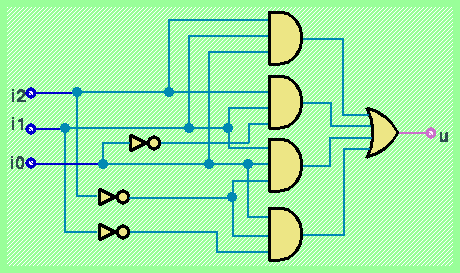
Notare che tale formula normale non é minimale. Per esempio, applicando alcune delle proprietà algebriche di trasformazione delle formule é possibile riscrivere la stessa funzione nella forma normale (più compatta):
u = (i1·i2) + (i0·(¬i2))
Tale formula non é ulteriormente trasformabile in un'altra formula normale disgiuntiva più semplice, quindi viene detta forma normale disgiuntiva minimale per la funzione considerata. Il corrispondente circuito risulta semplificato di conseguenza:

Esistono algoritmi per la costruzione della forma minimale, ma noi non ci soffermeremo su questo aspetto (ormai obsoleto a causa dell'uso di strumenti software per la rappresentazione di funzioni booleane).
Applicando il principio di dualità all'algoritmo di traduzione da tavola di verità a formula in forma normale disgiuntiva, si può definire un algoritmo per la traduzione in formule in forma normale congiuntiva. L'algoritmo duale è il seguente:
Data una tavola di verità in forma canonica, scandire tutte le righe partendo dalla prima.
Per ogni riga, osservare il valore specificato per l'uscita: se é 1, allora passare alla riga seguente senza far nulla; se invece il valore specificato é 0, allora scrivere un termine da moltiplicare per i termini già scritti in precedenza composto dalla somma di tutte le variabili di ingresso che assumono il valore 0 e della negazione di tutte le variabili di ingresso che assumono il valore 1. Notare che se l'uscita vale sempre 1 per ogni configurazione in ingresso, allora l'algoritmo restituisce il prodotto di zero somme che corrisponde in effetti alla formula 1.
Questa traduzione duale ci permette di concludere che ogni funzione boolena è rappresentabile tramite una formula in forma normale sia disgiuntiva che congiuntiva.
Le formule booleane in forma normale (disgiuntiva o congiuntiva) hanno diversi vantaggi rispetto alle tavole di verità:
In generale, una funzione booleana viene rappresentata in modo più sintetico mediante una formula booleana in forma normale, visto che è possibile semplificare la formula, mediante le leggi delle algebre booleane, in modo da ridurla in una forma minimale equivalente.
Dalla struttura di una formula booleana si ricava facilmente la struttura del circuito corrispondente che verrà realizzato tramite opportuna composizione di porte logiche elementari. Inoltre gli algoritmi di traduzione da tavole di verità a forme normali dimostrano che ogni circuito combinatorio può essere ottenuto mediante composizione delle sole porte logiche elementari OR, AND e NOT.
Diciamo che un circuito è realizzato in logica a N livelli se N è il numero massimo di porte logiche che si incontrano seguendo un qualsiasi percorso da uno degli ingressi a una delle uscite del circuito.
Le formule booleane in forma normale permettono di realizzare circuiti in logica a N livelli, con N <= 3. Come vedremo in seguito, questa caratteristica è importante per garantire che i circuiti abbiano ritardi di risposta ridotti.
Visto che il passaggio da formula booleana al corrispondente circuito è abbastanza intuitiva, non entreremo nei dettagli della formalizzazione. Ci limitiamo a osservare che durante tale trasformazione è possibile applicare due tipi di semplificazione: una per ridurre il numero di porte logiche utilizzate, l'altra per ridurre il numero di livelli della logica. Per esempio, la formula ¬a·b+¬a·c si traduce in un circuito che contiene 1 OR a 2 ingressi, 2 AND a 2 ingressi e 1 (e non 2!) NOT. Analogamente, se si vuole realizzare un circuito corrispondente alla formula i0+i1+i2+i3+i4+i5+i6+i7 usando solo OR a 2 ingressi, lo si può fare usando 7 OR e una logica a 3 (e non 7!) livelli.
Abbiamo visto che ogni funzione booleana può essere espressa da una formula in forma normale, quindi ogni circuito combinatorio può essere realizzato usando solo tre tipi di porte logiche: OR, AND e NOT.
Possiamo ulteriormente diminuire i tipi di porte limitandoci a solo NOR o a soli NAND. Infatti, le seguenti identità mostrano come OR, AND e NOT possano essere espressi mediante soli NOR o soli NAND:
| ¬a=¬(a+a)=a NOR a | ¬a=¬(a·a)=a NAND a |
| a+b=¬¬(a+b)=¬(a NOR b)=(a NOR b) NOR (a NOR b) | a·b=¬¬(a·b)=¬(a NAND b)=(a NAND b) NAND (a NAND b) |
| a·b=¬(¬a+¬b)=¬a NOR ¬b=(a NOR a) NOR (b NOR b) | a+b=¬(¬a·¬b)=¬a NAND ¬b=(a NAND a) NAND (b NAND b) |
È importante notare che se applichiamo la trasformazione a una formula
in forma normale rimaniamo in una logica a non più di 3 livelli.
Per esempio,
¬a·b+¬c·¬d=¬(¬a·b)NAND¬(¬c·¬d)=(¬a
NAND b)NAND(¬c NAND ¬d)=((a NAND a) NAND b)NAND((c NAND c) NAND
(d NAND d))
Per il principio di dualità otteniamo lo stesso risultato se
trasformiamo una formula in forma normale
congiuntiva in una con soli NOR.
Per questo motivo le porte logiche NOR e NAND vengono dette universali. Questa considerazione ha un impatto profondo e positivo sulla realizzazione dei circuiti combinatori. Noi non ci occuperemo qui di studiare come una porta logica elementare possa essere realizzata in pratica, ma ci limitiamo a sottolineare l'importanza che può avere dal punto di vista della semplicità e dell'economia di realizzazione dei dispositivi il fatto di potersi sempre ricondurre ad un unico componente universale (NOR oppure NAND).
Sempre dal punto di vista realizzativo, occorre poi notare che la tecnologia elettronica permette di realizzare NOR o NAND con numero di ingressi anche molto elevato praticamente nello stesso modo e con le stesse caratteristiche delle porte a due soli ingressi. Ciò rende particolarmente appetibile la forma di realizzazione in logica a 3 livelli derivante dalla specifica di una funzione in forma normale disgiuntiva (o congiuntiva). Infatti, la realizzazione fisica dei dispositivi induce comunque dei ritardi nel calcolo delle funzioni a seguito di variazioni dei valori in ingresso. Nel caso di realizzazione in logica a 3 livelli, il ritardo massimo per ottenere il risultato corretto in uscita dopo aver cambiato i valori di ingresso sarà comunque pari a tre volte il ritardo del componente universale NOR o NAND, indipendentemente dalla complessità della funzione e dal numero di variabili in ingresso.
L'algoritmo consiste nell'elencare tutte le configurazioni possibili in ingresso (in ordine crescente di valore, quando l'insieme degli ingressi viene interpretato come codifica binaria di numeri naturali). Per ogni configurazione di ingresso, valutare i valori di uscita delle funzioni elementari Not, And e Or che compongono l'espressione. L'uscita della funzione Or rappresenta il valore da inserire nella corrispondente riga della tavola di verità che si sta costruendo.
Con questo abbiamo dimostrato la perfetta equivalenza tra queste due forme di rappresentazione (in quanto ciascuna può essere tradotta automaticamente nell'altra, e viceversa.
Furono originariamente introdotte come rappresentazione alternativa alla tavola di verità per supportare meglio un algoritmo di traduzione in formula normale disgiuntiva minimale. Noi non ci soffermeremo molto sull'uso delle mappe per l'identificazione di tale forma minimale, ma ci limiteremo prevalentemente ad utilizzarle come rappresentazione alternativa più compatta della tavola di verità.
L'idea base consiste nell'usare uno spazio bidimensionale per la rappresentazione delle configurazioni di ingresso, anziché monodimensionale come nel caso della tavola di verità. L'insieme delle variabili di ingresso viene partizionato in due sottoinsiemi (di dimensioni il più possibile bilanciate). Un sottoinsieme viene usato per definire una coordinata orizzontale mentre l'altro insieme viene usato per definire una coordinata verticale. La coppia di coordinate individua una casella nella quale viene scritto il valore di uscita della funzione.
Esempio: la mappa di Karnaugh equivalente alla tavola di verità della funzione usata in precedenza risulta essere:
\ i2 | 0 : 1 |In questo caso abbiamo scelto la coppia di ingressi i0 e i1 per comporre la coordinata verticale (che identifica una riga tra 4) e l'ingresso i2 per determinare la coordinata orizzontale (che identifica una colonna tra 2).
i0 i1 \ | : |
--------\--+-----:-----+
0 0 | 0 : 0 |
..........|.....:.....|
0 1 | 0 : 1 |
..........|.....:.....|
1 0 | 1 : 0 |
..........|.....:.....|
1 1 | 1 : 1 |
-----------+-----:-----+
Nel caso si voglia utilizzare la rappresentazione per ricavare una formula algebrica minimale, normalmente si fa ricorso ad un ordinamento delle combinazioni di valori per le variabili di ingresso diverso dall'ordine lessicografico usato per convenzione nelle Tavole di Verità. Risulta infatti piu' conveniente un ordinamento secondo il cosiddetto "Codice Gray", che é caratterizzato dalla proprietà di avere sempre distanza di Hamming unitaria tra codifiche adiacenti. Nel nostro esempio l'uso dell'ordinamento secondo il codice Gray ci porterebbe a scrivere la tabella come:
\ i2 | 0 : 1 |Questa proprietà permette di stabilire una relazione diretta tra l'adiacenza "grafica" delle caselle della mappa e l'adiacenza in termini di distanza di Hamming tra le combinazioni di valori in ingresso. In particolare, possiamo notare che tutte le caselle contenenti "1" sono adiacenti a due a due: questo significa che se prendiamo le loro coordinate booleane, queste avranno distanza di Hamming unitaria, ossia differiranno per un solo bit. Tale proprietà ci permette di identificare delle coppie di caselle adiacenti contenenti lo stesso valore (1 in questo caso) semplicemente omettendo la coordinata che assume valore diverso nella coppia. Per esempio, invece di considerare separatamente le due caselle in basso nella colonna a sinistra (quella caratterizzata da i2=0), esse hanno in comune la coordinata i0=1, mentre differiscono per il valore di i1; possiamo quindi identificare l'insieme di queste due caselle mediante l'espressione:
i0 i1 \ | : |
--------\--+-----:-----+
0 0 | 0 : 0 |
..........|.....:.....|
0 1 | 0 : 1 |
..........|.....:.....|
1 1 | 1 : 1 |
..........|.....:.....|
1 0 | 1 : 0 |
-----------+-----:-----+
In modo analogo possiamo individuare l'insieme delle due
caselle centrali
della colonna a destra (anch'esse caratterizzate dal valore "1")
mediante
l'espressione:
i1·i2.
L'unione di questi due insiemi di due caselle copre
completamente tutte e sole le caselle della mappa caratterizzate dal
valore "1", quindi possiamo ritrovare la formula normale disgiuntiva
minimale della nostra funzione sommando (logicamente, ossia calcolando
la funzione OR tra) le coordinate di questi due insiemi di caselle:
(i0·(¬i2))+(i1·i2).
Vediamo ora i più comuni circuiti per la codifica, decodifica e commutazione di informazioni rappresentate sotto forma binaria. Tali circuiti costituiscono gli elementi costruttivi per la definizione di sistemi più complessi. Faremo riferimento alle tavole di verità per la definizione di questi circuiti, ma poi li tratteremo come unità funzionali più complesse, il cui funzionamento si intende noto senza ulteriori specificazioni a livello di tavole di verità.
L'esempio di funzione a tre ingressi e una uscita visto in precedenza é un multiplexer ad 1 bit con due ingressi dati (i0 e i1) ed un segnale di controllo (ingresso i2). Come si può facilmente notare dalla mappa che ne descrive il funzionamento, i2=0 implica u=i0, mentre i2=1 implica u=i1. Il valore dell'ingresso di controllo i2 consente quindi di riportare in uscita al multiplexer uno dei due valori in ingresso (i0 oppure i1).
L'idea di circuito multiplexer può essere estesa in diversi modi. Per esempio si può mantenere un solo ingresso di controllo, ma commutare uno tra due insiemi di variabili di ingresso su un solo insieme di variabili di uscita (ogni insieme di variabili di ingresso deve avere la stessa cardinalità dell'insieme di variabili di uscita. In figura é rappresentato lo schema realizzativo di un multiplexer operante su due insiemi di ingresso, ciascuno composto da tre variabili booleane.
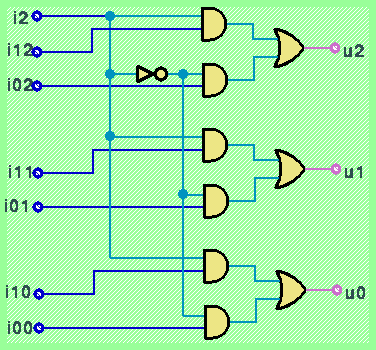
La simbologia usata per la rappresentazione di un multiplexer a prescindere dalla sua realizzazione in termini di porte logiche elementari é la seguente:

Un secondo tipo di estensione del circuito multiplexer viene ottenuto utilizzando una codifica binaria su più bit per la scelta tra più di due ingressi da connettere sull'unica uscita. In figura é illustrato il caso di un multiplexer a 4 ingressi (ciascuno da un bit) comandato da due segnali di controllo in ingresso:
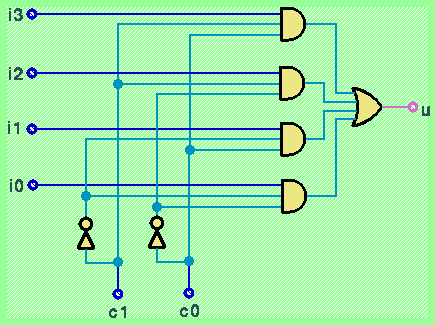
La combinazione degli ingressi c1 e c0 determina la scelta dell'ingresso (per esempio c1=1 e c0=1 "sceglie" i3) da connettere all'uscita u. Notare che in tal caso il numero di ingressi di controllo deve essere pari al logaritmo in base 2 del numero di ingressi che possono essere scelti per la connessione con l'uscita.
Ovviamente i due tipi di estensione del multiplexer (commutazione di più bit e scelta tra più di due ingressi) possono essere combinati in modo da formare, per esempio un multiplexer con 8 insiemi di ingresso, ciascuno da 32 bit, comandato attraverso la codifica su 3 ingressi di controllo.
Un circuito demultiplexer viene definito come l'inverso di un circuito multiplexer, ossia come un elemento funzionale capace di commutare un solo ingresso su due o più uscite. Per convenzione, le uscite "non attivate" assumono il valore costante 0, indipendentemente dal valore assunto dall'ingresso "dati". Notare che questa convenzione pone un vincolo sui codici che possono essere utilizzati per trattare le informazioni in uscita da un demultiplexer: il valore 0 deve poter essere interpretato come un valore non significativo, una condizione di riposo, ecc., in quanto questo valore viene assegnato a tutte le uscite non connesse con l'ingresso.
In figura é riportato un esempio di realizzazione di un demultiplexer a 2 uscite (comandato da un segnale di controllo c) in grado di commutare informazioni codificate su due bit.
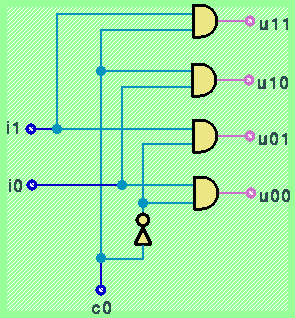
La rappresentazione "astratta" di un tale dispositivo (prescindendo dalla sua realizzazione in termini di funzioni And e Not) é la seguente:
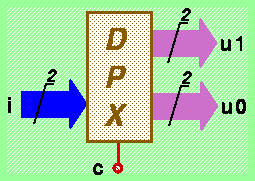
Circuiti demultiplexer possono essere realizzati con numero arbitrario di bit di ingresso e uscita, e con numero di ingressi di controllo pari al logaritmo in base 2 del numero di gruppi di uscite. La codifica binaria dei segnali di controllo individua univocamente l'insieme delle uscite attive che possono riprodurre inalterata la configurazione sull'insieme degli ingressi dati. Le altre uscite (quelle non corrispondenti al codice binario selezionato mediante gli ingressi di controllo) assumono il valore costante 0.
Circuiti di tipo multiplexer e demultiplexer hanno in comune tra loro una parte per la decodifica delle configurazioni booleane di controllo. Tale parte viene normalmente chiamata decoder. Un circuito di tipo decoder può essere pensato come un caso particolare di circuito demultiplexer, nel quale il segnale da commutare su una sola delle uscite é la costante 1. In figura é riportato a titolo di esempio lo schema di realizzazione di un decoder binario da 3 bit.
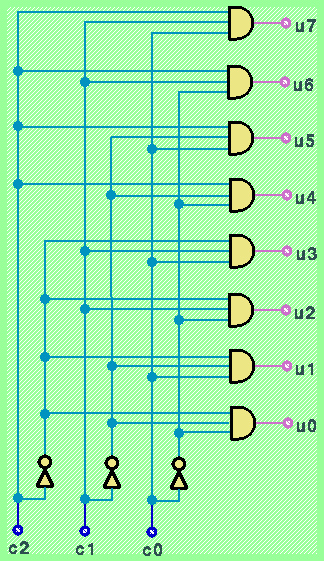
Circuiti di tipo decoder vengono normalmente utilizzati come componenti per la realizzazione di meccanismi di indirizzamento binario. Le uscite possono essere usate per abilitare il funzionamento di moduli simili l'uno all'altro, individuati tramite un indirizzo binario.
Notare che le uscite di un decoder possono essere messe in
corrispondenza
con le righe di una tavola di verità per un circuito combinatorio
con numero di ingressi pari al numero di bit di controllo del decoder.
Per esempio, le 8 uscite del decoder riportato in figura possono essere
messe in corrispondenza con le 8 righe della tavola di verità
di un qualsiasi circuito combinatorio con 3 variabili di ingresso.
Unendo con una funzione Or tutte e sole le uscite del decoder
corrispondenti
a quelle righe della tavola di verità contenenti il valore 1,
é quindi possibile realizzare in modo sistematico qualsiasi tavola
di verità.
Passiamo ora a vedere come, grazie all'uso di tecniche di codifica binaria, possiamo definire dei circuiti booleani in grado di effettuare delle manipolazioni di tipo numerico su rappresentazioni di numeri. In generale il metodo consiste nel definire un algoritmo di manipolazione su rappresentazioni binarie finite. La definizione viene data sotto forma esaustiva mediante la definizione della tavola di verità. La correttezza della realizzazione dipende dall'uso della tecnica di codifica assunta per la progettazione del circuito.
Cominciamo a considerare il caso semplice di rappresentazioni binarie di numeri su un solo bit (ossia numeri interi compresi tra 0 e 1). Notiamo subito che la somma dei valori 1+1=2 genera un valore di uscita non rappresentabile in forma binaria su un bit; per consentire la rappresentazione del risultato occorre infatti che il risultato venga rappresentato con almeno un bit in più rispetto al numero di bit usati per la rappresentazione degli addendi (in modo da poter codificare un valore massimo almeno doppio rispetto al massimo valore dei due addendi). La tavola di verità che specifica il comportamento di un tale circuito addizionatore é quindi la seguente:
s1: a b | u1 u0Possiamo notare che la colonna u0 corrisponde alla tavola di verità della funzione XOR, mentre la colonna u1 corrisponde a quella della funzione AND. Le due uscite del circuito possono quindi essere ottenute mediante l'uso di queste due funzioni elementari applicate alla stessa coppia di ingressi a e b. Un tale circuito con due ingressi e due uscite viene normalmente chiamato half adder (semi addizionatore), per il motivo che scopriremo tra poco.
------+------
0 0 | 0 0
0 1 | 0 1
1 0 | 0 1
1 1 | 1 0
Passiamo ora al caso di somma tra due numeri rappresentati su 2 bit (con risultato rappresentato su 3 bit). Il funzionamento del circuito, usando la normale codifica binaria, può essere definito mediante la seguente mappa:
\ b1 | 0 : 0 : 1 : 1 |
\ b0 | 0 : 1 : 0 : 1 |
a1 a0 \ | : : : |
--------\--+-----:-----:-----:-----+
0 0 | 000 : 001 : 010 : 011 |
..........|.....:.....:.....:.....|
0 1 | 001 : 010 : 011 : 100 |
..........|.....:.....:.....:.....|
1 0 | 010 : 011 : 100 : 101 |
..........|.....:.....:.....:.....|
1 1 | 011 : 100 : 101 : 110 |
-----------+-----:-----:-----:-----+
La realizzazione diretta di tale circuito risulta evidentemente molto più complessa di quella di un semi addizionatore. In oltre, la complessità di realizzazione diventa rapidamente proibitiva se aumentiamo ulteriormente il numero di bit di rappresentazione per gli addendi e per il risultato.
La soluzione che consente di realizzare in modo semplice ed efficiente circuiti addizionatori per rappresentazioni su due o più bit consiste nel modularizzare la realizzazione.
In questo caso la corretta modularizzazione può essere individuata facendo ricorso all'algoritmo di somma cifra per cifra: ad ogni passo consideriamo una sola cifra dell'addendo a e una sola cifra dell'addendo b, oltre all'eventuale cifra "di riporto" derivante dall'applicazione dello stesso algoritmo alle cifre precedenti. Quindi ad ogni passo operiamo su rappresentazioni binarie di un solo bit; l'unica differenza rispetto al circuito semi sommatore visto in precedenza é che ora dobbiamo considerare la presenza di 3 addendi da un bit (a, b e la cifra di riporto c).
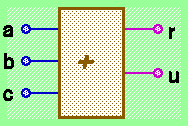
La specifica di un circuito in grado di effettuare tale somma (chiamato full adder, o sommatore completo a 1 bit) é data dalla seguente tavola di verità:
s2: a b c | r uL'uscita u corrisponde ad una funzione XOR a tre ingressi, mentre l'uscita r deve essere generata da un circuito in grado di riconoscere la condizione "almeno due ingressi assumono il valore 1". Indichiamo in modo compatto un circuito di tipo full-adder mediante il seguente simbolo:
---------+------
0 0 0 | 0 0
0 0 1 | 0 1
0 1 0 | 0 1
0 1 1 | 1 0
1 0 0 | 0 1
1 0 1 | 1 0
1 1 0 | 1 0
1 1 1 | 1 1
Tali moduli possono essere combinati in modo da realizzare l'operazione di somma tra rappresentazioni binarie su più cifre, usando un modulo per ogni cifra; ciascun modulo genera una cifra di "riporto" verso il modulo successivo. In figura viene riportato lo schema di connessione di due moduli per formare un addizionatore per addendi rappresentati su due bit (e risultato rappresentato su 3 bit).
Questo problema in pratica viene risolto con l'aggiunta di ulteriori
circuiti
combinatori realizzati in logica a 3 livelli per la "previsione delle
cifre di riporto" (carry lookahead).
Per esempio, la cifra binaria più a sinistra nelle caselle della
mappa del circuito sommatore a
2 bit
può essere usata per specificare un
circuito di previsione del riporto sulla terza cifra.
Una possibile realizzazione della funzione di previsione del
riporto sulla terza cifra in logica a due livelli (nessuna variabile
appare in forma negata in questo esempio) potrebbe quindi essere
definita dalla formula (normale disgiuntiva):
(a1·b1)+(a0·a1·b0)+(a0·b1·b0).
Notiamo infine che un circuito sommatore su N bit progettato per operare su rappresentazioni binarie di numeri senza segno può essere usato anche per operare su rappresentazioni di numeri con segno in complemento a 2 su N bit. L'unica accortezza che occorre osservare in tal caso é quella di definire il risultato su N bit (senza considerare l'N+1-esimo bit di riporto), e quindi di accertarsi che il risultato di una operazione di somma tra numeri dello stesso segno non generi condizioni di overflow.
Un caso particolare di dispositivo sommatore é costituito dal caso
di un "incrementatore" che somma un valore costante K ad un addendo
variabile A.
Nella maggior parte dei casi ci si riduce a voler sommare la costante
K=1
ad un valore arbitrario in ingresso.
In tal caso il dispositivo può essere realizzato in modo molto semplice
usando N moduli di tipo "half-adder" (quello sulla cifra meno
significativa
somma 1 ad a0, quelli sulle cifre successive
sommano ai+ri).
In questo caso anche la funzione "carry
lookahead" può
essere estremamente semplificata:
ri = ai-1 · ai-2 · ... · a0
Scopo di un circuito comparatore é il confronto tra due codifiche binarie. Il confronto può essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo "maggiore", "minore", ecc. Il caso di confronto per stabilire l'uguaglianza può essere risolto in maniera molto semplice ed indipendente dal codice usato, con l'unica ipotesi di avere una rappresentazione unica per ogni valore. I confronti per stabilire relazioni d'ordine invece devono necessariamente tener conto del codice utilizzato.
Questi possono essere realizzati a partire dalla funzione elementare XNOR a due ingressi. Dalla tavola di verità di questa funzione vediamo che, interpretando l'uscita 0 come "falso" e l'uscita 1 come "vero", possiamo ottenere immediatamente in uscita il risultato del confronto per rilevare l'uguaglianza tra le due variabili di ingresso.
Possiamo estendere il circuito in modo da operare il confronto tra due insiemi di variabili booleane, utilizzando una funzione del tipo XNOR per ogni coppia di variabili da confrontare, calcolando poi l'AND tra i confronti di ogni cifra. Per esempio, in figura é illustrata la realizzazione di un circuito comparatore per rilevare l'uguaglianza tra due ingressi codificati ciascuno su 3 bit (usando ovviamente lo stesso codice per i due ingressi).
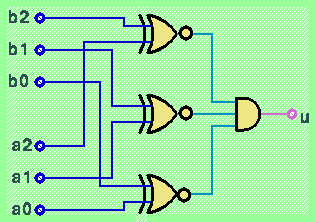
Cominciamo a considerare il caso di rappresentazioni di numeri senza segno su 2 bit. La seguente Mappa di Karnaugh descrive il funzionamento del circuito che vogliamo realizzare:
\ b1 | 0 : 0 : 1 : 1 |Un esempio di realizzazione di questa mappa é dato dalla funzione:
\ b0 | 0 : 1 : 1 : 0 |
a1 a0 \ | : : : |
--------\--+-----:-----:-----:-----+
0 0 | 0 : 0 : 0 : 0 |
..........|.....:.....:.....:.....|
0 1 | 1 : 0 : 0 : 0 |
..........|.....:.....:.....:.....|
1 1 | 1 : 1 : 0 : 1 |
..........|.....:.....:.....:.....|
1 0 | 1 : 1 : 0 : 0 |
-----------+-----:-----:-----:-----+
u = a1 · ¬b1 + a0 · ¬b0 · ¬b1 + a0 · a1 · ¬b0
La complessità della realizzazione tuttavia cresce molto in funzione del numero di bit delle codifiche da confrontare. Nel caso di confronto tra numeri codificati su 3 bit otteniamo la mappa:
\ b2 | 0 : 0 : 0 : 0 : 1 : 1 : 1 : 1 |Un esempio di realizzazione di questa mappa é dato dalla funzione:
\ b1 | 0 : 0 : 1 : 1 : 0 : 0 : 1 : 1 |
\ b0 | 0 : 1 : 0 : 1 : 0 : 1 : 0 : 1 |
a2 a1 a0 \ | : : : : : : : |
-----------\--+-----:-----:-----:-----:-----:-----:-----:-----+
0 0 0 | 0 : 0 : 0 : 0 : 0 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
0 0 1 | 1 : 0 : 0 : 0 : 0 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
0 1 0 | 1 : 1 : 0 : 0 : 0 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
0 1 1 | 1 : 1 : 1 : 0 : 0 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
1 0 0 | 1 : 1 : 1 : 1 : 0 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
1 0 1 | 1 : 1 : 1 : 1 : 1 : 0 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
1 1 0 | 1 : 1 : 1 : 1 : 1 : 1 : 0 : 0 |
.............|.....:.....:.....:.....:.....:.....:.....:.....|
1 1 1 | 1 : 1 : 1 : 1 : 1 : 1 : 1 : 0 |
--------------+-----:-----:-----:-----:-----:-----:-----:-----+
u = a2·(¬b2) + a1·(¬b1)·(a2+(¬b2)) +a0·(¬b0)·(a2·(a1+(¬b1))+(¬b2)·(a1+(¬b1)))
Si vede bene come l'estensione di questo circuito al caso di più di 3 bit di rappresentazione per i numeri da confrontare diventa improponibile (almeno dal punto di vista della derivazione manuale delle mappe e della funzione che realizza il circuito).
L'alternativa consiste quindi nell'individuare un modulo base di confronto tra una coppia di cifre, e nel replicare tale modulo tante volte quante sono le cifre delle rappresentazioni binarie da confrontare.
L'approccio modulare può basarsi su due algoritmi diversi per il confronto.
Il primo corrisponde al procedimento standard che abbiamo imparato fin dalle elementari per ordinare le parole del vocabolario italiano (ordinamento lessicografico) che possiamo specificare in forma di pseudo-codice:
for i=N-1..0
if ai≠bi
return ai > bi
return false
Nota bene Questo è l'algoritmo sensato per un'implementazione software
Il confronto parte dalla cifra più significativa: se le due rappresentazioni differiscono nella cifra più significativa, allora possiamo subito concludere se la relazione a>b é vera o falsa, senza bisogno di considerare le cifre successive. Solo se le cifre più significative delle due rappresentazioni a confronto sono uguali, allora dobbiamo passare all'esame delle cifre successive per arrivare a concludere il valore di verità della relazione di confronto.
Tale algoritmo iterativo può essere tradotto nella definizione di un schema logico circuitale composto da N moduli, ognuno dei quali confronta i bit di a e b in una determinata posizione i e collegati in cascata in modo che l'informazione fluisca dal modulo corrispondente alla posizione più significativa (i=N-1) fino a quello della posizione meno significativa (i=0). Visto che l'uscita anticipata dal ciclo for non può essere tradotta a livello di circuito combinatorio, l'algoritmo implementato diventerebbe:
res=false
done=false
for i=N-1..0
if not done and ai≠bi
done=true
res=ai > bi
return res
Quindi, un generico modulo alla posizione i dovrebbe avere 4 ingressi per i valori di ai, bi e di res e done (per il ciclo i-mo), e 2 uscite per i valori di res e done per il ciclo i+1-mo.
Vediamo ora cosa succederebbe se partissimo a confrontare prima i bit meno significativi, ossia se le informazioni fluissero a partire dal modulo di posizione 0 fino a quello di posizione N-1:
res=false
for i=0..N-1
if ai≠bi
res=ai > bi
return res
Quest'ultima soluzione è più semplice poiché non abbiamo bisogno di usare la variabile done. Tale semplicità si riflette sulla progettazione dei moduli che avranno solo 3 ingressi a, b e res e 1 uscita res', il cui comportamento è specificato dalla seguente mappa, da cui si ricava la formula minimale res' = a · res + a · ¬ b + res · ¬ b.
| a b / res | 0 | 1 |
|---|---|---|
| 00 | 0 | 1 |
| 01 | 0 | 0 |
| 11 | 0 | 1 |
| 10 | 1 | 1 |
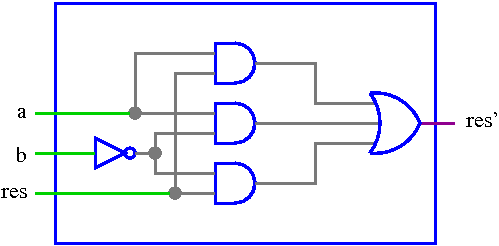
Un comparatore che calcola a3a2a1a0 > b3b2b1b0 può
essere facilmente assemblato connettendo 4 moduli nel seguente modo:
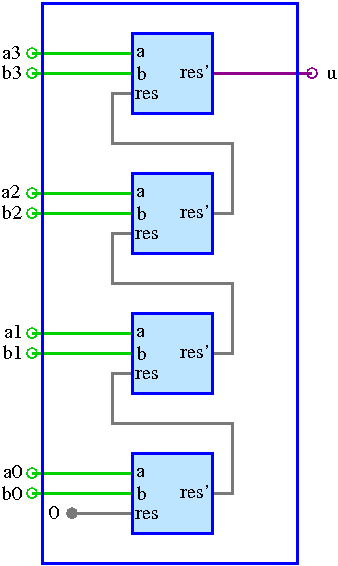
Vediamo invece come la soluzione che parte dai bit più significativi sia più complessa. Ogni modulo ha 4 ingressi a, b, d (=done), r (=res) e 2 uscite d' (=done') ed r' (=res') e un comportamento specificato dalla seguente mappa:
| a b / d r | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 00 | 01 | 11 | 10 |
| 01 | 10 | 10 | 11 | 10 |
| 11 | 00 | 01 | 11 | 10 |
| 10 | 11 | 11 | 11 | 10 |
d'=d+(a xor b)
r'= d·r + a·r + a·¬b·¬d + ¬a·¬b·r
Infine qualche considerazione su confronto tra numeri interi; i comparatori per numeri naturali possono essere utilizzati anche per il confronto tra numeri con segno in codice eccesso 2**(N-1). Nel caso di numeri con segno in codice complemento a 2 occorre invece invertire la cifra più significativa delle due rappresentazioni (il bit di segno).
La funzione di cambiamento di segno per un numero rappresentato in codice complemento a 2 su N bit può essere realizzata, oltre che (partendo dalla definizione) complementando a 1 e poi sommando la costante 1, anche mediante un algoritmo iterativo che esamina tutte le cifre della rappresentazione partendo da quella meno significativa. L'algoritmo prevede due comportamenti diversi in funzione di una variabile di stato. Nello stato iniziale, si esamina la cifra corrente (partendo dalla meno significativa) e la si lascia invariata; se la cifra corrente é 1 allora si passa al secondo stato, altrimenti si rimane nello stato iniziale. Nel secondo stato si complementa la cifra corrente e si permane nel secondo stato.
Tale algoritmo può essere realizzato mediante l'adozione di un modulo circuitale combinatorio a 2 ingressi (denominati I e C) e due uscite (denominate U e S), in grado di calcolare una cifra della rappresentazione del risultato. Il modulo "complementatore a 2" viene specificato mediante la seguente tavola di verità:
c2 : S C | U S'
-------+------
0 0 | 0 0
0 1 | 1 1
1 0 | 1 1
1 1 | 0 1
Ovviamente la realizzazione del dispositivo può essere ottenuta mediante una funzione XOR per l'uscita U ed una funzione OR per l'uscita S'.
Un circuito complementatore a 2 per rappresentazioni su N bit viene quindi ottenuto usando N copie del modulo realizzato come sopra specificato. L'ingresso C di ciascun modulo viene connesso a una cifra della rappresentazione del numero da cambiare di segno. L'uscita U del modulo rappresenta la corrispondente cifra della rappresentazione del risultato. L'ingresso S del modulo corrispondente alla cifra meno significativa viene connesso al valore costante 0. L'ingresso S di tutti gli altri moduli viene connesso all'uscita S' del modulo che calcola la cifra immediatamente precedente.
Come nel caso del sommatore con ripple carry, questo circuito ha una complessità di realizzazione che cresce linearmente col numero di bit della rappresentazione del numero, ed un tempo di assestamento dei risultati in uscita a seguito di variazioni dei valori in ingresso che cresce anch'esso linearmente col numero di bit della rappresentazione.
Anche nel caso di circuiti per la moltiplicazione tra numeri espressi in codice binario senza segno su N bit, una realizzazione in logica a tre livelli risulterebbe eccessivamente complessa per grandi valori di N. Vediamo quindi subito una realizzazione modulare. Il punto di partenza per una realizzazione modulare é il cosiddetto algoritmo di moltiplicazione per "somme e scorrimenti", versione binaria del normale algoritmo di moltiplicazione cifra per cifra a cui siamo abituati nel sistema decimale.
Cominciamo a considerare il caso semplificato di moltiplicazione di un operando A rappresentato su N cifre per un operando b rappresentato su una sola cifra binaria. L'operando b potrà assumere ovviamente solo i valori 0 e 1. Nel primo caso il risultato del prodotto sarà 0, mentre nel secondo caso il risultato sarà A. Tale risultato può essere ottenuto mediante un circuito combinatorio composto da N funzioni AND a 2 ingressi, ciascuna connessa ad una cifra diversa dell'operando A ed all'unica cifra dell'operando b. Ogni funzione AND produrrà in uscita una cifra del risultato del prodotto.
Consideriamo ora il caso di un operando A espresso su N bit, ed un operando B espresso su due bit (ovvero B=b0+2·b1). Il prodotto A·B può quindi essere decomposto in A·b0 + A·b1·2, dove l'operazione di moltiplicazione per 2 viene realizzata mediante lo "scorrimento" della rappresentazione del numero di una cifra verso sinistra, aggiungendo 0 come cifra meno significativa.
Da questo possiamo arrivare a produrre uno schema di realizzazione di un circuito moltiplicatore tra due numeri rappresentati su N bit che fa uso solo di circuiti sommatori e di funzioni AND. Un tale moltiplicatore può essere istanziato al caso di N=3 come illustrato in figura a titolo di esempio:
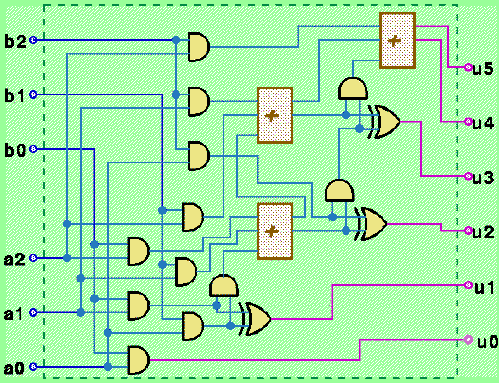
La complessità circuitale di un dispositivo di questo tipo cresce col quadrato del numero di bit delle rappresentazioni degli operandi (il numero di somme e di moltiplicazioni per un bit cresce linearmente col numero di bit, e la realizzazione di ciascuno cresce linearmente col numero di bit). Dal punto di vista del tempo di assestamento, questo può crescere secondo N·log(N), utilizzando uno schema di somma ad albero binario (si possono costruire degli alberi binari di sommatori di profondità logaritmica rispetto al numero di termini da sommare, ed ogni sommatore di tipo ripple carry richiede un tempo di assestamento che cresce linearmente col numero di bit).
L'unità aritmetico-logica é uno dei componenti fondamentali di un sistema di calcolo. Viene solitamente realizzata come circuito combinatorio con due insiemi di variabili di ingresso (contenenti la codifica binaria di due operandi), un insieme di variabili di controllo, un insieme di variabili di uscita (contenente la codifica di un risultato), ed eventualmente altre variabili di uscita contenenti la codifica di condizioni particolari verificatesi durante il funzionamento del circuito.
Un'ALU é in grado di produrre un risultato in uscita corrispondente all'applicazione di diversi operatori aritmetici (somma, moltiplicazione, ecc.) o logici (AND, NOT, ecc.) agli operandi codificati sulle variabili di ingresso. La scelta del tipo di operazione da effettuare avviene attraverso una codifica binaria fornita all'ALU mediante gli ingressi di controllo. Le condizioni segnalate sono solitamente overflow per operazioni aritmetiche, risultato uguale a zero, risultato negativo, ecc.
La realizzazione di un'ALU operante su rappresentazioni ad N bit
può essere ottenuta mediante l'unione di tanti circuiti
combinatori, ciascuno specializzato nel calcolo di una funzione unaria
(complementatore a 2,
NOT, moltiplicatore per 2, ecc.) o binaria (sommatore, AND, OR, ecc.)
su N bit,
tutti connessi alle stesse rappresentazioni di operandi in ingresso,
connessi alternativamente in uscita mediante un multiplexer comandato
dai
segnali di controllo dell'ALU.
La complessità della realizzazione cresce sia al crescere del numero N
di
bit di rappresentazione degli operandi, sia al crescere del numero di
operatori
aritmetici e logici inclusi.