Copyright © 1996-2003.
Questo documento é protetto dalla legge sul diritto di autore, e di proprietà esclusiva dell'autore che se ne riserva tutti i diritti.
L'autore concede a chiunque il permesso di copiare gratuitamente qualunque sottoinsieme dei files che compongono questi appunti per qualsiasi uso e su qualsiasi supporto, purchè la copia di ciascun file sia integrale, senza alcuna modifica ad eccezione di un eventuale cambiamento di formato di rappresentazione per necessità di stampa o memorizzazione su sistemi diversi, e purchè ogni copia sia sempre accompagnata dalla presente clausola completa di Copyright.
Le informazioni presenti in questo documento distribuito dall'autore in forma gratuita vengono fornite in quanto tali, senza nessuna garanzia di correttezza, consistenza o assenza di errori da parte dell'autore stesso, il quale per altro declina ogni responsabilità per qualsiasi danno o inconveniente che potesse derivare dall'uso del documento stesso, anche se si dovesse verificare il caso che talune informazioni qui contenute non fossero corrette.
É permessa anche la riutilizzazione parziale o totale del testo e delle figure per la produzione di lavori derivati, purchè i lavori derivati siano soggetti alle condizioni di diffusione ed uso di questo documento originale, con particolare riferimento alla possibilità per chiunque di copiare liberamente e senza restrizione alcuna il documento in forma integrale e di usarne parti per la creazione di lavori derivati soggetti alle medesime condizioni di diffusione ed uso. Nel caso di creazione di lavori derivati mediante inclusione e/o modifica sostanziale del testo originale, l'autore delle modifiche si assumerà la paternità delle aggiunte e delle modifiche, ed il nome dell'autore del testo originale non potrà essere utilizzato senza il suo preventivo ed esplicito consenso per patrocinare l'opera derivata.
Le condizioni di questo Copyright sono liberamente ispirate al
"copyleft"
originariamente introdotto da Richard Stallman, e dovrebbero essere
una versione semplificata ma sostanzialmente equivalente alla
"Free Documentation
License" raccomandata dalla
"Free Software Foundation".
NOTA PRELIMINARE: questa prima parte introduttiva agli argomenti del corso, insieme con una parte del materiale sui codici viene ora svolta nell'ambito del corso di Informatica Generale. Viene mantenuta in questi appunti per completezza di trattazione, e costituisce un prerequisito per la comprensione del resto del programma effettivamente svolto nel corso di Architettura dei Calcolatori.
Una delle caratteristiche peculiari dei Sistemi di Calcolo, che ne ha accompagnato l'evoluzione sin dalle origini negli anni '40, é la complessità. Tale caratteristica si riperquote in diverse attività di un "informatico" quali la progettazione, realizzazione, uso, comprensione di un sistema di calcolo.
Al fine di poter trattare sistemi molto complessi, gli informatici hanno sviluppato una serie di "contromisure", tra le quali la più efficace é la decomposizione in livelli di astrazione diversi. Tale decomposizione viene ottenuta normalmente attraverso l'introduzione dei concetti di Macchina Virtuale, Linguaggio e di Codifica delle informazioni.
Si possono dare delle definizioni matematiche rigorose di tali concetti. Definiamo l'alfabeto di una macchina virtuale come un insieme finito di simboli diversi tra loro riconoscibili ed utilizzabili dalla macchina virtuale. Il linguaggio della macchina virtuale é definito come la descrizione di tutte le sequenze di simboli dell'alfabeto che identificano dei comandi eseguibili dalla macchina virtuale o dei dati usati o prodotti dalla macchina virtuale durante l'esecuzione dei comandi.
Prima di addentrarci nello studio dei sistemi di calcolo con l'ausilio del concetto di macchina virtuale é utile fare qualche considerazione "di buon senso" basata sulla esperienza quotidiana di ciascuno di noi. É infatti importante comprendere che l'informatica ed i sistemi di calcolo non sono estranei alla vita quotidiana, e questo non soltanto perché una quota sempre maggiore di elettrodomestici e strumenti di uso comune fanno uso di tecnologie informatiche, ma anche perché molto spesso noi stessi ragioniamo in termini informatici (probabilmente senza neanche rendercene conto).
Cominciamo quindi a considerare un esempio dalla vita domestica: l'uso di una lavabiancheria per il bucato. Indipendentemente dalla presenza di un "microprocessore" all'interno della macchina (molto probabile in un modello recente), possiamo subito individuare una peculiarità di questo elettrodomestico di potersi adattare a diversi tipi di tessuti da lavare ed a diversi livelli di risultati in termini di bucato prodotto.
Tipicamente, dopo aver inserito il bucato ed il detersivo, dobbiamo girare una o più manopole (oppure premere pulsanti) per la scelta del tipo di lavaggio desiderato. Alternative tipiche possone essere: "Cotone", "Colorati", "Sintetici", "Lana", ecc. Tali nomi formano ciò che in termini informatici viene detto un "linguaggio" (nel nostro caso particolare si tratta di un linguaggio degenere che si riduce ad un semplice vocabolario) mediante il quale noi possiamo impartire ordini che verranno eseguiti alla lettera dalla macchina, senza alcun controllo "intelligente". Per esempio, se inseriamo nella macchina dei tessuti con colori delicati, e la programmiamo per l'attivazione di un ciclo di lavaggio adatto per lenzuola bianche, la lavabiancheria eseguirà l'ordine ricevuto riscaldando l'acqua alla temperatura di 90 gradi, con risultati disastrosi per il bucato. É compito dell'utilizzatore di impartire alla macchina ordini coerenti utilizzando il linguaggio di programmazione descritto sul manuale d'uso.
La comprensione del manuale d'uso e l'uso della lavabiancheria prescindono da come la macchina realizza effettivamente il lavaggio. Quando la nostra macchina si guasta, il tecnico della manutenzione che viene ad effettuare la riparazione userà delle descrizioni dello stesso elettrodomestico diverse dal manuale d'uso (schemi elettrici, catalogo delle parti, ecc.) per portare a termine la riparazione, evidenziando quindi un modo totalmente diverso di osservare e manipolare la stessa macchina (un diverso livello di astrazione).
Passiamo ad un esempio più complesso: il problema di procurarsi una pizza per mangiare. Possiamo anzitutto scegliere tra due alternative: cucinare la pizza in proprio, oppure recarsi in una pizzeria. Cominciamo ad esaminare la prima alternativa.
Per cucinare la pizza in casa occorre procurarsi gli ingredienti (acqua, farina, lievito, ecc.), la ricetta (per esempio da un libro di cucina), ed una serie di attrezzi per la realizzazione della ricetta (mattarello, tavolo, forno, ecc.). Una volta procurate tutte queste cose possiamo passare alla fase di preparazione, seguendo i passi descritti nella ricetta.
La ricetta farà uso di un linguaggio che noi dobbiamo essere in grado di comprendere correttamente e dovrà descrivere il procedimento di preparazione in termini di passi elementari che noi dobbiamo essere in grado di realizzare. Se per esempio la ricetta fosse scritta in dialetto napoletano noi dovremmo sapere che il termine "pummarola" indica la passata di pomodoro. D'altra parte, se leggendo la ricetta incontriamo l'istruzione "scaldare il forno", dobbiamo essere in grado di accendere il forno e portarlo alla temperatura corretta; le procedure possono essere diverse per un forno a legna, a gas o elettrico, e non é detto che una persona in grado di scaldare un forno elettrico sia capace di scaldare correttamente anche un forno a legna, nel qual caso avrebbe bisogno di istruzioni più dettagliate per poter portare a termine correttamente l'operazione.
In termini informatici, la realizzazione di una pizza seguendo passo passo le indicazioni di una ricetta costituisce una attività detta interpretazione da parte di una macchina virtuale (noi stessi nella fattispecie).
L'eventuale interruzione della interpretazione della ricetta al momento del riscaldamento del forno per andare a leggere su un altro manuale le istruzioni dettagliate di accensione e regolazione della temperatura, in termini informatici costituisce una estensione procedurale per sopperire ad una mancanza di corrispondenza precisa tra le istruzioni contenute nella ricetta (programma da eseguire) e l'insieme delle istruzioni che la macchina virtuale (noi stessi) conosce ed é in grado di eseguire direttamente. Al termine dell'interpretazione della procedura "scaldare il forno" la macchina virtuale può tornare all'interpretazione del programma principale, dal punto in cui l'aveva interrotto.
La seconda alternativa può risultare più dispendiosa ma anche più comoda, in quanto qualcun altro svolgerà il ruolo di macchina virtuale al posto nostro. Normalmente, in pizzeria l'interazione avviene con un cameriere, il quale assume agli occhi del cliente il ruolo di macchina virtuale.
Inizialmente, il linguaggio usato per la comunicazione tra cliente e cameriere sarà quello dei nomi delle pizze scritte sul menù ("margherita", "quattro stagioni", "napoletana", ecc.). Tale linguaggio può essere considerato ad alto livello, in quanto ogni parola corrisponde direttamente con una particolare esigenza dell'utilizzatore della macchina. Ordinando al cameriere "una quattro stagioni" noi comandiamo alla macchina virtuale pizzeria l'esecuzione di una attività complessa, il cui risultato é quello di far arrivare al nostro tavolo la pizza desiderata. L'utente tuttavia non é normalmente interessato ai dettagli di realizzazione della pizza, per cui si pone ad un livello di astrazione superiore e percepisce l'attività della macchina virtuale pizzeria come un tutt'uno che termina con il recapito della pizza desiderata al proprio tavolo dopo una certa quantità di tempo.
Il cameriere si pone invece ad un livello di astrazione inferiore per poter realizzare la macchina virtuale con le funzionalità richieste dal cliente sulla base delle macchine virtuali di cui lui stesso può disporre. Tipicamente il cameriere scriverà l'ordine su un pezzo di carta col duplice scopo di passare l'ordine al pizzaiolo e di tener traccia della consumazione per poter poi presentare il conto. Normalmente, per risparmiare tempo, userà delle convenzioni per codificare in forma abbreviata l'ordine ricevuto dal cliente; per esempio qualcuno potrebbe scrivere "4S" (al posto di "quattro stagioni"), qualcun altro potrebbe scrivere "X4", qualcun altro ancora potrebbe scrivere "2" (se il nome "quattro stagioni" compare al secondo posto nella lista dei nomi del menù, come nel nostro esempio).
Una volta trascritto l'ordine, il cameriere passa l'ordine al pizzaiolo e può dedicarsi al servizio di un altro tavolo, demandando quindi il completamento dell'esecuzione dell'istruzione ad un'altra macchina virtuale (per un produttore di automobili questa tecnica verrebbe chiamata "catena di montaggio", mentre gli informatici preferiscono usare il termine pipeline).
La macchina virtuale pizzaiolo interpreta gli ordini ricevuti dal cameriere mediante applicazione di una serie di passi elementari che ha imparato ad eseguire una volta per tutte e che ricorda in permanenza (stendere la pasta, aggiungere la passata di pomodoro, aggiungere la mozzarella, ecc.). In termini informatici, il pizzaiolo esegue una istruzione della sua macchina virtuale interpretando una sequenza di micro istruzioni presenti in una sua memoria permanente (firmware) ed univocamente associate a ciascun codice che il cameriere scrive sull'ordine.
L'esecuzione delle micro istruzioni può essere interrotta solo
nel caso si manifestino delle eccezioni (o trap),
ad esempio per esaurimento degli ingredienti o per mancato riconoscimento
del codice di un comando.
Il trattamento di una eccezione può comportare un ritardo nel completamento
dell'esecuzione del comando (per esempio chiedendo a voce al cameriere di
chiarire che tipo di pizza era stato richiesto, a causa della sua brutta
calligrafia) o l'aborto (col cameriere che torna dal cliente e si
scusa di non poter soddisfare l'ordine a causa dell'esaurimento dei carciofini).
Ragionando in termini puramente astratti possiamo quindi concludere che ogni istruzione del livello L5 (per esempio ogni istruzione del linguaggio Pascal) può essere descritta in termini di sequenze di istruzioni del livello L1. Questo é vero anche in termini pratici: potremmo pensare di monitorare e registrare il comportamento dei dispositivi fisici che compongono il sistema di calcolo al livello L1, ed associare una serie complessa di attività all'esecuzione di una singola istruzione di livello L5. Concettualmente potremmo quindi arrivare a concludere che la stratificazione proposta nella tabella non ha motivazioni teoriche per esistere, in quanto i programmi potrebbero essere scritti dal programmatore direttamente usando il linguaggio della macchina virtuale L1, invece del Pascal. Questo tentativo di "semplificazione" del problema é destinato a fallire miseramente in quanto non tiene conto di un vincolo fondamentale: il limite intrinseco alle capacità cognitive del programmatore destinato ad usare la macchina virtuale sistema di calcolo. Nessuno di noi riuscirebbe a raccapezzarsi nella descrizione di alcune decine o centinaia di migliaia di istruzioni elementari del livello di astrazione L1 corrispondenti a poche istruzioni di un programma Pascal per la somma di due numeri interi e la stampa del risultato.
Scopo della stratificazione in livelli di astrazione é dunque quello di colmare il divario (semantic gap) tra il modo di pensare alla soluzione dei problemi da parte del programmatore ed il modo di realizzare delle macchine che sfruttando fenomeni fisici conosciuti siano in grado di eseguire il programma che porta alla soluzione del problema. Tale tecnica viene applicata più volte nel caso di soluzione di problemi complessi: anche lavorando con una macchina virtuale di livello L5 il programmatore può sentire la necessità (o sfruttare l'opportunità) di definire una ulteriore stratificazione in livelli di astrazione diversi, a cui corrisponde una pila di macchine virtuali destinate a colmare il divario tra le istruzioni fornite dal linguaggio di programmazione e il suo modo di risolvere concettualmente un problema complesso.
In questo corso introduttivo non verranno trattati i livelli di indice inferiore a zero per diversi motivi, tra i quali la mancanza delle basi matematiche per la comprensione delle equazioni che descrivono il comportamento dei semiconduttori e la limitata offerta di lavoro (anche a livello internazionale) per persone specializzate in questi aspetti. I livelli da L0, L1 e L2 costituiscono il punto di vista hardware di un sistema di calcolo, mentre dal livello L3 in su si passa al punto di vista del software (di base, o di sistema). Del livello software L3 verrano trattati solo alcuni aspetti strettamente legati all'interazione con l'hardware demandando al corso di Sistemi Operativi tutti gli aspetti di gestione delle risorse. Gli argomenti del corso di Architettura vertono essenzialmente sui livelli L1 e L2, dopo una breve introduzione sul livello L0.
Prima di passare ad una analisi dal basso verso l'alto (bottom-up)
della pila dei livelli di astrazione da L0 ad L2 durante la quale definiremo
delle macchine virtuali via via più complesse a partire da funzioni Booleane
elementari, apriremo tuttavia una parentesi introduttiva sulla realizzazione di
macchine a livello L2, prendendo spunto dalla effettiva evoluzione storica
dei primi sistemi di calcolo negli anni '40 e '50.
Useremo una versione "astratta" riveduta e semplificata della
Macchina di Von Neumann per cominciare ad avere un esempio dei livelli
L1 ed L2 su cui verificare la comprensione dei concetti fondamentali,
e da intendere anche come motivazione per lo studio del livello L0.
Nella seconda parte del corso verranno poi introdotte man mano le caratteristiche
delle odierne architetture RISC e CISC, in modo da comprendere quanto meno su
quali principi si basano i sistemi odierni in grado di fornire prestazioni
superiori di parecchi ordini di grandezza rispetto ai sistemi tradizionali.
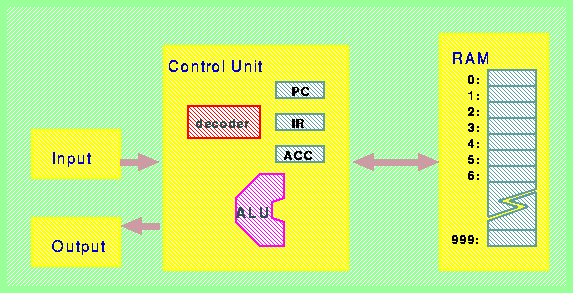
La macchina é realizzata mediante l'interconnessione di quattro dispositivi complessi: memoria, unità operativa, ingresso e uscita, come illustrato in figura:

L'unità di controllo é realizzata in modo da poter eseguire (direttamente oppure comandando parte dell'esecuzione alle altre unità della macchina) un insieme finito di istruzioni. Sempre a titolo esemplificativo potremmo individuare un insieme di nove istruzioni base.
L'idea fondamentale di Von Neumann, che viene ancora oggi seguita nella realizzazione dei sistemi di calcolo fu quella di codificare le istruzioni in forma numerica, e di inserirle, insieme agli eventuali dati, nella unità RAM della macchina. Un modo molto semplice per ottenere una codifica numerica per l'identificazione delle istruzioni é quella di elencarle in una lista ordinata, e di usare il numero d'ordine all'interno della lista per individuare l'istruzione. Proviamo a considerare il seguente esempio:
Supponendo di saper codificare qualsiaso istruzione (compresi i suoi eventuali operandi) sotto forma numerica in una singola cella di RAM, allora possiamo individuare una modalità di funzionamento sequenziale per la nostra macchina facendo uso del registro PC, esprimibile con il seguente algoritmo:
Il caricamento di programmi sequenziali nella RAM (codificati in forma numerica) costituisce quindi un mezzo semplice ma molto efficace per definire sequenze di istruzioni (anche molto lunghe) che la macchina dovrà eseguire una volta attivata (per esempio attraverso la pressione di un apposito pulsante).
Le istruzioni 6, 7 e 8 servono per alterare l'esecuzione sequenziale di programmi codificati in memoria. L'istruzione 6 viene chiamata normalmente salto di programma, in quanto determina una interruzione nella continuità della scansione della RAM in forma sequenziale: fa si che la prossima istruzione da eseguire venga decodificata a partire dal contenuto della cella RAM[N] anziché dal contenuto della cella di indirizzo successivo rispetto a quella che contiene la codifica dell'istruzione di salto. L'istruzione 7 viene chiamata (per ovvie ragioni) salto condizionale. Notare che anche le istruzioni 6 e 7 richiedono la codifica di un parametro numerico oltre all'individuazione della istruzione, mentre l'istruzione 8 é priva di parametri.
Un algoritmo semplice per ottenere la codifica numerica di tutte le istruzioni, comprese quelle con un operando, consiste nel moltiplicare per 1000 il numero d'ordine dell'istruzione e sommare il valore dell'eventuale operando (sempre compreso tra 0 e 999 a causa della limitazione sulla dimensione della RAM). La decodifica verra' effettuata prendendo la parte intera della divisione del valore numerico diviso 1000 per ottenere il numero d'ordine dell'istruzione, ed il resto di questa stessa divisione come valore dell'indirizzo della cella di memoria da usare come operando.
Il nostro programma per la stampa della somma di due numeri corrisponderà quindi a caricare in memoria i seguenti valori prima di attivare l'esecuzione della macchina:
Notare che il programma potrebbe funzionare altrettanto bene se sostituissimo i valori contenuti nelle celle RAM[1] con 4000 e RAM[3] con 0. Notare anche che con tale sostituzione la stessa cella RAM[0] verrebbe utilizzata (in tempi diversi) per contenere prima la codifica della prima istruzione del programma e poi (dopo che tale istruzione é stata eseguita) il valore del primo addendo letto dal dispositivo di ingresso. Una tale variazione potrebbe aver senso in questo caso per "risparmiare" l'uso di una cella di memoria, tuttavia riduce la capacità del programmatore di comprendere il funzionamento del programma e garantirne la correttezza. In effetti, per garantire la correttezza di una tale utilizzazione ottimizzata della memoria bisogna essere certi che l'istruzione di cui si perde memoria non dovrà mai più essere eseguita nel prosieguo dell'interpretazione del programma. Per esempio l'utilizzazione della cella RAM[2] (ottenuta sostituendo i valori 4002 nella cella RAM[1] e 2 nella cella RAM[3]) porterebbe ad un programma errato (a meno che, per pura coincidenza, l'utente non decida di specificare il valore 2000 come primo addendo).
Per verificare il livello di comprensione circa la possibilità di programmare una macchina di questo genere proviamo ad organizzare una modifica dell'esempio proposto in modo da poter ripetere indefinitamente l'operazione di somma tra due numeri e stampa del risultato, fin quando non si incontra un addendo uguale a zero (nel qual caso il programma deve terminare). Per realizzare questa modifica occorre prevedere l'aggiunta di istruzioni di tipo 6 (per ripetere indefinitamente la sequenza delle istruzioni dall'inizio) e di tipo 7 (per distinguere il caso di addendo uguale a zero da quello di addendo diverso da zero). Una possibile realizzazione sotto forma di programma é la seguente:
In effetti, l'unità di controllo applica l'algoritmo di fetch e decodifica delle istruzioni in modo indiscriminato, sulla base del valore assunto dal registro PC, senza aver alcun modo per sapere se il valore inserito nel registro IR fosse stato effettivamente memorizzato nella cella RAM[PC] con lo scopo di codificare una istruzione oppure di mantenere un valore numerico. É responsabilità del programmatore far si che la cella da cui viene fatto il fetch contenga effettivamente un numero che rappresenta l'istruzione che si vuol eseguire in quel momento e non un qualsiasi altro numero.
Un programma che prima inserisce un dato in una cella di memoria e poi successivamente passa ad interpretare il contenuto di quella stessa cella di memoria come la codifica di una istruzione (accedendovi in fase di fetch) viene detto automodificante. Un programma automodificante non é necessariamente errato, anzi nella macchina di von Neumann alcuni problemi possono essere risolti solo mediante l'uso di programmi automodificanti. Oggi nessun programmatore concepisce programmi automodificanti, anche grazie ai progressi fatti nella organizzazione delle macchine convenzionali: al contrario, nei moderni sistemi di calcolo la memoria viene partizionata in aree specializzato per contenere i dati distinte da quelle destinate a contenere il codice del programma da eseguire, ed il tentativo di cambiare il contenuto delle celle contenenti il programma provoca normalmente la terminazione del programma stesso con un messaggio di errore.
Fin'ora abbiamo considerato il caso in cui il programma desiderato dall'utente sia stato in qualche modo (magicamente?) inserito nella RAM sotto forma di codifica numerica delle istruzioni. Da un punto di vista pratico si pone però il problema di inserire questi numeri all'interno della RAM prima di far partire l'unità di controllo col fetch della prima istruzione. Per risolvere questo problema la macchina viene normalmente fornita dal costruttore provvista di un insieme di programmi predefiniti, comunemente indicati col termine Sistema Operativo, che hanno lo scopo di facilitare l'uso della macchina stessa fornendo all'utente delle modalità semplici di caricamento dei programmi in memoria e lancio della loro esecuzione.
In particolare nel nostro caso possiamo pensare di risolvere il problema con un semplice programma di Bootstrap che legga dal dispositivo di ingresso prima l'indirizzo della prima cella del programma, poi la sequenza dei codici operativi delle istruzioni del programma, li inserisca in celle di memoria consecutive, ed alla fine passi (mediante l'esecuzione di una istruzione di salto condizionale) al fetch della cella di memoria nella quale é stata caricata la codifica numerica della prima istruzione.
La nostra variante di macchina di Von Neumann é stata introdotta come un esempio di macchina convenzionale. La descrizione che ne abbiamo dato per descriverne il funzionamento usa i concetti, la terminologia e la notazione del livello di microarchitettura.
In realtà la nostra stratificazione ha senso solo quando consideriamo due o più livelli diversi contemporaneamente. In particolare, l'uso che facciamo della stratificazione é quello di descrivere (o progettare, o realizzare) un livello di astrazione più alto utilizzando uno (o più) livelli di astrazione noti (o disponibili). Ciò vale per qualsiasi livello di macchina virtuale. É naturale quindi aspettarsi che per la descrizione di una macchina virtuale di livello Li si faccia uso di descrizioni appartenenti a livelli Lj, con j minore o uguale ad i.
La macchina convenzionale propriamente detta (ossia il livello di astrazione L2 della nostra macchina) comprende la definizione dei registri accumulatore e PC, la dimensione della memoria, e l'insieme delle istruzioni (ossia la specifica di come manipolano il contenuto delle celle di memoria e dei registri) della macchina. Il resto della descrizione (registro IR, algoritmo di fetch, ecc.) appartengono al livello di astrazione L1.
In questo caso il livello 3 della macchina potrebbe essere costituito semplicemente dall'esempio di programma di bootstrap. Il livello 4 potrebbe prevedere la definizione una volta per tutte di alcuni "pezzi di programma" per risolvere semplici problemi, da poter riutilizzare in diverse circostanze. Tuttavia la preparazione di vere e proprie librerie di funzioni predefinite si scontra con la rigidità del meccanismo di indirizzamento (solo diretto) e con l'assenza di istruzioni di chiamata e ritorno da sottoprogramma. Per risolvere entrambi i problemi occorre in questo caso sfruttare appropriatamente la possibilità di definire programmi automodificanti.
Una delle tecniche classiche di programmazione é l'estensione procedurale. L'idea consiste nel definire una volta per tutte dei "sottoprogrammi" di utilità generale, che possano essere richiamati da altri programmi per portare a termine parte del compito prefisso. L'esigenza di questi sottoprogrammi nasce dalla limitatezza dell'insieme delle istruzioni base della macchina: la mancanza di una istruzione macchina capace di risolvere immediatamente un sottoproblema stimola l'introduzione di una estensione procedurale che permetta la soluzione di tale sottoproblema una volta per tutte.
Consideriamo il caso di una istruzione di moltiplicazione tra due numeri. Tale istruzione non é presente nel repertorio della nostra macchina di Von Neumann, tuttavia possiamo individuare una sequenza di istruzioni macchina esistenti equivalente a tale istruzione mancante. Per esempio, potremmo pensare di caricare una volta per tutte il seguente insieme di valori in memoria:
Questa condizione relativa al "salto indietro" verso il programma principale può essere garantita dalla seguente variante di programma principale, che prima di attivare il sottoprogramma provvede a modificarne il codice inserendo l'indirizzo di ritorno corretto:
Questo modo di organizzare il passaggio dal programma principale al sottoprogramma e viceversa, non é particolarmente comodo da usare, in quanto costringe a conoscere l'indirizzo della cella di memoria corrispondente alla istruzione di ritorno del sottoprogramma (995, nel nostro caso) per consentire l'inserimento da parte del programma principale dell'istruzione di salto col corretto indirizzo di ritorno. Tuttavia permette di richiamare lo stesso sottoprogramma da punti diversi del programma principale, consentendo comunque il ritorno alla esecuzione della istruzione seguente del programma principale.
Esempio: stampa del cubo di un numero letto dall'ingresso
Per verificare il livello di comprensione circa la possibilità di scomporre un programma complesso in una serie di chiamate di procedure predefinite, provate ad organizzare una modifica dell'esempio proposto per il sottoprogramma di calcolo del prodotto secondo il seguente schema di comunicazione delle informazioni. Provate poi a confrontare la vostra soluzione con la soluzione proposta alla fine di questo file.
Usare 3 celle di memoria contigue per la memorizzazione dei due operandi e dell'indirizzo di ritorno. L'indirizzo della prima cella di memoria per la comunicazione viene stabilito dal programma principale e passato al sottoprogramma come valore nel registro accumulatore. Il valore calcolato del prodotto viene scritto dal sottoprogramma nella cella di memoria corrispondente al primo operando.
Dal punto di vista della organizzazione della macchina come composizione di elementi costruttivi, la macchina di Von Neumann soffriva di un gravissimo difetto, che avrebbe impedito l'evoluzione dei sistemi di calcolo così come l'abbiamo conosciuto in questi ultimi anni: la mancanza di modularità. Nella struttura della nostra macchina il comportamento del sistema é completamente determinato dalla Control Unit. Se per esempio volessimo cambiare l'unità di ingresso con un'altra (anche con funzionalità simili ma comandata da segnali di controllo diversi), allora dovremmo modificare più o meno drasticamente anche la Control Unit. Se volessimo aggiungere un secondo dispositivo di uscita, allora dovremmo cambiare (ampliare) l'insieme delle istruzioni della macchina convenzionale.
Per aumentare la modularità di un sistema di calcolo, fin dagli anni '60 venne introdotta una innovazione architetturale fondamentale: la interconnessione di dispositivi mediante bus. Questa connessione é schematizzata nella seguente figura:
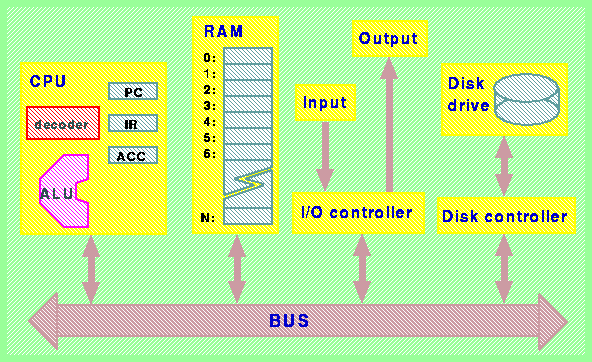
La sua caratteristica principale é quella di svincolare l'unità di controllo (chiamata normalmente CPU, da Central Processing Unit) dagli altri dispositivi.
Ogni dispositivo aggiuntivo (unità di ingresso, di uscita, dischi, ecc.) interagisce autonomamente col resto del sistema mediante un controllore connesso al bus di sistema. Normalmente questi controllori sono a loro volta dispositivi programmabili in grado di accedere alla RAM senza l'intervento della CPU.
L'aggiunta di un nuovo controllore connesso al bus permette quindi di aggiungere dispositivi inizialmente non previsti nel sistema, senza modifiche ai dispositivi esistenti.
Vedremo poi nel seguito del corso come la CPU può programmare i controllori degli altri dispositivi mediante la tecnica dei registri mappati in memoria, e come questi possano usare il bus per accedere alla RAM in competizione con la CPU grazie ad un arbitro per l'uso del bus.
La struttura di interconnessione di tipo bus permette di suddividere il sistema di calcolo in tante unità tra loro indipendenti, ciascuna specializzata per portare avanti un particolare compito (la stampa, la memorizzazione su disco, la comunicazione su una rete di calcolatori).
Tale approccio viene chiamato di decomposizione funzionale. Così come la stratificazione in diversi livelli di astrazione, la decomposizione funzionale può essere efficacemente utilizzata per dominare la complessità intrinseca dei sistemi di calcolo consentendoci di concentrare l'attenzione su una singola funzionalità del sistema stesso.
Notare che stratificazione in diversi livelli di astrazione e decomposizione funzionale sono metodi di "semplificazione" dei problemi tra loro ortogonali (ovvero totalmente indipendenti l'uno dall'altro). Dato un problema complesso possiamo decidere di applicare l'una o l'altra tecnica, o entrambe simultaneamente, secondo la nostra convenienza.
Esempi di uso combinato delle due tecniche portano normalmente alla identificazione di alcune funzionalità di base dei sistemi di calcolo (quali ad esempio il meccanismo delle interruzioni, della memoria virtuale, del multitasking, il file system, la connessione in rete, ecc.) alla cui realizzazione concorrono tecniche, dispositivi e programmi concepiti e realizzati a diversi livelli di astrazione. Ritorneremo ad approfondire queste considerazioni man mano che troveremo esempi di applicazione di questo principio generale.
Provando a scrivere programmi per la nostra macchina di Von Neumann ci siamo resi conto della difficoltà pratica di strutturare il codice in modo da poter per esempio identificare dei sottoprogrammi di utilità generale e preparare delle librerie (pessima trasposizione in italiano del termine inglese program library, che significa biblioteca di programmi).
Dal punto di vista matematico, si può dimostrare formalmente che qualunque funzione calcolabile può essere espressa sotto forma di un programma che faccia uso delle sole istruzioni della nostra macchina di Von Neumann (a parte il problema di utilizzo di una unità di memoria sufficientemente capiente). Quindi potremmo affermare che, in teoria, una macchina di tipo Von Neumann é sufficiente per soddisfare qualsiasi esigenza.
La differenza fondamentale tra il punto di vista di un Matematico ed il punto di vista di un Informatico é che il matematico non ha necessità di usare effettivamente un sistema di calcolo, per cui si accontenta di sapere che una macchina di tipo Von Neumann potrebbe bastare per soddisfare qualsiasi esigenza di calcolo ipotetica. L'informatico é invece la persona che deve usare effettivamente un sistema di calcolo per risolvere problemi concreti, quindi il problema di sapere quanta fatica costa la creazione di un programma e quante risorse (quantità di memoria, tempo di calcolo, ecc.) sono necessarie per portare a termine una computazione diventa rilevante.
Gli informatici hanno sviluppato a partire dagli anni '60 ad oggi delle tecniche di programmazione che fanno normalmente uso di linguaggi ad alto livello, e (giustamente) si rifiutano ormai di programmare in linguaggio macchina. Il criterio principale che viene oggi usato per giudicare la "bontà" di una macchina convenzionale é quindi costituito dal grado di semplicità e di efficienza con cui questa macchina convenzionale consente di riprodurre i costrutti di programmazione presenti nei moderni linguaggi ad alto livello.
Per esempio, tutte le macchine convenzionali moderne offrono dei meccanismi ottimizzati per la soluzione del problema di attivazione di un sottoprogramma, passaggio dei parametri dal programma principale verso il sottoprogramma e ritorno dei risultati dal sottoprogramma al programma principale, e riattivazione del programma principale dal punto in cui era stato interrotto.
Altro punto debole del nostro esempio di macchina di Von Neumann sono le modalità di accesso alla memoria (solo indirizzamento diretto, usando la terminologia che introdurremo più avanti nel corso). Tutte le macchine convenzionali moderne realizzano modalità di accesso più sofisticate, che permettono di evitare completamente la tecnica di automodificazione delle istruzioni del programma. Ciò consente di proteggere le celle di memoria contenenti il codice del programma contro i cambiamenti dei valori memorizzati durante l'esecuzione, offrendo quindi un maggior livello di sicurezza nei confronti di possibili errori di programmazione. Normalmente vengono poi usate tecniche di accesso alla memoria mediante indirizzamento virtuale, che impediscono ad un programma di accedere a celle di memoria senza un esplicito permesso del sistema operativo.
Procedura di moltiplicazione:
Programma principale per prodotto tra due valori letti e stampa del risultato:
Notare che con questa strutturazione il programmatore del programma
principale deve conoscere solo l'entry point (ossia
l'indirizzo della prima istruzione) del sottoprogramma ed il numero
dei parametri di comunicazione (ossia che la procedura richiede 2 operandi
e restituisce un solo risultato che ricopre il primo operando).
La parte di automodificazione del codice viene invece interamente
confinata nel sottoprogramma, riducendo quindi la possibilità
di commettere errori di programmazione.