Scopo di questo capitolo é di arrivare il più rapidamente possibile alla definizione e comprensione dei circuiti sequenziali fondamentali (Registri, Memorie, ecc.) usati come blocchi costruttivi per la realizzazione di microarchitetture.
La trattazione parte a livello di definizione dei principali tipi di flip-flop
mediante interconnessione di funzioni combinatorie elementari.
Verrà evidenziata la differenza concettuale tra circuiti sincroni e asincroni.
Degli aspetti tecnologico/realizzativi verranno citati solo quelli che hanno
un impatto diretto sulla possibilità di ottenere circuiti ad elevatissimo
grado di integrazione (VLSI).
Sono gli elementi base per la costruzione di circuiti sequenziali complessi. Una caratteristica comune di tutti i circuiti sequenziali é quella di basarsi sull'uso di un circuito combinatorio di base, nel quale alcune uscite sono collegate ad alcuni ingressi dello stesso circuito combinatorio. Questo tipo di connessione ciclica tra uscite ed ingressi fa si che i flip-flop possano assumere valori di uscita diversi a parità di valori di ingresso esterno. Tale caratteristica viene usata per ottenere una funzione di "memorizzazione" di valori binari.
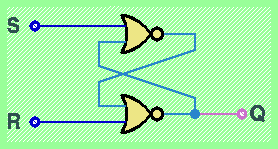
É il tipo più semplice di circuito sequenziale. Una realizzazione in logica NOR é rappresentata in figura:

Non sapendo di aver a che fare con un circuito sequenziale, potremmo provare a studiare il comportamento del circuito illustrato in figura ricavandone la tavola di verità. Questo approccio é applicabile solo per tre delle quattro possibili configurazioni di valori in ingresso:
S R | Q
------+--
0 0 | ?
0 1 | 0
1 0 | 1
1 1 | 0
In particolare il valore di uscita corrispondente alla configurazione di
ingresso S=R=0 non é determinabile a causa della presenza del ciclo
chiuso tra ingressi e uscite delle funzioni.
L'analisi può procedere solo se supponiamo di conoscere già il valore dell'uscita Q quando entrambi gli ingressi assumono il valore 0. Se ipotizziamo Q=0, allora possiamo vedere che questo implica valore 1 in uscita alla funzione NOR in alto, e di conseguenza Q=0, confermando la nostra ipotesi. Ma anche se ipotizziamo Q=1 possiamo concludere che questo implica valore 0 in uscita alla funzione NOR in alto, e di conseguenza Q=1, confermando nuovamente la nostra ipotesi di partenza. Troviamo quindi un caso in cui la soluzione al problema di trovare il valore di uscita non é unica: entrambe le soluzioni Q=0 e Q=1 sono ammissibili con la configurazione di ingresso S=R=0.
Come possiamo arrivare a determinare il valore in uscita nel caso in cui entrambi i valori booleani sono soluzioni ammissibili? La risposta consiste nel considerare sequenze di configurazioni diverse, facendo variare nel tempo il valore delle variabili di ingresso.
Supponiamo di partire dalla configurazione S=1 ed R=0, e di cambiare poi il valore di S portandolo a 0. Siccome le nostre funzioni NOR saranno realizzate mediante dispositivi fisici, possiamo pensare che qualsiasi realizzazione del nostro flip-flop sarà sempre soggetta ad una certa "inerzia" dei valori di uscita rispetto a cambiamenti dei valori di ingresso. Osservando il comportamento del flip-flop con una scala dei tempi sufficientemente fine potremo sempre individuare un intervallo di tempo non nullo durante il quale i valori di uscita non cambiano nonostante una variazione dei valori di ingresso sia già avvenuta. Nel nostro caso specifico, riusciremo sempre ad individuare un intervallo di tempo finito durante il quale il valore dell'uscita Q continua ad essere 1 anche dopo che il valore della variabile di ingresso S é diventato 0; durante tale intervallo di tempo la funzione OR in alto continua a produrre il valore di uscita 0, che conferma il valore Q=1 in uscita alla funzione NOR in basso. Quindi, per una forma di continuità dei valori in uscita alle funzioni a seguito di variazioni dei valori in ingresso, possiamo affermare con certezza che Q deve continuare ad assumere sempre il valore 1 anche dopo che l'ingresso S ha assunto il valore 0.
In modo del tutto analogo possiamo arrivare alla conclusione che se la configurazione di ingresso S=R=0 é preceduta nel tempo dalla configurazione S=0 ed R=1 (che forza in uscita il valore Q=0 senza ambiguità), allora in uscita troveremo sicuramente il valore Q=0.
Possiamo quindi toccare con mano una proprietà che distingue nettamente i circuiti sequenziali dai circuiti combinatori: in un circuito combinatorio il valore delle uscite é univocamente determinato dai valori attuali delle variabili di ingresso (a meno di un piccolo ritardo dovuto all'inerzia di assestamento dei dispositivi fisici che realizzano le funzioni); in un circuito sequenziale, il valore delle uscite può dipendere, oltre che dai valori attuali, anche dalla sequenza dei valori precedenti delle variabili di ingresso.
Notiamo infine che la configurazione di ingresso S=R=1 é anomala dal punto di vista di uso del circuito sequenziale: la sequenza S=R=1 seguito da S=R=0 non determina univocamente il valore dell'uscita Q (in alcuni casi potrebbe generare delle oscillazioni periodiche tra i valori Q=0 e Q=1, con un periodo determinato dal tempo di assestamento dei dispositivi che realizzano le funzioni NOR). Per questo la configurazione di ingresso S=R=1 non viene normalmente utilizzata.
Un flip-flop di tipo SR può essere usato, come abbiamo visto, per memorizzare un bit di informazione mediante l'uso di opportune sequenze di valori di ingresso. Tuttavia queste operazioni di memorizzazione risultano macchinose da gestire in termini di variazioni di variabili di ingresso. Vediamo quindi come sia possibile semplificare l'operazione di memorizzazione mediante l'interposizione di un semplice circuito combinatorio all'ingresso:
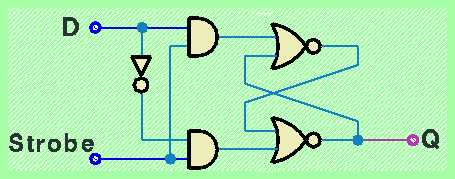
Questa variazione viene denominata flip-flop tipo D, oppure "latch".
L'introduzione delle due funzioni AND e della funzione NOT impedisce il manifestarsi della configurazione proibita S=R=1 per il flip-flop. L'ingresso Strobe determina l'operazione di memorizzazione: quando Strobe=0 gli ingressi S e R del flip-flop assumono il valore 0, determinando il mantenimento del valore di uscita Q precedentemente memorizzato; quando Strobe=1, gli ingressi del flip-flop assumo i valori S=D e R=¬D, comportando quindi la memorizzazione del valore in ingresso D sull'uscita Q. Notare quindi che l'uscita Q può cambiare di valore solo quando l'ingresso Strobe assume il valore 1; l'uscita invece rimane costante quando Strobe=0, indipendentemente da ogni possibile variazione del valore di ingresso D.
Notare che la memorizzazione di un valore nel dispositivo richiede che quel valore venga mantenuto fisso sull'ingresso D per tutto il tempo necessario a passare da Strobe=0 (condizione di riposo) a Strobe=1 (memorizzazione attivata), e poi di nuovo a Strobe=0 (mantenimento del valore memorizzato). Questo modo di funzionamento può essere posto in analogia con lo scatto di una fotografia di tipo "ritratto", dove il soggetto deve rimanere fermo in posa per tutta la durata dell'operazione. Lo scatto di una fotografia "istantanea" di un soggetto in movimento richiede invece l'uso di un otturatore con tempo di scatto molto piccolo rispetto alla velocità di movimento del soggetto. Vediamo qui di seguito come realizzare un dispositivo di memorizzazione capace di "campionare" in un certo istante il valore di una variabile eventualmente soggetta a variazioni.
In figura é illustrata una configurazione Master/Slave per il flip-flop di tipo D.

A prezzo di un raddoppio della complessità circuitale del dispositivo (rispetto al Latch del paragrafo precedente) si ottiene l'effetto "otturatore" che permette di rendere estremamente veloce il tempo di campionamento del valore di ingresso D. Quando l'ingresso Ck (clock) assume stabilmente il valore 0, il primo flip-flop a sinistra (Master) risulta essere bloccato sulla memorizzazione del valore precedente, mentre il secondo flip-flop a destra (Slave) riproduce tale valore in uscita (a causa dell'inversione del segnale di controllo in ingresso alle funzioni AND). Se poi l'ingresso Ck commuta sul valore 1, allora le parti si invertono, e sarà il flip-flop Slave a rimanere bloccato nella posizione di memorizzazione del valore precedente, mentre il flip-flop Master riproduce l'attuale valore presente sull'ingresso D (ma senza effetto sul valore delle uscite). Solo nell'istante della commutazione da 1 a 0 della variabile di controllo Ck il valore corrente dell'ingresso D verrà memorizzato sul flip-flop Master e riprodotto sull'uscita dal flip-flop Slave.
Vediamo quindi come la configurazione Master/Slave permette di realizzare un tipo di comportamento che, per quanto riguarda i cambiamenti di valori sulle uscite, dipende non dal valore della variabile di controllo (level-triggered), bensì dalla variazione di tale valore (edge-triggered). In forma sintetica (ossia prescindendo dalla sua realizzazione interna come combinazione di funzioni logiche elementari) un Flip-Flop di tipo Master/Slave Edge-triggered viene rappresentato come in figura:
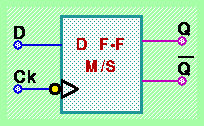
Il "triangolino" all'interno del rettangolo in corrispondenza dell'ingresso "Ck" simboleggia il comportamento "edge-triggered" del dispositivo, mentre il "pallino di negazione" fuori dal rettangolo sull'ingresso "Ck" indica la commutazione dell'uscita in corrispondenza del "fronte di discesa da 1 a 0" dell'ingresso "Ck" (un D F-F sensibile ai "fronti di salita da 0 a 1" viene invece rappresentato come sopra, ma senza il "pallino di negazione" sull'ingresso "Ck").
Notiamo in oltre come solo le variazioni dell'ingresso Ck possono produrre delle variazioni del valore delle uscite. Variazioni dell'altra variabile di ingresso, pur concorrendo a determinare il prossimo valore in uscita, non possono influire sul valore corrente, che viene mantenuto stabile fino alla prossima variazione significativa dell'ingresso Ck. Un circuito sequenziale con queste caratteristiche viene detto sincrono. Per contro, un circuito sequenziale nel quale le variazioni di più di una variabile di ingresso possono determinare immediatamente (a meno del ritardo di propagazione dei valori tra ingresso ed uscita delle funzioni) variazioni dei valori in uscita vengono detti asincroni. Per esempio, i flip-flop di tipo Set/Reset e di tipo Latch sono da considerarsi asincroni.
Nella seguente figura é riportata una varizione sul tema dei flip-flop Master/Slave (sincroni), chiamata flip-flop tipo T:
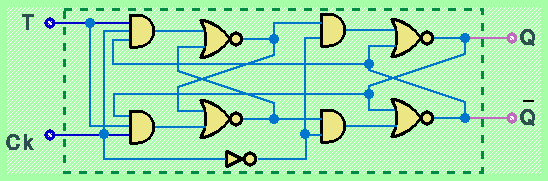
La presenza della connessione tra uscite dello Slave e ingressi del Master fa si che il dispositivo sia in grado di effettuare una commutazione del valore quando l'ingresso T é posto al valore 1 ed il segnale di clock viene variato. L'uscita rimane invece invariata se l'ingresso T assume il valore 0 durante il periodo di tempo in cui varia il valore del segnale di clock.
Separando i due ingressi delle funzioni AND del dispositivo Master si ottiene la configurazione chiamata J-K:
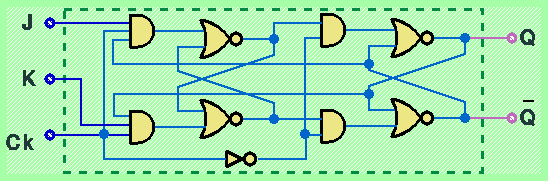
La connessione J-K rappresenta il tipo più generale di flip-flop Master/Slave (sincrono), in grado di esibire i seguenti comportamenti:
J K Ck | Q ¬Q
------------+--------
0 0 1->0 | Q ¬Q
0 1 1->0 | 0 1
1 0 1->0 | 1 0
1 1 1->0 | ¬Q Q
In un certo senso, il flip-flop J-K può essere interpretato come
la versione sincrona del flip-flop Set/Reset, almeno per quanto riguarda
le prime tre combinazioni di ingressi elencati nella tabella.
A questi si aggiunge il comportamento di inversione del valore
precedentemente memorizzato, tipico di un dispositivo sequenziale sincrono.
Cerchiamo di ragionare in termini più generali rispetto agli esempi di flip-flop visti fin'ora. L'idea di base per arrivare a produrre un dispositivo sequenziale é di collegare alcune uscite di un circuito combinatorio con ingressi dello stesso circuito in modo da produrre dei cicli chiusi (vedi schema generale in figura):
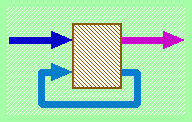
Naturalmente, l'esistenza di cicli chiusi nella rappresentazione grafica del dispositivo in termini di funzioni elementari é una condizione necessaria ma non sufficiente per produrre dei circuiti sequenziali (tantomeno dei circuiti sequenziali "utili").
A tale schema di principio può essere ricondoto qualsiasi circuito sequenziale, sia asincrono che sincrono.
Ricordiamo la definizione di circuito sequenziale sincrono: un circuito sequenziale tale per cui solo variazioni di una variabile di controllo (chiamata di solito clock) possono comportare variazioni dei valori di uscita; il cambiamento di valore di qualsiasi altra variabile di ingresso non determina immediatamente alcun cambiamento dei valori di uscita. Ogni circuito sequenziale che non soddisfa la definizione di circuito sincrono viene chiamato asincrono.
nella quale il ciclo viene chiuso mediante dei dispositivi del tipo flip-flop Master/Slave edge-triggered. Vediamo quali vantaggi porta l'utilizzazione di circuiti sincroni rispetto a quella dei circuiti asincroni, a fronte della maggior complessità di realizzazione.
Consideriamo l'esempio di circuito sequenziale asincrono illustrato in figura:

Supponiamo di voler determinare il valore dell'uscita u dopo aver applicato sugli ingressi la seguente sequenza di combinazioni di valori:
config. : 1 : 2 : 3
--------+-----+------+-----
d = 1 : 0 : 0
c = 1 : 1 : 0
b = 1 : 1 : 1
a = 1 : 1 : 1
Dalla tavola di verità delle funzioni combinatorie e dalla descrizione
del flip-flop Set/Reset determiniamo che la prima configurazione memorizza
il valore u=1. La seconda configurazione consente al flip-flop di mantenere
il valore precedentemente memorizzato, così come la terza.
Quindi possiamo dedurre che il valore prodotto in uscita dall'applicazione
della sequenza di ingressi considerata sia u=1.
Non soddisfatti di questa risposta, proviamo ora a considerare alcuni dettagli realizzativi del dispositivo Multiplexer. Supponendo di considerare la realizzazione minimale del multiplexer vista in precedenza mediante un NOT, due AND ed un OR, possiamo ipotizzare che ciascuna funzione logica elementare sia caratterizzata da un ritardo di una unità di tempo per produrre il corretto valore di uscita a fronte di una variazione dei valori di ingresso. Il passaggio dalla seconda alla terza configurazione della sequenza può quindi essere decomposto in passi elementari di durata pari ad una unità di tempo:
Questo esempio ci mostra come possa essere difficile prevedere il risultato in uscita di un circuito sequenziale asincrono a seguito di variazioni delle configurazioni in ingresso. In particolare vediamo come anche alee molto brevi possono determinare la commutazione permanente di un flip-flop rispetto al valore di uscita previsto basandosi sulla specifica del circuito combinatorio data sotto forma di tavola di verità (prescindendo quindi dalle temporizzazioni delle funzioni).
Il problema di "imprevisti" dovuti ad alee di commutazione può essere completamente eliminato in circuiti di tipo sequenziale sincrono mediante un'opportuna utilizzazione della variabile di controllo clock.
L'uso di dispositivi Master/Slave consente di far variare i valori di ingresso al flip-flop senza per questo alterare il valore delle uscite, fin quando non venga dato un apposito impulso alla variabile di controllo clock. Scegliendo un periodo di variazione per la variabile clock grande rispetto al tempo di assestamento dei valori in uscita del circuito combinatorio a seguito di variazioni dei valori di ingresso, si può quindi ovviare in modo semplice al problema delle eventuali alee di commutazione: queste saranno esaurite nel momento in cui, tramite variazioni della variabile clock, comandiamo il passaggio dallo stato corrente allo stato successivo.
La progettazione di un circuito sincrono può quindi essere basata
sulla specifica del comportamento di un circuito combinatorio basato sulla
tavola di verità, senza necessità di una analisi raffinata del
comportamento in funzione del tempo.
Le uscite dei dispositivi Master/Slave tengono fisso il valore dello stato
corrente, mentre gli ingressi di tali dispositivi predispongono il calcolo
dello stato successivo.
Il passaggio dallo stato corrente allo stato successivo avviene in modo
"istantaneo" e simultaneo per tutti i flip-flop Master/Slave inclusi nel
circuito sincrono a seguito di un impulso della variabile di controllo clock.
I circuiti sequenziali sincroni sono, insieme ai circuiti combinatori, i "mattoni" elementari piu' usati per definire la microarchitettura di un sistema di calcolo moderno. Data la loro potenziale insensibilità alle alee di commutazione dei circuiti combinatori, la loro utilizzazione consente di arrivare a progettare sistemi complessi in modo estremamente semplice e modulare, tenendo conto solo della funzione tra ingresso ed uscita dei dispositivi (e verificando semplici disuguaglianze per quanto riguarda i tempi di assestamento dei valori in ingresso ed in uscita). Normalmente i circuiti sequenziali sincroni vengono classificati in "registri" (contenenti rappresentazioni binarie di dati su uno o più bit) caratterizzati da diverse modalità di manipolazione dei dati.
Rappresentano il tipo più semplice di circuito sequenziale sincrono. Offrono la funzionalità di memorizzazione (per un tempo indefinito) di una combinazione di valori binari. Sono realizzati connettendo uno o più Flip-flop di tipo D Master-Slave in modo che tutti i loro ingressi "Ck" siano comandati dalle variazioni di una sola variabile di ingresso "Clock". Nella seguente figura viene riportato lo schema di realizzazione di un registro "tipo D" a 4 bit, basato sull'uso di 4 Flip-Flop di tipo D M/S:
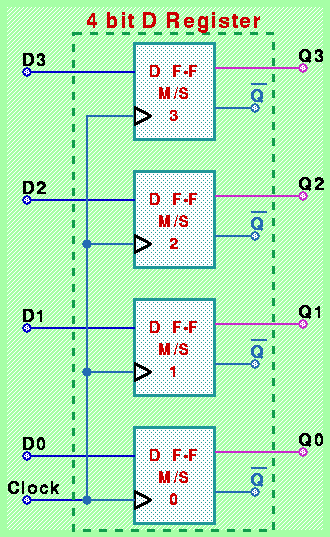
Notare come il nostro registro D rientri perfettamente nello schema generale di circuito sincrono considerando il caso particolare di circuito combinatorio in ingresso che riporta gli ingressi invariati ai flip-flop e di circuito combinatorio di uscita ridotto alla funzione identità.
Il nostro registro D offre le seguenti funzioni:
Passiamo ora a considerare un tipo di registro più sofisticato, in grado di "incrementare di 1" la rappresentazione binaria del numero in esso memorizzato. Tale funzionalità viene ottenuta mediante l'uso di Flip-Flop T M/S. Consideriamo l'esempio di registro contatore a 4 bit illustrato in figura:
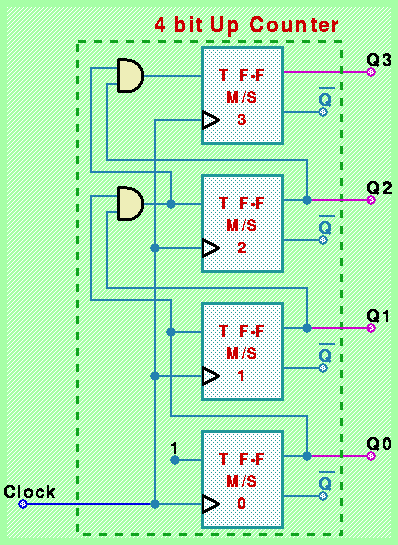
Supponiamo che "magicamente" il nostro registro assuma il valore zero nel momento che noi cominciamo ad osservarne il comportamento (ossia che tutti e 4 i flip-flop riportino la cifra "0" sulla propria uscita "Qi"). Ad ogni fronte di salita "0 -> 1" applicato all'ingresso "Clock" corrisponde una commutazione del F-F in basso (il numero zero) dovuta al fatto che il suo ingresso "T" é connesso al valore costante "1". Poichè l'uscita "Q0" corrisponde alla cifra meno significativa della rappresentazione binaria, questo corrisponde al passaggio dalla rappresentazione di un numero pari a quella di un numero dispari, o viceversa.
Notiamo in oltre come la condizione di commutazione per la i-esima cifra corrisponde al riporto non nullo nel caso di somma della costante uno col valore precedentemente memorizzato. Come già visto in precedenza per il dispositivo che realizza il carry lookahead nel caso di un dispositivo incrementatore, tale condizione si riduce al calcolo della funzione AND di tutte le cifre meno significative. Tale funzione può essere realizzata sia in forma modulare come illustrato in figura, oppure con un solo livello di logica mediante l'uso di funzioni AND con numero di ingressi crescente all'aumentare dell'ordine della cifra (ossia Ti = Q(i-1) · Q(i-2) · ... · Q0). Tale variante, pur essendo più costosa da realizzare, presenta il vantaggio di richiedere un tempo di assestamento dei valori sugli ingressi T a seguito di una commutazione costante, indipendentemente dal numero di cifre di rappresentazione del registro. La realizzazione modulare in figura (così come il circuito sommatore con ripple carry), pur essendo più semplice e meno costosa (soprattutto per registri con tanti bit), presenta lo svantaggio di richiedere un tempo di assestamento dei valori sugli ingressi T che cresce linearmente col numero di bit N del registro.
Il tempo di assestamento dei valori in ingresso ai Flip-Flop ha un effetto indiretto sulla velocità di operazione dei dispositivi. Infatti, per garantire il corretto funzionamento di un circuito sequenziale sincrono é necessario porre un vincolo superiore alla velocità di variazione della variabile di controllo Clock: un periodo di tempo intercorrente tra due fronti di salita consecutivi (passaggi consecutivi 0 -> 1) deve essere superiore al tempo di assestamento dei valori in ingresso (T nel nostro caso) a seguito delle variazioni delle uscite (Q nel nostro esempio). Se tale vincolo non fosse rispettato, la sequenza dei valori prodotti dal registro potrebbe non corrispondere alla sequenza dei valori consecutivi ("0000" -> "0001" -> "0010" -> "0011" -> ...). Quindi, in generale, la velocità dei circuiti combinatori connessi nel ciclo tra uscite ed ingressi dei F-F M/S determina (insieme alla velocità dei F-F stessi) la massima frequenza di variazione del Clock che garantisce il funzionamento corretto del dispositivo.
Supponiamo ora di voler aggiungere al nostro registro contatore la possibilità di inserire il valore iniziale 0, indipendentemente dal valore precedentemente memorizzato (operazione di Reset). Mantenendo il vincolo di usare flip-flop di tipo T, dovremmo identificare un circuito combinatorio per produrre il valore di T tale che il flip-flop commuti (T=1) quando il valore memorizzato é diverso da zero (Q=1), e non commuti (T=0) quando il valore memorizzato é già uguale a zero (Q=0). Risulta evidente, quindi, che per ottenere l'azzeramento di tutti i flip-flop che costituiscono il registro basta riportare sull'ingresso T di ciascuno il valore attualmente in uscita Q. Volendo quindi realizzare un registro contatore in grado, ad ogni ciclo di clock, di incrementare il valore precedente di una unità oppure di ripristinare il valore 0, potremmo usare un multiplexer a due ingressi comandato da un bit di controllo per connettere alternativamente agli ingressi T dei flip-flop o la loro uscita Q oppure l'uscita della funzione And tra tutte le uscite Q dei flip-flop che realizzano i bit di ordine inferiore.
Registri costituiti da flip-flop di tipo T si prestano a realizzare funzioni di conteggio diverse dall'incremento di uno per ogni ciclo di clock. Per esempio, possiamo facilmente individuare la condizione di commutazione di un flip-flop per realizzare l'operazione di "decremento di 1" ad ogni ciclo di clock: quando tutti i flip-flop che realizzano i bit di ordine inferiore assumono il valore zero. Consideriamo l'esempio di registro contatore a 3 bit illustrato in figura:
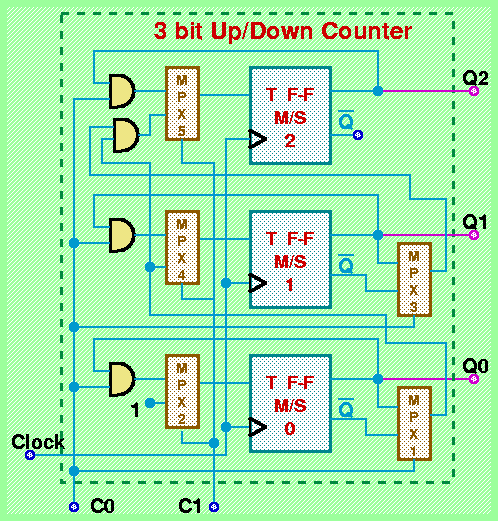
In questo caso, a seconda della combinazione dei due ingressi di controllo C1 e C2, l'occorrenza di una transizione da 0 a 1 del segnale di Clock determina uno tra quattro comportamenti diversi:
Un registro a scorrimento viene realizzato interponendo un multiplexer sugli ingressi di un registro di tipo D, come illustrato in figura nel caso di un registro a 4 bit:
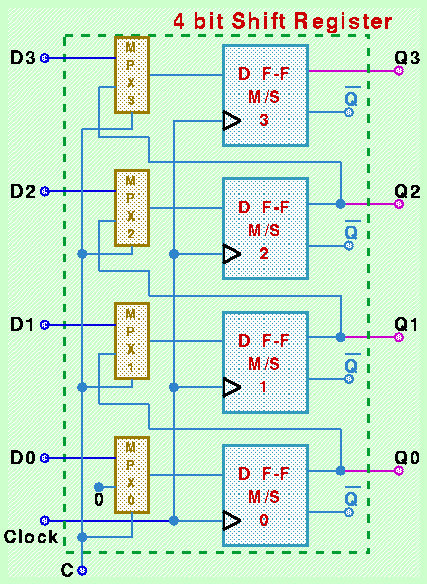
A seconda del valore della variabile di controllo C, ad ogni ciclo di clock il registro realizza una delle seguenti due funzionalità:
L'utilizzazione principale di un registro a scorrimento consiste nella
cosiddetta conversione "parallelo/seriale" e viceversa "seriale/parallelo".
In particolare l'esempio illustrato in figura potrebbe essere impiegato
per memorizzare un dato espresso in forma binaria su 4 bit (primo ciclo
di clock con valore C=1), e poi trasmettere uno alla volta i bit della
rappresentazione su un unico filo (l'uscita Q3) durante i 4 successivi
cicli di clock (con ingresso di controllo C=0).
Passiamo ora ad esiminare il problema di realizzazione di moduli di memoria di tipo RAM, ossia caratterizzati dalla presenza di un congruo numero di celle identificate da un numero (detto indirizzo), ciascuna di queste in grado di contenere informazioni codificate in un formato fisso di rappresentazione su N bit. Deve essere possibile accedere individualmente ad una qualunque cella di RAM (specificandone l'indirizzo in forma binaria) per una operazione di inserzione di un valore (scrittura) oppure di estrazione del valore precedentemente memorizzato (lettura). Ogni cella di RAM deve poi mantenere l'ultimo valore inserito fino al momento in cui non viene inserito un altro valore diverso nella stessa cella (ossia usando lo stesso indirizzo). Quindi le operazioni di lettura devono essere di tipo "non distruttivo", ossia non devono minimamente alterare la capacità del dispositivo di mantenere memoria dello stesso valore anche dopo la lettura.
Avendo già visto la realizzazione di registri di tipo D atti a memorizzare configurazioni di N bit, possiamo pensare di adottare molte copie di tali registri per la realizzazione delle singole celle di memoria. Questo approccio porta alla definizione di dispositivi chiamati RAM statiche. L'unica difficoltà di principio che dobbiamo superare per definire la struttura di un dispositivo di tipo RAM statica é quella di realizzare un meccanismo che consenta l'accesso in lettura e/o scrittura ad una sola cella alla volta, designata dall'indirizzo proveniente dall'esterno sotto forma di rappresentazione binaria su K bit.
Consideriamo separatamente le operazioni di lettura e scrittura di celle di memoria RAM, ed iniziamo a preoccuparci della realizzazione della operazione di lettura. Nel caso di un singolo registro di tipo D, il dato memorizzato é sempre disponibile sui fili di uscita Q dei flip-flop, quindi la "lettura" non richiede alcuno sforzo o supporto particolare: basta semplicemente osservare i valori presenti sui fili di uscita del dispositivo. Nel caso di un dispositivo RAM, invece, occorre connettere sui fili di uscita del dispositivo i fili di uscita di un solo registro di tipo D (fra i tanti che sono presenti nel modulo RAM), in particolare quello individuato dalla rappresentazione binaria su K bit dei fili di ingresso che codificano l'indirizzo della cella da leggere. Non é difficile arrivare quindi a concludere che occorre interporre un dispositivo di tipo Multiplexer con 2**K ingressi e una uscita (comandato dai K fili di indirizzo); ciascun ingresso e l'uscita dovranno essere costituiti da un insieme di N fili, in modo da poter connettere la rappresentazione della cella desiderata sulla uscita del modulo RAM. In figura é illustrata la realizzazione mediante un multiplexer di uscita della lettura di una cella di memoria nel caso di un modulo RAM statica costituito da 4 celle di 8 bit ciascuna.
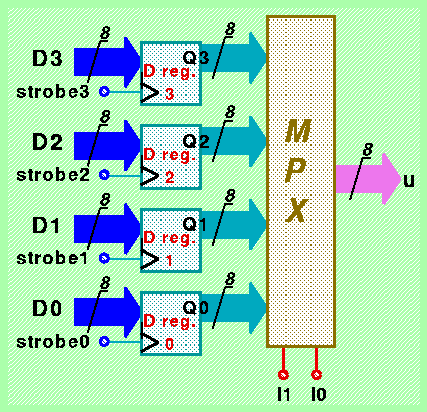
Se consideriamo invece il problema della memorizzazione in una sola cella di memoria dei dati presenti sull'ingresso del modulo RAM, dovrebbe essere evidente che questo problema può essere risolto "smistando" un segnale di "strobe" ad uno e uno solo dei registri di tipo D (mentre tutti gli altri devono continuare a ricevere il valore 0 sul loro ingresso strobe). Il modo più semplice di realizzare tale funzionalità consiste quindi nell'adozione di un demultiplexer comandato dai fili di indirizzamento per la connessione dell'ingresso strobe del modulo agli ingressi strobe dei singoli registri che realizzano le diverse celle di memoria. Gli ingressi D dei registri possono invece essere collegati tutti in parallelo, come indicato nella seguente figura (sempre per il caso particolare di 4 celle da 8 bit ciascuna):
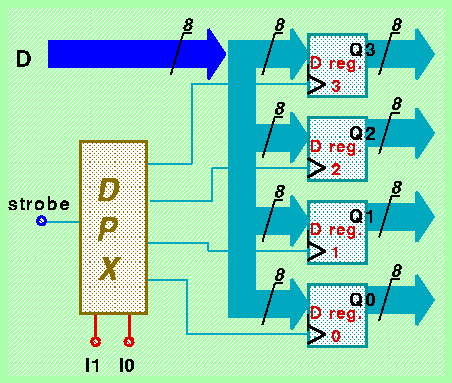
Utilizzando un multiplexer ed un demultiplexer separati ed alimentati da due insiemi diversi di fili di indirizzamento, potremmo produrre un dispositivo RAM in grado di operare simultaneamente in lettura su una cella ed in scrittura su un'altra cella. Normalmente non si richiede una tale funzionalità, per cui si conviene di usare un solo insieme di fili di indirizzamento. A questo punto si può pensare di economizzare sulla realizzazione del modulo RAM mettendo in comune il dispositivo di tipo Decoder che si trova "nascosto" nel multiplexer e nel demultiplexer. Lo schema di realizzazione ottimizzato del modulo RAM diventerà quindi quello illustrato in figura nel caso di 4 celle da 2 bit ciascuna:
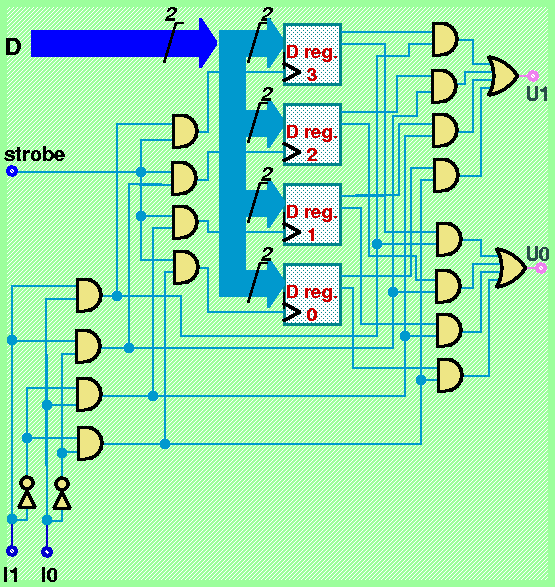
La memorizzazione avviene mandando un impulso sull'ingresso strobe del modulo RAM dopo aver predisposto il valore da memorizzare sugli ingressi D. La lettura avviene sempre, senza bisogno di segnali particolari di controllo oltre alla specifica dell'indirizzo. Quindi, in particolare, la lettura può ancora avvenire simultaneamente alla scrittura, questa volta però col vincolo che si può leggere solo il contenuto della cella che viene indirizzata anche per l'operazione di scrittura. Anche questa possibilità di lettura e scrittura simultanea della stessa cella non viene normalmente ritenuta utile nel caso della memoria RAM di un sistema di calcolo, per cui si preferisce adottare delle soluzioni circuitalmente più semplici che non supportano tale funzionalità.
Il modo più semplice ed economico per realizzare delle memorie RAM adatte all'inserimento in sistemi di calcolo é quello di definire dei moduli standardizzati, ciascuno dei quali in grado di implementare un "pezzo" della RAM richiesta all'interno del sistema, e strutturati in modo tale per cui l'utente debba semplicemente preoccuparsi di comprarne un numero adeguato per soddisfare le sue esigenze, potendoli poi connettere nel modo più semplice possibile, ossia attaccandoli tutti sugli stessi fili di inidirizzamento e di trasporto dei dati. Il criterio di acquisizione e assemblaggio dei moduli RAM standardizzati é quindi legato esclusivamente alla quantità di memoria RAM che si vuole inserire all'interno del sistema.
Cominciamo quindi col definire le unità di misura utilizzate per quantificare la disponibilità di memoria. L'unità di misura elementare é il bit (binary digit), ossia una singola cifra binaria. A differenza di altre quantità fisiche, non ha senso pensare a delle frazioni più piccole di informazione, in quanto la possibilità di differenziare tra due soli simboli é il primo passo a partire dall'informazione nulla (che può essere immaginata come la rappresentazione di un valore costante, che tutti conoscono già, senza nessun bisogno di dover ricorrere all'uso di un dispositivo RAM per ricordarselo). Vengono poi definiti dei multipli in termini di potenze di due. Un byte viene definito come un sinonimo per indicare 8 bit. Vengono poi definiti i coefficenti moltiplicativi:
1 K (=1024, ossia 210), pronunciato "un cappa"
1 M (=1048576, ossia 220), pronunciato "un mega"
1 G (=1073741824, ossia 230), pronunciato "un giga"
1 T (=1099511627776, ossia 240), pronunciato "un tera"
Tali coefficenti moltiplicativi possono essere applicati sia ai bit (che abbrevieremo con "b" minuscola) sia ai byte (che abbrevieremo con "B" maiuscola). Per esempio, diremo 24Kb (ventiquattro cappa bit) per indicare 24576 bit, oppure 3KB (tre cappa byte) per indicare lo stesso numero di bit in modo perfettamente equivalente.
Supponiamo per esempio di aver definito dei moduli RAM standardizzati da 4MB (ossia 33554432 bit), organizzati come 1M celle (ossia 1048576 celle) da 32 bit ciascuna (ovvero da 4 byte). A questo punto noi vorremmo poter comprare un qualunque numero di questi moduli (uno, due o sei, per esempio), per assemblare sistemi con quantità totale di memoria diversa (4MB, 8MB oppure 24MB, rispettivamente), sempre mantenendo l'organizzazione delle informazioni in celle da 4B, quindi aumentando semplicemente il numero di celle di RAM globalmente utilizzabili nel nostro sistema di calcolo. Una tale organizzazione dei moduli di memoria (che é quella adottata nei sistemi di calcolo moderni) può essere realizzata stabilendo a priori un numero massimo di celle di memoria assemblabile in un sistema (molto) superiore a quello effettivamente contenuto in un singolo modulo. Per esempio, potremmo pensare di definire la possibilità di connettere fino ad un massimo di 16 dei nostri moduli standardizzati, arrivando quindi a comporre una RAM da 64MB. Dividendo la dimensione massima realizzabile della RAM per la capacità di una singola cella di memoria otteniamo il numero massimo di celle di memoria che potranno essere contenute nel nostro sistema, e quindi il numero di fili di indirizzamento che dovrà essere utilizzato. Nel nostro caso, otteniamo 64MB/4B= 16M celle, e quindi calcoliamo il numero di fili di indirizzamento necessari come logaritmo in base 2 di tale numero di celle (24 fili in questo caso). D'altra parte, ciascun modulo conterrà solo 1M celle, quindi avrà bisogno di soli 20 fili di indirizzamento connessi al proprio decoder per la scelta della cella da connettere in uscita o sull'impulso di memorizzazione. I rimanenti quattro fili di indirizzamento verranno usati per attivare al più un modulo standard tra quelli presenti all'interno del sistema per ogni indirizzo. Questa selezione di un solo modulo può essere ottenuta dotando ciascun modulo di un circuito comparatore di uguaglianza del tipo illustrato in precedenza per confrontare i 4 bit più significativi dell'indirizzo con un valore costante assegnato univocamente a ciascun modulo nel momento della sua inserzione all'interno di un sistema. Il modo più semplice di assegnare tale costante a ciascun modulo (ancorchè non "plug-and-play") consiste nell'usare dei commutatori azionati manualmente, mediante i quali l'utilizzatore seleziona l'insieme di indirizzi ai quali deve "rispondere" ciascun modulo prima di inserirlo effettivamente nel sistema; sarà quindi cura dell'utilizzatore, in questo caso, di evitare i casi di "omonimia" tra piu' moduli inseriti nello stesso sistema.
Al fine di poter effettivamente connettere piu' moduli in parallelo nello stesso sistema occorre ancora risolvere il problema di coordinare tante uscite provenienti da più moduli diversi utilizzando gli stessi fili per il trasporto dei dati. Tale interconnessione detta di tipo "bus" richiede l'adozione di dispositivi particolari detti "a tre stati" di uscita.
Cominciamo a considerare il problema generico di voler connettere due uscite di circuiti logici allo stesso filo, in modo da raccogliere l'uscita da uno di questi e portarla in ingresso a qualche altro dispositivo. Una tale connessione non é fisicamente realizzabile usando una normale logica a 2 livelli come quella considerata fino ad ora. Infatti sorgerebbero dei problemi di "conflitto" tra le due uscite qualora queste corrispondessero a valori diversi tra loro (ossia una uscita a "0" e l'altra a "1"). Le uscite potrebbero essere connesse solo se fossimo certi che i due dispositivi producono sempre lo stesso valore di uscita, in modo che il valore sia univocamente determinato ed i dispositivi non rischino di essere danneggiati. Nel caso in cui i due dispositivi producessero valori diversi, potremmo stabilire cosa succede solo conoscendo i dettagli di realizzazione dei dispositivi (ossia il livello -1 della nostra classificazione). Conoscendo i parametri elettrici dei transistor usati per la realizzazione potremmo stabilire se il valore sul filo é "0" oppure "1" e se i dispositivi possono essere danneggiati oppure no da questa connessione anomala.
La soluzione del problema viene ottenuta adottando dei dispositivi particolari chiamati "a tre stati di uscita", i quali possono produrre oltre ai valori "0" e "1" anche un terzo valore detto "non connesso". Una uscita di un dispositivo a tre stati che produce il valore "non connesso" si comporta come se la sua uscita non fosse collegata al filo, permettendo quindi ad un altro dispositivo di produrre indisturbato il valore "0" oppure "1" sullo stesso filo. Un tale dispositivo viene normalmente realizzato con 2 ingressi binari ed una uscita a tre stati e rappresentato graficamente da un triangolo, come illustrato in figura:
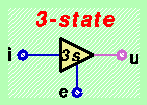
Il funzionamento di un tale dispositivo viene definito mediante la seguente "tavola di verità":
3-state: i e | u ------+-------- 0 0 | non connesso 0 1 | 0 1 0 | non connesso 1 1 | 1Due o più uscite a tre stati possono essere connesse sullo stesso filo a patto di poter garantire che al massimo uno dei dispositivi 3-s sia pilotato col valore 1 sull'ingresso "e". Se tale condizione é rispettata, allora non si manifesteranno mai situazioni di conflitto nelle quali due dispositivi "vogliono produrre" valori diversi sullo stesso filo contemporaneamente.
Una connessione di tipo "bus" realizzata collegando più uscite 3-s allo stesso filo deve garantire la condizione di assenza di conflitti tra due o più uscite mediante l'adozione di un opportuno protocollo per il coordinamento della connessione delle uscite stesse. Nel caso di moduli di tipo RAM tale protocollo viene realizzato a livello circuitale utilizzando due variabili binarie di controllo per le operazioni della RAM, chiamate normalmente "CS" e "R/nW". Il significato dei valori assunti dalle due variabili di controllo é il seguente: CS=0 significa "il modulo non deve essere attivato", ed in questo caso il valore assunto dalla variabile "R/nW" é irrilevante; CS=1 significa "il modulo deve attivarsi per una operazione di lettura o di scrittura", ed in questo caso il valore assunto dalla variabile "R/nW" indica il tipo di operazione richiesta (R/nW=1 significa "lettura", R/nW=0 significa "scrittura"). In figura é illustrato un ulteriore circuito combinatorio di decodifica delle variabili CS ed R/nW per realizzare le operazioni di lettura e scrittura secondo il protocollo specificato, sempre nel caso di 4 celle da 2 bit.
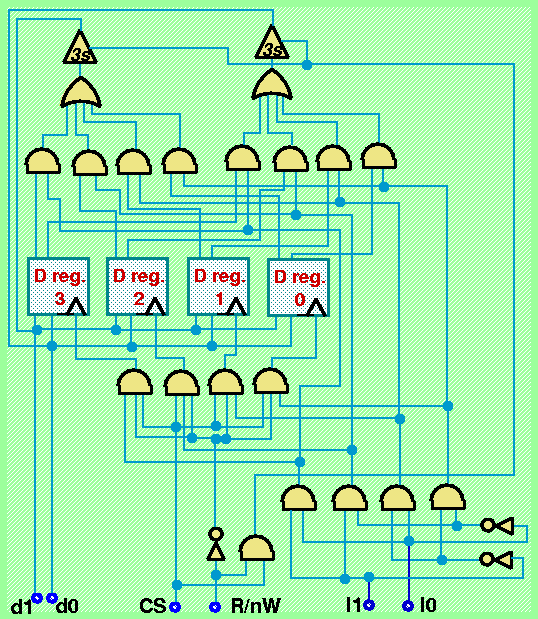
L'uso di dispositivi a 3 stati e la specifica di realizzare alternativamente operazioni di lettura o di scrittura consente di usare gli stessi fili "d0" e "d1" per portare i dati sia in ingresso al modulo (operazione di scrittura) sia in uscita dal modulo (operazione di lettura). In ogni caso il modulo collegherà la "sua" uscita ai fili solo a seguito della combinazione di valori di controllo CS=1 e R/nW=1, ossia solo quando il modulo stesso viene "interrogato" per conoscere il contenuto di una delle sue celle (il cui indirizzo é specificato sui fili di indirizzamento). Analogamente, i valori presenti sui fili "d0" e "d1" verranno "usati" dal modulo solo quando si verifica la condizione CS=1 e R/nW=0, ossia solo quando il modulo stesso viene attivato per una operazione di scrittura. In generale potremo quindi rappresentare un generico modulo RAM organizzato in 2**k celle di m bit con lo schema:
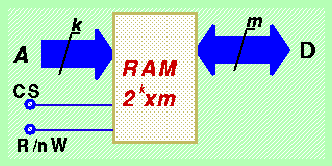
e questo potrà essere realizzato internamente usando lo schema di connessione illustrato.
Le memorie RAM statiche illustrate fino ad ora risolvono in linea di principio il problema di realizzare dei moduli RAM effettivamente usabili in pratica. Tuttavia l'attuale sviluppo della tecnologia di realizzazione dei dispositivi logici non consente di realizzare moduli RAM statici di dimensioni adeguate alle esigenze degli utilizzatori. Un rapido calcolo ci permette di trovare il limite superiore al numero di bit di ciascun modulo dato il massimo numero di componenti elettronici integrabili in un singolo dispositivo. I dispositivi RAM sono estremamente regolari e pertanto "facili" da realizzare, e l'attuale tecnologia consente di assemblare in uno stesso modulo fino ad un centinaio di milioni di "transistors" in casi come questo. Tuttavia occorrono una decina di transistor per realizzare una funzione logica elementare di tipo AND o OR, e si può valutare approssimativamente che occorrerebbero una decina di funzioni logiche elementari per ogni bit contenuto in un modulo di memoria RAM statica. Di conseguenza, si ricava un limite superiore per la dimensione dei moduli RAM statici dell'ordine di 1Mb. Un normale Personal Computer con 32MB di RAM richiederebbe quindi l'uso di almeno 256 moduli da 1Mb per la realizzazione della memoria usando l'approccio "statico".
L'alternativa economicamente più vantaggiosa consiste nell'abbandonare l'idea di realizzare i moduli RAM con la tecnica dei circuiti sequenziali, e sfruttare invece dei fenomeni elettromagnetici quali l'effetto "capacitivo" per memorizzare informazioni per una quantità di tempo limitata. Sfruttando l'effetto capacitivo dei "transistor ad effetto di campo" si riesce infatti a memorizzare un bit di informazione utilizzando pochissimi transistor. Il prezzo da pagare per questo risparmio in complessità realizzativa é che il valore inserito in una cella di memoria resta "memorizzato" solo per una quantità di tempo relativamente breve (frazioni di secondo), dopo di che viene "dimenticato" irrimediabilmente. L'idea che consente di realizzare dei moduli RAM "dinamici" consiste nel "rinfrescare la memoria" al dispositivo appena prima che il valore memorizzato vada perso. L'operazione di refresh di una memoria dinamica avviene leggendo il contenuto e riscrivendo immediatamente lo stesso valore appena letto, in modo che questo possa essere mantenuto per una ulteriore frazione di secondo. L'operazione di refresh deve essere ovviamente ripetuta periodicamente per tutti i bit memorizzati in un modulo RAM, ed il ciclo di refresh di tutte le celle deve completarsi in un tempo inferiore al tempo necessario ad una cella per "dimenticare" il proprio contenuto.
Moduli RAM dinamici vengono prodotti già completi con la logica
necessaria a realizzare il refresh di tutte le celle, ed offrono una interfaccia
funzionalmente simile a quella che abbiamo definito per i moduli statici.
L'unica differenza percepibile da un utilizzatore tra un dispositivo RAM
statico ed un dispositivo RAM dinamico sarà il maggior tempo di accesso
al contenuto delle celle di quest'ultimo rispetto al primo, a causa dell'attesa
per il completamento delle operazioni di refresh.
In compenso un modulo dinamico può contenere un numero di bit molto
superiore ad un modulo statico a parità di complessità circuitale,
ed oggi (marzo 2006) si trovano regolarmente in commercio moduli RAM
dinamici con capacità di 512MB e 1GB.
In alternativa alla organizzazione di tipo RAM della memoria, dove le celle vengono individuate mediante il loro numero d'ordine (indirizzo), in molte circostanze risulterebbe utile poter disporre di un dispositivo in grado di individuare una cella sulla base di parte del suo contenuto. Un tale dispositivo che consente di realizzare in modo naturale una operazione di ricerca del contenuto viene detto memoria associativa. Per fissare le idee possiamo prendere come riferimento il problema dell'anagrafe tributaria, dove ciascuno di noi é identificato dal proprio codice fiscale, e dove uno può essere interessato a vedere tutte le informazioni relative ad una singola persona cercando tutte le informazioni che fanno riferimento in qualche modo a quel codice fiscale.
Il primo passo verso la realizzazione di una memoria di tipo associativo consiste quindi nel suddividere le informazioni contenute in una singola cella di memoria in due sottoinsiemi di bit: un primo sottoinsieme (normalmente chiamato "tag") che sarà soggetto alle ricerche di tipo associativo, ed un secondo sottoinsieme (normalmente detto "value") che codifica i valori ignoti che si stanno cercando. Le informazioni sono inserite in ordine qualsiasi all'interno di una memoria associativa, per cui l'unico modo per individuare la cella contenente il valore desiderato sarà quello di confrontare il contenuto del campo di ricerca (tag) di ciascuna cella col valore che interessa. La ricerca associativa vera e propria verrà quindi realizzata mediante un circuito comparatore di uguaglianza associato al campo tag di ciascuna cella. In figura é riportato uno schema realizzativo atto a supportare l'operazione di "lettura" delle celle di memoria associativa:
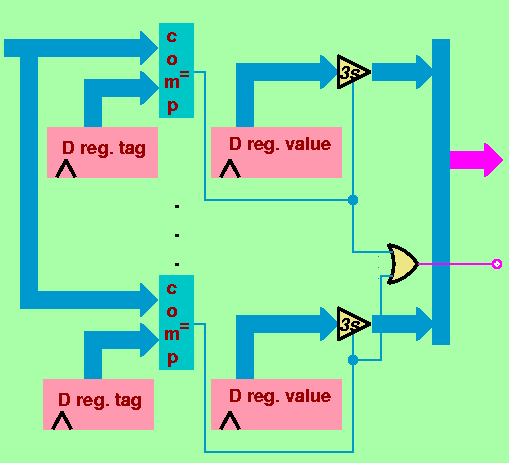
L'uscita dalla funzione OR calcola la condizione "almeno una cella contiene il valore cercato", mentre il valore (se l'uscita dell'OR vale 1) si trova sul bus di uscita. Per il corretto funzionamento dei dispositivi 3-s in uscita delle varie celle é necessario che non ci sia mai più di una cella contiene una certa combinazione di bit nel campo "tag" (se questa condizione é rispettata nessuna ricerca associativa potrà mai dare luogo a conflitti sul bus di uscita). Per poter garantire questa condizione é necessario che ciascuna operazione di scrittura di un nuovo valore sia preceduta da una ricerca associativa sul valore di tag che si vuole inserire: se quel valore di tag é già presente, allora occorre sostituire il vecchio valore col nuovo valore nella stessa cella; altrimenti (se il valore di tag che si vuole inserire non é già memorizzato in nessuna cella) occorre individuare una cella "vuota". Risulta quindi evidente la necessità di inserire almeno un ulteriore bit in ogni cella in modo da distinguere il caso di "cella vuota" da quello di "cella già contenente un valore". Nel caso poi si volesse inserire un nuovo valore partendo dalla condizione in cui nessuna cella é vuota, allora bisognerebbe definire una opportuna politica di cancellazione di celle già usate in precedenza per far spazio per nuove informazioni.
Si può quindi notare come, nel caso di una memoria associativa, l'operazione
di scrittura sia più difficile non solo da realizzare ma anche da definire
rispetto al caso della operazione di ricerca/lettura.
I dettagli di realizzazione della scrittura in una memoria associativa non ci
interessano nel caso generale: riprenderemo in parte l'argomento parlando di
alcune applicazioni particolari della memoria associativa, quali per esempio
la realizzazione di memorie Cache.
Ci accontentiamo di notare qui come una memoria associativa sia strutturalmente
molto più complessa di una memoria RAM destinata a contenere la
stessa quantità di informazioni.
Di conseguenza memorie associative (di modeste dimensioni) vengono usate solo
in quelle circostanze in cui la ricerca associativa possa dare dei grossi
vantaggi rispetto all'accesso ad una memoria di tipo RAM, in modo da giustificarne
il costo molto maggiore.