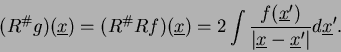Next: La filtered back projection
Up: Tecniche di ricostruzione tomografiche
Previous: Tecniche di ricostruzione tomografiche
Il Fourier slice theorem fornisce una relazione tra le proiezioni di una funzione
e la funzione stessa; esso afferma infatti che la trasformata di Fourier della proiezione
di f nella direzione 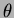 ha valori coincidenti con quelli
della trasformata di Fourier bidimensionale di f calcolata lungo la retta di direzione
ha valori coincidenti con quelli
della trasformata di Fourier bidimensionale di f calcolata lungo la retta di direzione
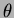 passante per l'origine dello spazio delle frequenze (fig. 3)
passante per l'origine dello spazio delle frequenze (fig. 3)
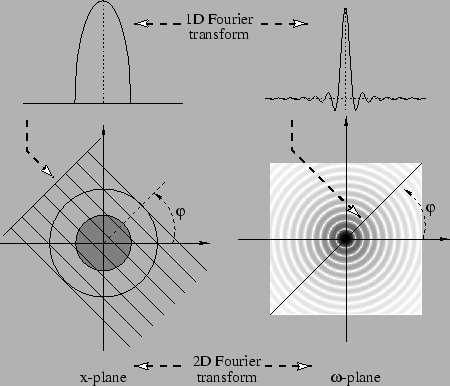
Figura 3:
Il Fourier slice theorem afferma che la trasformata di Fourier
della proiezione di f nella direzione 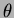 è
uguale alla trasformata di Fourier di f calcolata sulla
retta di direzione
è
uguale alla trasformata di Fourier di f calcolata sulla
retta di direzione 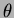 passante per l'origine dello
spazio delle frequenze.
passante per l'origine dello
spazio delle frequenze.
 |
Sia
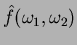 la trasformata di Fourier bidimensionale della
soluzione
la trasformata di Fourier bidimensionale della
soluzione 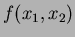 e
e
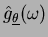 la trasformata di
Fourier di una proiezione
la trasformata di
Fourier di una proiezione
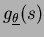 .
Possiamo scrivere:
.
Possiamo scrivere:
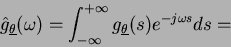 |
(14) |
Utilizzando le variabili 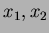 si ha:
si ha:
da cui
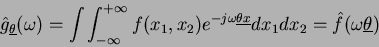 |
(15) |
Il significato di questo teorema, espresso dalla (16) è
il seguente: i valori della trasformata di Fourier della proiezione di 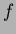 lungo la direzione
lungo la direzione
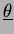 coincidono con i valori della trasformata
di Fourier di
coincidono con i valori della trasformata
di Fourier di 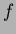 lungo la retta di direzione
lungo la retta di direzione
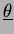 passante
per l'origine del piano
passante
per l'origine del piano
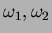 .
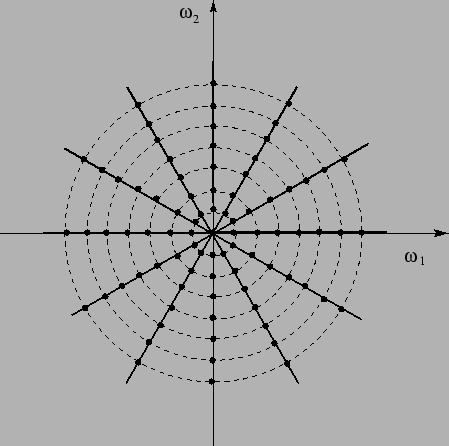
Il risultato precedente fornisce immediatamente un metodo per calcolare la
.
Il risultato precedente fornisce immediatamente un metodo per calcolare la
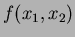 cercata: considerando le proiezioni per tutti gli angoli e facendone la trasformata di Fourier si possono determinare i valori di
cercata: considerando le proiezioni per tutti gli angoli e facendone la trasformata di Fourier si possono determinare i valori di
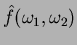 lungo linee radiali (fig. 4).
lungo linee radiali (fig. 4).
Figura:
Nel caso discreto il campionamento di
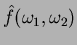 lungo
linee radiali causa perdita di precisione alle alte frequenze.
lungo
linee radiali causa perdita di precisione alle alte frequenze.
 |
Per ottenere la soluzione si può quindi applicare l'antitrasformata di
Fourier:
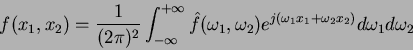 |
(16) |
Nella realtà è possibile effettuare solo un numero finito di proiezioni,
quindi, la trasformata di Fourier della 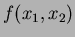 sarà nota solo su un numero
finito di linee radiali (come in fig. 4). Come sarà successivamente chiarito, per
applicare la (17) nel caso discreto, servono i valori di
sarà nota solo su un numero
finito di linee radiali (come in fig. 4). Come sarà successivamente chiarito, per
applicare la (17) nel caso discreto, servono i valori di
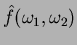 su di una griglia quadrata, i quali possono essere ottenuti tramite interpolazione dei
valori conosciuti; è però necessario notare che alle alte frequenze il
risultato di tale approssimazione sarà via via meno preciso, data la particolare
disposizione dei valori di
su di una griglia quadrata, i quali possono essere ottenuti tramite interpolazione dei
valori conosciuti; è però necessario notare che alle alte frequenze il
risultato di tale approssimazione sarà via via meno preciso, data la particolare
disposizione dei valori di 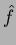 noti con esattezza.
noti con esattezza.
A questo punto è necessario definire l'operatore di retroproiezione, cioè
l'aggiunto di 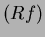 . Se indichiamo con
. Se indichiamo con  un generico elemento
dello spazio delle immagini e con
un generico elemento
dello spazio delle immagini e con 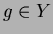 un elemento dello spazio delle proiezioni,
è possibile scrivere il prodotto scalare nello spazio
un elemento dello spazio delle proiezioni,
è possibile scrivere il prodotto scalare nello spazio 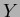 :
:
ovvero
se si sostituiscono le variabili 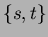 con
con 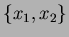 e si scambia
l'ordine di integrazione
e si scambia
l'ordine di integrazione
Quindi
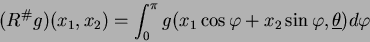 |
(17) |
E' interessante osservare che mentre la trasformata di Radon integra
sui tutti i punti di una retta, l'operatore di retroproiezione intrega su
tutte le rette che passano per un punto.
Se si applica l'operatore di retroproiezione ai dati si ottiene una
versione blurrata dell'oggetto.
Infatti si può dimostrare che



Next: La filtered back projection
Up: Tecniche di ricostruzione tomografiche
Previous: Tecniche di ricostruzione tomografiche
Patrizia Boccacci
2002-03-05