


Next: About this document ...
Up: Tecniche di ricostruzione tomografiche
Previous: Il Fourier slice theorem
Per evitare il ricorso all'interpolazione si affronta il problema in maniera totalmente diversa.
La formula di inversione della trasformata di Fourier
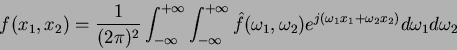 |
(18) |
utilizzando le coordinate polari definite da
può essere scritta come segue (
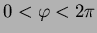 ,
,
 )
)
L'integrale su 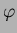 può essere diviso, considerando prima
può essere diviso, considerando prima 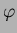 tra 0 e
tra 0 e  ,
poi
,
poi 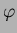 tra
tra  e
e 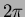 , e riscritto come segue
, e riscritto come segue
grazie alle proprietà della trasformata di Fourier
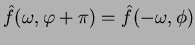 e
sostituendo
e
sostituendo  in
in 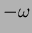 si ha
si ha
ovvero
![\begin{displaymath}
f(x_1,x_2)=\frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[ \int_{-...
...\omega(x_1\cos\varphi+x_2\sin\varphi)} d\omega\right] d\varphi
\end{displaymath}](img95.png) |
(21) |
Ricordando che, per la (16), vale
l'equazione precedente può essere riscritta nella seguente:
![\begin{displaymath}
f(x_1,x_2)=\frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[ \int_{-...
...\omega(x_1\cos\varphi+x_2\sin\varphi)} d\omega\right] d\varphi
\end{displaymath}](img95.png) |
(22) |
Nella (23) è presente un'operazione di filtraggio delle proiezioni, in cui
il filtro è rappresentato da 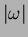 . Tale filtro è
detto a rampa,
amplifica le alte frequenze e con loro il rumore eventualmente presente sulle
proiezioni.
Poichè nella realtà non si verificano mai condizioni di assenza di rumore,
gli effetti sulla soluzione di questo filtraggio possono essere disastrosi. Per evitare
tale inconveniente vengono impiegati, assieme al
filtro a rampa, filtri passabasso (ad es. di Butterworth o di Hanning).
. Tale filtro è
detto a rampa,
amplifica le alte frequenze e con loro il rumore eventualmente presente sulle
proiezioni.
Poichè nella realtà non si verificano mai condizioni di assenza di rumore,
gli effetti sulla soluzione di questo filtraggio possono essere disastrosi. Per evitare
tale inconveniente vengono impiegati, assieme al
filtro a rampa, filtri passabasso (ad es. di Butterworth o di Hanning).
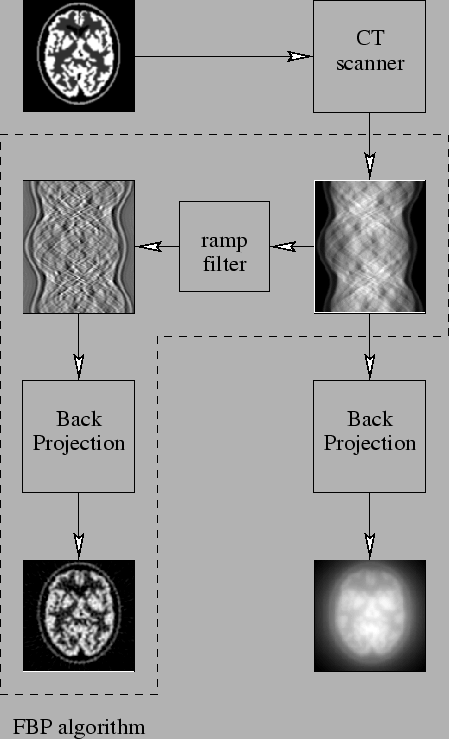
Figura 5:
Schema del procedimento base della Filtered Back Projection
 |



Next: About this document ...
Up: Tecniche di ricostruzione tomografiche
Previous: Il Fourier slice theorem
Patrizia Boccacci
2002-03-05
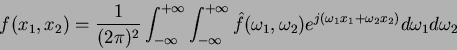
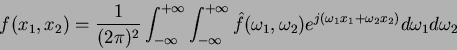
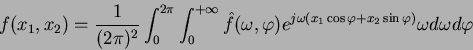
![$\displaystyle \frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[\int_0^{+\infty}\hat f(\om...
...hi)
e^{j\omega(x_1\cos\varphi+x_2\sin\varphi)} \omega d\omega\right] d\varphi +$](img88.png)
![$\displaystyle \frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[ \int_0^{+\infty}\hat f(\o...
...mega(x_1\cos(\varphi+\pi)+x_2\sin(\varphi+\pi))} \omega d\omega\right] d\varphi$](img90.png)
![$\displaystyle \frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[\int_0^{+\infty}\hat f(\om...
...hi)
e^{j\omega(x_1\cos\varphi+x_2\sin\varphi)} \omega d\omega\right] d\varphi +$](img88.png)
![$\displaystyle \frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[ \int_{-\infty}^0\hat f(\o...
...phi)
e^{j\omega(x_1\cos\varphi+x_2\sin\varphi)} -\omega d\omega\right] d\varphi$](img94.png)
![\begin{displaymath}
f(x_1,x_2)=\frac{1}{(2\pi)^2}\int_{0}^{\pi}
\left[ \int_{-...
...\omega(x_1\cos\varphi+x_2\sin\varphi)} d\omega\right] d\varphi
\end{displaymath}](img95.png)