Le tecniche a raggi-X classiche (radiografia) producono la registrazione fotografica bidimensionale (sulla lastra) dell'ombra proiettata da un cono di radiazione che attraversa un oggetto tridimensionale (corpo umano).
Le immagini prodotte in questo modo contengono informazioni sovrapposte da strutture che si trovano a differenti profondità nell'oggetto.
La Tomografia Assiale Computerizzata (TAC) permette, attraverso l'elaborazione dell'informazione, la ricostruzione della densità del corpo in esame, in sezioni (bidimensionali) perpendicolari all'asse del sistema di acquisizione.
Vediamo, innanzi tutto di descrivere il processo fisico che sta alla base
delle misure tomografiche.
Supponiamo di avere un emettitore di raggi-X (tipicamente con energie
comprese tra 20 e 150 Kev) che emette N fotoni (monocromatici) per unità di
tempo. Il fascio attraversa uno strato di materiale (biologico) di spessore ![]() .
Un rivelatore posto all'uscita del campione misurerà
.
Un rivelatore posto all'uscita del campione misurerà
![]() fotoni.
Infatti la radiazione X ha interagito con il tessuto e il fascio é stato attenuato.
fotoni.
Infatti la radiazione X ha interagito con il tessuto e il fascio é stato attenuato.
Nell'intervallo di frequenza tipico utilizzato per le immagini tomografiche, le cause di
questo assorbimento sono principalmente due: l'effetto fotoelettrico e l'effetto Compton.
Nel primo caso il fotone cede energia, nel secondo viene deviato dalla sua traiettora originale.
Questo fenomeno si può rappresentare con un unico coefficiente ![]() , detto di attenuazione,
e si scrive
, detto di attenuazione,
e si scrive
| (1) |
| (2) |
| (3) |
| (4) |
In generale il coefficiente ![]() non è uniforme ed è legato alla densità dei tessuti.
non è uniforme ed è legato alla densità dei tessuti.
Siano ![]() le coordinate cartesiane che individuano un piano dove giace una generica sezione
trasversale del corpo in esame e sia
le coordinate cartesiane che individuano un piano dove giace una generica sezione
trasversale del corpo in esame e sia ![]() la funzione (di due variabili) che rappresenta
in ogni punto il coefficiente di attenuazione, allora si può scrivere:
la funzione (di due variabili) che rappresenta
in ogni punto il coefficiente di attenuazione, allora si può scrivere:
| (5) |
Se ripetiamo ora la misura per un insieme di raggi paralleli, si può definire la proiezione dell'oggetto nella direzione di L e tale proiezione può essere vista come una funzione unidimensionale della posizione del rivelatore. Formalizziamo ora la definizione con l'aiuto delle notazioni schematizzate in figura 2.
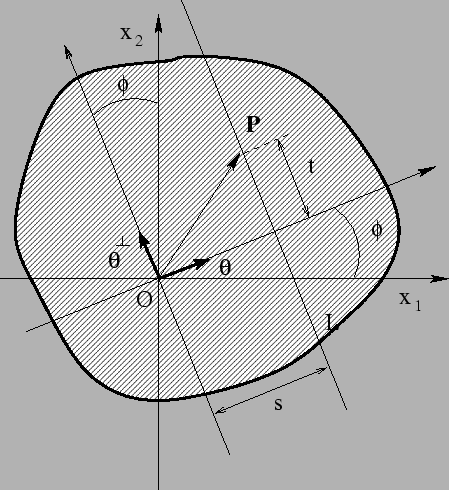 |
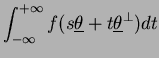 |
(6) | ||
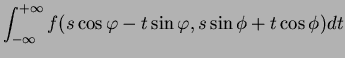 |
| (7) |
La trasformata di Radon ha una proprietà di simmetria che ci permette di far variare
![]() solo nel'intervallo
solo nel'intervallo ![]() :
:
| (8) |
Come si può facilmente intuire, nella pratica, la traformata di Radon è nota (misurata)
solo su un numero finito di rette (direzioni) e su un numero finito di punti per direzione.
L' insieme dei dati raccolti dai rivelatori in ogni direzione è detto (nel caso discreto)
sinogramma.
Il problema della tomografia si riconduce quindi alla ricerca della
funzione ![]() dalle sue proiezioni
dalle sue proiezioni
![]() , ovvero risolvere la seguente
equazione:
, ovvero risolvere la seguente
equazione:
| (9) |
Radon, nel 1917, diede una soluzione analitica della (13):
Nel seguito verrà illustrata la tecnica di Filtered Back Projection
che, basandosi sul teorema di Fourier, permette di ottenere una ricostruzione
dei dati sperimentali.